These NCERT Solutions for Class 8 Maths Chapter 16 Playing with Numbers Ex 16.1 Questions and Answers are prepared by our highly skilled subject experts.
NCERT Solutions for Class 8 Maths Chapter 16 Playing with Numbers Exercise 16.1
Question 1.
Find the values of the letters in each of the following and give reasons for the steps involved.
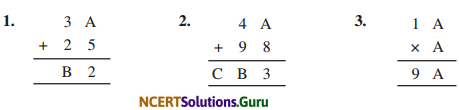

Answer:
1. Let us see the sum in units column. It is A + 5 and we get 2 from this
(A+ 5 = 7 + 5= 12). So, A has to be 7
For sum in ten’s column, we have
1 + 3 + 2 = B
∴ B = 6
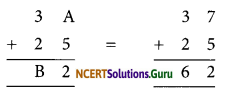
![]()
Question 2.
Here, there are three letters A, B and C whose values are to be found out.
Answer:
Let us see the sums in units column.
It is A + 8 and we get 3 from that so A has to be 5 (A + 8 = 5 + 8 = 13)
Now, for the sum in tens column, we have
I + 4 + 9= 14
∴ B = 4, C = 1
∴ The given puzzle is solved,
i. e. A = 5, B = 4 and C = 1
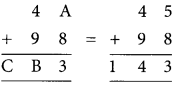
Question 3.
Units digit of A x A is A
Answer:
∴ A = 1 or 5 or 6
When, A = 1
II ≠ 9A
∴ A ≠ 1
When, A = 5
15 x 5 ≠ 9A;
∴ A ≠ 5
When, A = 6
16 x 6 = 96
∴ A = 6
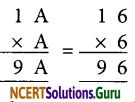
![]()
Question 4.
Here, there are two letters A and B whose values are to be found out.
Answer:
B + 7 gives A
and A + 3 gives 6
The possible values are 0 + 7 = 7
A = 7 but 7 + 3 ≠ 6 so it is not acceptable.
1 + 7 = 8
A = 8 but 8 + 3 ≠ 6 so not acceptable
2 + 7 = 9
A = 9 but 9 + 3 ≠ 6 so not acceptable
3 + 7= 10
A = 0 but 1+0 + 3 ≠ 6 so, not acceptable.
4 + 7= 11
A = 1 but 1 + 1 + 3 ≠ 6 so not acceptable.
5 + 7= 12
A = 2 Also 1 + 2 + 3 = 6
So B = 5 works and then we get A as 2
∴ the puzzle is solved as shown below
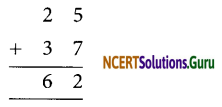
i. e. A = 2 and B = 5.
5. We need B x 3 = □ B
Since 5 x 3 = 15
∴ Possible value of B can be 5.
Also 0 x 3 = 0, i.e., B = 0 can be another possible value
∵ A x 3 = A + 0 = A
∴ Possible value of A = 5 or A = 0
∴ Since C ≠ 0
∴ Possible value of A = 5
30, B must be
Thus, B = 0.
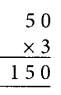
6. B can be either 5 or 0.
∵ A x 5 = A
∴ B must be 0
Again A can either 5 or 0
∴ C ≠ 0
∴ A ≠ 0
∴ A must be equal to 5
Thus, we have
Therefore, A = 5, B = 0, C = 2
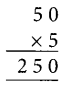
7. B can be 2, 4, 6 or 8
We need product 111 or 222, or 333 or 444 or 888 out of them 111 and 333 are rejected Possible products are 222, 444 or 888 To obtain
The possible value is B = 4
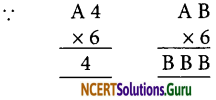
∴ A can be either 2 or 7
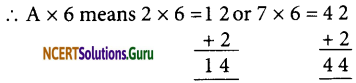
∴ A x 6 = 7 x 6 is the accepted value
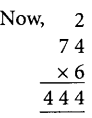
Thus, A = 7 and B = 4
![]()
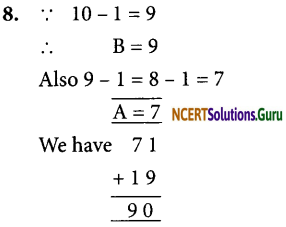
Thus, A = 7 and B = 9
9. ∵ 8 – 1 = 7
∴ B = 7
7 + 4= 11 ∴ A = 4
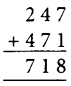
Now, we have
Thus A = 4 and B = 7
10. 10 – 2 = 8
∴ A = 8
Also 9 – 8 = 1
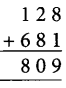
∴ B = 1
Now, we have
Thus, A = 8 and B = 1