These NCERT Solutions for Class 8 Maths Chapter 16 Playing with Numbers InText Questions and Answers are prepared by our highly skilled subject experts.
NCERT Solutions for Class 8 Maths Chapter 16 Playing with Numbers InText Questions
NCERT Intext Question Page No. 250
Question 1.
Write the following numbers in generalised form.;
(i) 25
(ii) 73
(iii) 129
(iv) 302
Answer:
(i) 25 = 20 + 5 = 2 × 10 + 5 × 1 = 10 × 2 + 5
(ii) 73 = 70 + 3 = 7 × 10 + 3 × 1 = 10 × 7 + 3
(iii) 129 = 100 + 20 + 9
= 1 × 100 + 2 × 10 + 9 × 1
= 100 × 1 + 10 × 2 + 9
(iv) 302 = 3 × 100 + 0 × 10 + 2 × 1
= 100 × 3 + 10 × 0 + 2
![]()
Question 2.
Write the following in the usual form.
(i) 10 × 5 + 6
(ii) 100 × 7 + 10 × 1 + 8
(iii) 100 × a + 10 × c + b
Answer:
(i) 10 × 5 + 6 = 50 + 6 = 56
(ii) 100 × 7 + 10 × 1 + 8
= 700 + 10 + 8 = 718
(iii) 100 × a + 10 × c + b
= 100a + 10c + b = a c b
NCERT Intext Question Page No. 257
Question 1.
If the division N + 5 leave a remainder of 3, what might be the one’s digit of N?
Answer:
The unit digit when divided by 5 must leave a remainder of 3.50, the one’s digit must be either 3 or 8.
Question 2.
If the division N + 5 leaves a remainder of 1, what might be the ones digit of N?
Answer:
The one’s digit when divided by 5 must have a remainder of 1. So the one’s digit must be either 1 or 6.
Question 3.
If the division N + 5 leaves a remainder of 4. What might be the one’s digit of N?
Answer:
The one’s digit, when divided by 5 must leave a remainder of 4. So the one’s digit must be either 4 or 9.
![]()
NCERT Intext Question Page No. 259
Question 1.
Check the divisiblity of the following number by 9.
(i) 108
(ii) 616
(iii) 294
(iv) 432
(v) 927
Answer:
(i) 108
Sum of the digits = 1 + 0 + 8 = 9 which is divisible by 9.
∴ 108 is divisible by 9.
(ii) 616
Sum of the digits = 6 + 1 + 6
= 13 which is not divisible by 9.
∴ 616 is not divisible by 9.
(iii) 294
Sum of the digits = 2 + 9 + 4 = 15
which is not divisible by 9.
∴ 294 is not divisible by 9.
(iv) 432
Sum of the digit = 4 + 3 + 2 = 9
which is divisible by 9.
∴ 432 is divisible by 9.
(v) 927
Sum of the digits = 9 + 2 + 7 = 18
which is divisible by 9.
∴ 927 is divisible by 9.
![]()
Question 9.
Check the divisibility of the following number by 3.
(i) 108
(ii) 616
(iii) 294
(iv) 432
(v) 927
Answer:
(i) 108
Sum of the digits =1 + 0 + 8 = 9
which is divisible by 3.
∴ 108 is divisible by 3.
(ii) 616
Sum of the digits = 6 + 1 + 6 = 13
which is not divisible by 3.
∴ 613 is also not divisible by 3.
(iii) 294
Sum of the digits = 2 + 9 + 4 = 15
which is divisible by 3.
∴ 294 is also divisible by 3.
(iv) 432
Sum of the digits = 4 + 3 + 2 = 9
which is divisible by 3.
∴ 432 is also divisible by 3.
(v) 927
Sum of the digits = 9 + 2 + 7 = 18 which is divisible by 3.
∴ Thus 927 is also divisible by 3.
![]()
NCERT Intext Question Page No. 251
Question 1.
Check what the result would have been if Sundaram had chosen the numbers shown below.
1. 27
2. 39
3. 64
4. 17
Answer:
1. Chosen number = 27
Number with reversed digits = 72
Sum of the two numbers = 27 + 72 = 99
Now, 99 = 11 [9] = 11 [2 + 7]
= 11 [Sum of the digits of the chosen number]
2. Chose number = 39
Number with reversed digits = 93
Sum of the two numbers = 39 + 93 = 132
Now, 132 ÷ 11 = 12
i. e„ 132 = 11 [12] = 11 [3 + 9]
= 11 [Sum of the digits of the chose number]
3. Chosen number = 17
Number with reversed digits = 71
Sum = 17 + 71 = 88
Now, 88 = 11 [8] = 11 [1 + 7]
= 11 [Sum of the digits of the chosen number]
Question 2.
Check what the result would have been if Sundaram had chosen the numbers shown.
1. 17
2. 21
3. 96
4. 37
Answer:
1. Chosen number =17
Number with reversed digits = 71
Difference = 71 – 17 = 54 = 9 × [6]
= 9 x [Difference of the digits of the chosen number (7 – 1 = 6)]
![]()
2. Chosen number = 21
Number with reversed digits = 12
Difference = 21 – 12 = 9 = 9 × [1]
= 9 x [Difference of the digits of the chosen number (12 -1 = 1)]
3. Chosen number = 96
Number with reversed digits = 69
Difference = 96 – 69 = 27 = 9 × [3]
=9 x [Difference of the digits of the chosen number (9 – 1 = 3)]
4. Chosen number = 37
Number with reversed digits = 73
Difference = 73 – 37 = 36 = 9 × [4]
=9 x [Difference of the digits of the chosen number (7-3 = 4)]
NCERT Intext Question Page No. 252
Question 1.
Check what the result would have been if Minakshi had chosen the numbers shown below. In each case keep a record of the quotient obtained at the end.
1. 132
2. 469
3. 737
4. 901
Answer:
1. 132 Chosen number = 132
Reversed number = 231
Difference = 231 – 132 = 99
We have 99 ÷ 99 = 1, remainder = 0
2. 469 Chosen number = 469
Reversed number = 964
Difference = 964 – 469 = 495
We have 99 ÷ 99 = 5, remainder = 0
3. Chosen number = 737
Reversed number = 737
We have Difference = 737 – 737 = 0
0 ÷ 99 =0, remainder = 0
4. Chosen number = 901
Reversed number = 109
Difference = 901 – 109 = 792
We have 792 ÷ 99 = 8, remainder = 0
Forming three-digit number with given three digits
NCERT Intext Question Page No. 253
Question 1.
Check what the result would have been if Sundaram had chosen the numbers shown below.
1. 417
2. 632
3. 117
4. 937
Answer:
1. Chosen number = 417
Two other numbers with the same digits are 741 and 174
Sum of the three numbers
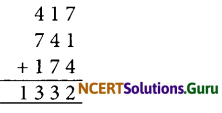
We have 1332 ÷ 37 = 36, remainder = 0
2. Chosen number = 632
Two other numbers are 263 and 326
Sum of the three numbers
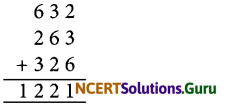
We have 1221 ÷ 37 = 33, remainder = 0
![]()
3. Chosen number =117
Other numbers are 711 and 171
Sum of the three numbers
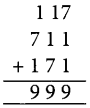
We have 1221 ÷ 37 = 33, remainder = 0
4. Chosen number = 937
Other two numbers are 793 and 379
Sum of the three numbers

We have 2109 + 37 = 57, remainder = 0