Math is tough but solving them is impossible said no one ever!! Make use of these NCERT Solutions For Class 10 Maths for finding solutions and also note that NCERT Solutions for Class 10 Maths PDF are available online for extra reference. This chapter includes NCERT Solutions for Class 10 Maths Chapter 2 Polynomials Ex 2.4. Practice more so you score more!!
NCERT Solutions for Class 10 Maths Chapter 2 Polynomials
Exercise 2.4
Question 1.
Verify that the numbers given alongside of the cubic polynomials below are their zeroes. Also, verify the relationship between the zeroes and the coefficients in each case:
(i) 2x3 + x2 – 5x + 2; \(\frac { 1 }{ 2 }\), 1, – 2
(ii) x3 – 4x2 + 5x – 2; 2, 1, 1
Solution:
(i) Comparing the given polynomial with ax3 + bx2 + cx + d, we get:
a = 2, b – 1, c = -5 and d = 2.
Now, we get the zeroes
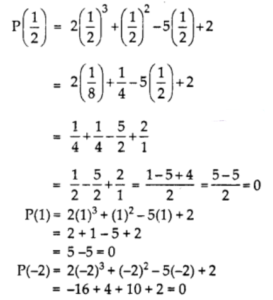
Therefore, \(\frac { 1 }{ 2 }\), 1, – 2 are the zeroes of 2x³ + x² – 5x + 2.
So we take α, ß, γ are the co-efficient of cubic polynomial.
Sum of zeroes

(ii) x3 – 4x2 + 5x – 2; 2, 1, 1
Compearing the given polynomial with ax3 + bx2 + cx + d, we get:
a = 1, b = -4, c = 5 and d = – 2.
∴ p (x) = x3 – 4x2 + 5x – 2
⇒ p(2) = (2)3 – 4(2)2 + 5 x 2 – 2
= 8 – 16+ 10 – 2 = 0
p(1) = (1)3 – 4(1)2 + 5 x 1- 2
= 1 – 4 + 1 – 2
= 6 – 6 = 0
Therefore, 2, 1 and 1 are the zeroes of x3 – 4x2 + 5x – 2.
So, take α, ß, γ are the coefficient of cubic polynomial.
Comparing x² – 4x² + 5x – 2 = 0
Sum of zeroes

Question 2.
Find a cubic polynomial with the sum, sum of the product of its zeroes taken two at a time, and the product of its zeroes as 2, -7, -14 respectively.
Solution:
We know that a cubic equation is ax³ + bx² + cx + d = 0
But given, α + β + γ = 2
αβ + βγ + γα = -7 and αβγ = – 14
Also, we know that a + b + g = \(\frac { -b }{ a }\) = 2, hence, b = – 2
αβ + βγ + γα = \(\frac { c }{ a }\) = – 7, hence c = – 7 a
αβγ = \(\frac { -d }{ a }\) = – 14, hence d = – 14, and a = 1
Now, put the value of a, b, c, d in equation (1), we get
x³ – 2x² – 7x + 14 = 0
Question 3.
If the zeroes of the polynomial x3 – 3x2 + x + 1 are a-b, a, a + b, find a and b.
Solution:
Zeroes of the polynomial are a-b, a, a + b
Sum of zeroes = a-b + a + a + b = 3a

⇒ a³ – b²a = 1
Put a = 1, in a² – b²a = – 1
(1)³ – b² = – 1 ⇒ b² = 2
b= ± \(\sqrt{2}\)
values of a and b are 1, ± \(\sqrt{2}\)
Question 4.
If two zeroes of the polynomial x4 – 6x3 – 26x2 + 138x – 35 are 2 ± \(\sqrt{3}\), finnd other zeroes.
Solution:
Let two zeroes are 2 + \(\sqrt{3}\) and 2 – \(\sqrt{3}\),
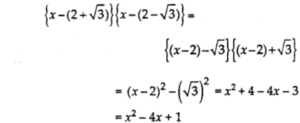
(x² – 4x +1) is a factor of the given polynomial.
Now, we divide the given polynomial by
So, x4 – 6x3 – 26x2 + 138x – 35 = (x2 – 4x + 1) (x2 – 2x – 35)
Now, by spilitting – 2x, we factorise x² – 2x – 35
= x3 – 7x + 5x – 35
= x(x – 7) (x + 5)
= (x – 7) (x + 5) px = 7, x = – 5
So, zeroes of the given polynomials are
2 + \(\sqrt{3}\), 2 – \(\sqrt{3}\), 7 and – 5.
Question 5.
If the polynomial x4 – 6x3 + 16x2 – 25x + 10 is divided by another polynomial x2 – 2x + k, the remainder comes out to be x + a, find k and a.
Solution:
If p(x) and g(x) are any two polynomials of the form x² – 2x and x² + bx + c. We know by formula.
Dividend = Divisor x Quotient + Remainder
x4 – 6x² + 16x3 – 25x + 10 = (x² – 2x + k) (x² + bx + c) + (x + a)
x4 – 6x3 + 16x² – 25x + 10 = x4 + bx3 + x²c – 2x3 – 2bx² – 2cx + kx² + kbx + kc + x + a
x4 – 6x3 + 16x² – 25x + 10 = x4 + (b – 2)x3 + (c – 2b + k) x² + (- 2x + kb + 1)x + kc + a
Now comparing the co-efficients of both sides b – 2 = – 6 … (1)
[Comparing the co-efficient of x3]
c – 2b + k = 16 … (2)
[Comparing the co-efficient of x²]
– 2c + kb + 1 = – 25 … (3)
[Comparing the co-efficient of x]
kc + a = 10 … (4)
[Comparing the constant term]
From (1), b = – 4
Now, putting the vlaue of b in equation (2) and (3) we get,
⇒ c – 2(- 4) + k = 16
or c + k = 8 … (5)
and -2c – 4k + 1 = – 25
or – 2c – 4k = – 26
or – c – 2k = – 13 … (6)
Adding equation (5) and (6), we get, c + k = 8
– c – 2k = – 13 – k = – 5
So, k = 5,
From (5), c = 8 – 5 ⇒ c = 3,
Now put the value of k and c in equation (4), we get,
kc + a = 10
5(3) + a = 10
a = – 5
∴ Value of k and a is 5 and – 5 respectively.
We hope you found these NCERT Solutions for Class 10 Maths Chapter 2 Polynomials Ex 2.4 helped you with finding the solutions easily.
Make sure to practice the remaining parts of the Class 10 Maths NCERT Solutions English Medium Chapter 2.