Math is tough but solving them is impossible said no one ever!! Make use of these NCERT Solutions For Class 10 Maths for finding solutions and also note that NCERT Solutions for Class 10 Maths PDF are available online for extra reference. This chapter includes NCERT Solutions for Class 10 Maths Chapter 2 Polynomials Ex 2.3. Practice more so you score more!!
NCERT Solutions for Class 10 Maths Chapter 2 Polynomials
Exercise 2.3
Question 1.
Divide the polynomial p(x) by the polynomial g(x) and find the quotient and remainder, in each of the following:
(i) p(x) = x3 – 3x2 + 5x -3, g(x) = x2-2
(ii) p(x) =x4 – 3x2 + 4x + 5, g(x) = x2 + 1 -x
(iii) p(x) = x4 – 5x + 6, g(x) = 2 -x2
Solution:
(i)
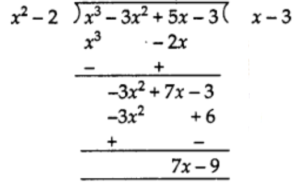
Therefore,
quotient = x – 3 and remainder = 7x – 9
(ii) First we arrange the terms of the dividend and the divisor in the decreasing order of their degrees.
∴ p(x) = x4– 3x2 + 4x + 5 and g(x) = x2 – x + 1
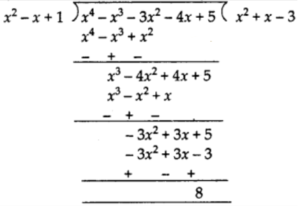
Therefore,
quotient = x2 +x-3 and remainder = 8
(iii) First we arrange the terms of the dividend and the divisior in the decreasing order of their degrees.
∴ p(x) = x2 + x – 3 and g(x) = – x2 + 2
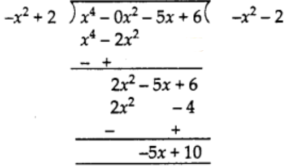
Therefore,
quotient = – x² – 2 and remainder = – 5x + 10
Question 2.
Check whether the first polynomial is a factor of the second polynomial by dividing the second polynomial by the first polynomial:
(i) t2 – 3, 2t4 + t3 – 2t2 – 9t – 12
(ii) x2 + 3x + 1, 3x4 + 5x3 -7x2 + 2x + 2
(iii) x3 – 3x + 1, x5 – 4x3 + x2 + 3x + l
Solution:
We have,
P(t) = 2t4 + 3t3 – 2t2 – 9t – 12
q(x) = t2 – 3
By actual division, we have

Here, remainder is zero.
Therefore, q(x) = t2 – 3 is the factor of p(x) = 2t4 + 3t3 – 2t2 – 9t – 12.
(ii) We have,
p(x) = 3x4 + 5x3 – 7x2 + 2x + 2
and q(x) = x² + 3x + 1
By actual division, we have
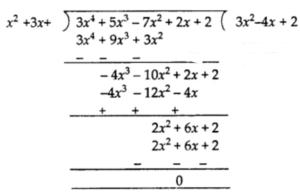
Here, remainder is not zero.
Therefore, q(x) = x² – 3x + 1 is not a factor of p(x) = 3x4 + 5x3 – 7x2 + 2x + 2.
(iii) We have,
p(x) = x5 – x3 + x2 + 3x + 1
and q(x) = x³ – 3x + 1
By actual division, we have
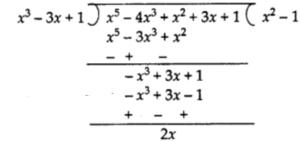
Here, remainder is not zero.
Therefore, q(x) = x² – 3x + 1 is not a factor of p(x) = x5 – x3 + x2 + 3x + 1.
Question 3.
Obtain all other zeroes of 3x4 + 6x3 – 2x2 – 10x – 5, if two of its zeroes are \(\sqrt { \frac { 5 }{ 3 } }\) and – \(\sqrt { \frac { 5 }{ 3 } }\)
Solution:
We have given that two zeroes of polynomial p(x) = 3x4 + 6x3 – 2x2 – 10x – 5 are \(\sqrt { \frac { 5 }{ 3 } }\) and – \(\sqrt { \frac { 5 }{ 3 } }\)
∴ (x – \(\sqrt { \frac { 5 }{ 3 } }\))(x + \(\sqrt { \frac { 5 }{ 3 } }\)) = x² – \(\frac { 5 }{ 3 }\) is a factor is given polynomial p(x).
Now apply the division algorithm to the given polynomial and x² – \(\frac { 5 }{ 3 }\)
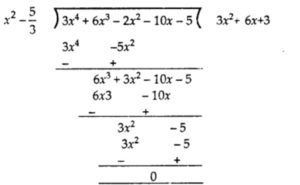
So, 3x4 + 6x3 – 2x2 – 10x – 5
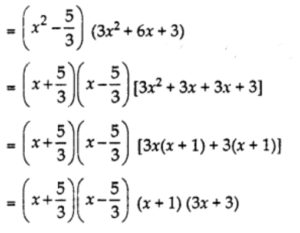
If 3x4 + 6x3 – 2x2 – 10x – 5 = 0
Then, (x + \(\sqrt { \frac { 5 }{ 3 } }\))(x – \(\sqrt { \frac { 5 }{ 3 } }\))(x + 1)(3x + 3) = 0
∴ x = \(\sqrt { \frac { 5 }{ 3 } }\) or x = \(\sqrt { \frac { 5 }{ 3 } }\) Therefore, the zeroes of polynomial p(x) = 3x4 + 6x3 – 2x2 – 10x – 5 are – \(\sqrt { \frac { 5 }{ 3 } }\), \(\sqrt { \frac { 5 }{ 3 } }\), -1 and -1.
Question 4.
On dividing x3 – 3x2 + x + 2 by a polynomial g(x), the quotient and remainder were x – 2 and – 2x + 4, respectively. Find g(x).
Solution:
We know that
Dividend = Divisor x Quotiet + Remainder
∴ x² – 3x² + x + 2 = g(x) x (x – 2) + (- 2x + 4)
or x3– 3x2 + x + 2 = g(x) (x – 2) + (-2x + 4)
or x3 – 3x2 + x + 2 + 2 x- 4 = g(x) x (x-2)
or x3 – 3x2 + 3x – 2 = g(x) x (x – 2)
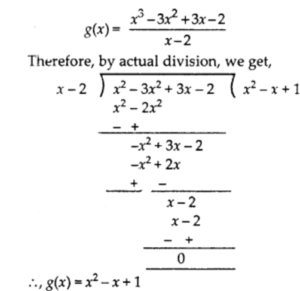
Question 5.
Give examples of polynomials p(x), g(x), q(x) and r(x), which satisfy the division algorithm and
(i) deg p(x) = deg q(x)
(ii) deg q(x) = deg r(x)
(iii) deg r(x) = 0
Solution:
(i) deg p(x) = deg q(x)
Polynomial p(x) = 2x2– 2x + 14; g(x) = 2
q(x) = x2 – x + 7 r(x) = 0
Here, deg p(x) = deg q(x)
(ii) deg q(x) = deg r(x)
Polynomial p(x) = x3+ x2 + x + 1; g(x) = x2 – 1,
q(x) = x + 1, r(x) = 2x + 2
(iii) deg r(x) is 0.
Polynomial p(x) = x2+ 2x2 – x + 2; g(x) = x2 – 1, q(x) = x + 1, r(x) = 4
We hope you found these NCERT Solutions for Class 10 Maths Chapter 2 Polynomials Ex 2.3 helped you with finding the solutions easily.
Make sure to practice the remaining parts of the Class 10 Maths NCERT Solutions English Medium Chapter 2.