Do you need some help in preparing for your upcoming Maths exam? We’ve compiled a list of MCQ Questions for Class 12 Maths with Answers to get you started with the subject, Determinants Class 12 MCQs Questions with Answers. You can download NCERT MCQ Questions for Class 12 Maths Chapter 4 Determinants with Answers Pdf free download and learn how smart students improve problem-solving skills well ahead. So, ace up your preparation with Class 12 Maths Chapter 4 Determinants Objective Questions.
Determinants Class 12 MCQs Questions with Answers
Don’t forget to practice the multitude of MCQ Questions of Determinants Class 12 with answers so you can apply your skills during the exam.
Question 1.
If \(\left|\begin{array}{rr}
x & 2 \\
18 & x
\end{array}\right|\) = \(\left|\begin{array}{rr}
6 & 2 \\
18 & 6
\end{array}\right|\), then x is equal to
(a) 6
(b) ±6
(c) -6
(d) 6, 6
Answer
Answer: (a) 6
Question 2.
Let A be a square matrix of order 3 × 3. Then |kA| is equal to
(a) k|A|
(b) k²|A|
(c) k³|A|
(d) 3k|A|
Answer
Answer: (c) k³|A|
Question 3.
Which of the following is correct?
(a) Determinant is a square matrix
(b) Determinant is a number associated to a matrix
(c) Determinant is a number associated to a square matrix
(d) None of these.
Answer
Answer: (c) Determinant is a number associated to a square matrix
Question 4.
If area of triangle is 35 sq. units with vertices (2, -6), (5, 4) and (k, 4). Then k is
(a) 12
(b) -2
(c) -12, -2
(d) 12, -2.
Answer
Answer: (d) 12, -2.
Question 5.
If A = \(\left[\begin{array}{lll}
a_{11} & a_{12} & a_{13} \\
a_{21} & a_{22} & a_{23} \\
a_{31} & a_{32} & a_{33}
\end{array}\right]\) and Aij is co-factors of aij, then A is given by
(a) a11A31 +a12A32 + a13A33
(b) a11A11 + a12A21 + a13A33
(c) a21A11 + a22A12 + a23A13
(d) a11A11 + a21A21 + a31A31
Answer
Answer: (d) a11A11 + a21A21 + a31A31
Question 6.
Let A be a non-singular matrix of order 3 × 3. Then |adj. A| is equal to
(a) |A|
(b) |A|²
(c) |A|³
(d) 3|A|
Answer
Answer: (b) |A|²
Question 7.
If A is any square matrix of order 3 x 3 such that |a| = 3, then the value of |adj. A| is?
(a) 3
(b) \(\frac { 1 }{3}\)
(c) 9
(d) 27
Answer
Answer: (c) 9
Question 8.
If A is an invertible matrix of order 2, then det (A-1) is equal to
(a) det (A)
(b) \(\frac { 1 }{det(A)}\)
(c) 1
(d) 0
Answer
Answer: (b) \(\frac { 1 }{det(A)}\)
Question 9.
If a, b, c are in A.P., then determinant
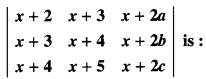
(a) 0
(b) 1
(c) x
(d) 2x
Answer
Answer: (a) 0
Question 10.
If x, y, z are non-zero real numbers, then the inverse of matrix A = \(\left[\begin{array}{lll}
x & 0 & 0 \\
0 & y & 0 \\
0 & 0 & z
\end{array}\right]\) is
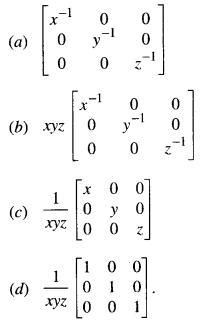
Answer
Answer:
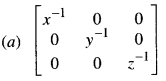
Question 11.
Let A = 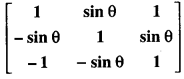
where 0 ≤ θ ≤ 2π then
(a) Det (A) = 0
(b) Det (A) ∈ (2, ∞)
(c) Det (A) ∈ (2, 4)
(d) Det (A) ∈ [2, 4]
Answer
Answer: (d) Det (A) ∈ [2, 4]
Question 12.
If \(\left|\begin{array}{rr}
2x & 5 \\
8 & x
\end{array}\right|\) = \(\left|\begin{array}{rr}
6 & -2 \\
7 & 3
\end{array}\right|\), then value of ‘x’ is
(a) 3
(b) ±3
(c) ±6
(d) 6
Answer
Answer: (c) ±6
Question 13.
Let Δ = \(\left|\begin{array}{lll}
\mathbf{A} x & x^{2} & 1 \\
B y & y^{2} & 1 \\
C z & z^{2} & 1
\end{array}\right|\) and Δ1 = \(\left|\begin{array}{rrr}
\mathbf{A} & \mathbf{B} & \mathbf{C} \\
\boldsymbol{x} & \boldsymbol{y} & z \\
z \boldsymbol{y} & z x & x y
\end{array}\right|\), then
(a) Δ1 = -Δ
(b) Δ ≠ Δ1
(c) Δ – Δ1 = 0
(d) None of these
Answer
Answer: (c) Δ – Δ1 = 0
Question 14.
If x, y ∈R, then the determinant:
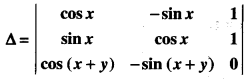
lies in the interval
(a) [-√2, √2]
(b) [-1, 1]
(c) [√2, 1]
(d) [-1, √2]
Answer
Answer: (a) [-√2, √2]
Question 15.
The area of a triangle with vertices (-3, 0), (3, 0) and (0, k) is 9 sq. units. The value of ‘k’ will be:
(a) 9
(b) 3
(c) -9
(d) 6.
Answer
Answer: (b) 3
Question 16.
If A, B and C are angles of a triangle, then the determinant:
\(\left|\begin{array}{ccc}
-1 & \cos C & \cos B \\
\cos C & -1 & \cos A \\
\cos B & \cos A & -1
\end{array}\right|\) is equal to
(a) 0
(b) -1
(c) 1
(d) None of these.
Answer
Answer: (a) 0
Question 17.
Let A be a square matrix all of whose entries are integers. Then which of the following is true?
(a) If det A = ± 1, then A-1 need not exist
(b) If det A = ± 1, then A-1 exists but all entries are not necessarily integers.
(c) If det A ≠ ± 1, then A-1 exists and all its entries are non-integers
(d) If det A = ± 1, then A-1 exists and all its entries are integers.
Answer
Answer: (d) If det A = ± 1, then A-1 exists and all its entries are integers.
Hint:
Since each entry of A is an integer,
∴ co-factor of each entry is also an integer.
Hence, each entry of the adjoint is an integer.
Also det A = ± 1 and A-1 = \(\frac { 1 }{det(A)}\) (adj A).
Hence, all entries of A-1 are integers.
Question 18.
The number of values of ‘k’ for which the linear equations:
4x + ky + 2z = 0
kx + 4y + z = 0
2x + 2y + z = 0
possesses a non-zero solution is
(a) 3
(b) 2
(c) 1
(d) zero.
Answer
Answer: (b) 2
Hint:
The system possesses non-zero solution
If \(\left|\begin{array}{lll}
4 & k & 2 \\
k & 4 & 1 \\
2 & 2 & 1
\end{array}\right|\) = 0
If 4(4 – 2) + k (k – 2) + 2(2k – 8) = 0
if = 8 – k² + 2k + 4k – 16 = 0
if k² – 6k + 8 = 0
if (k – 2)(k – 4) = 0
if k = 2 or 4
k = 2.
Question 19.
If A = \(\left[\begin{array}{lll}
1 & \alpha & 3 \\
1 & 3 & 3 \\
2 & 4 & 4
\end{array}\right]\) is the adjoint of a 3 × 3 matrix A and |A| = 4 then α is equal to
(a) 11
(b) 5
(c) 0
(d) 4
Answer
Answer: (a) 11
Hint:
Here |adj A| = |A|3-1
= |A|² = 4²
= 16
⇒ 1. (12 – 12) -α (4 – 6)+ 3(4 – 6) = 16
⇒ 2α – 6 = 16
⇒ 2α = 22.
Hence, α = 11.
Question 20.
If α, ß ≠ 0 and f(x) = α” + ß” and
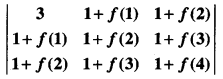
= k (1 – α)²(1 – ß)²(α – ß)², then ‘4k’ is equal to:
(a) \(\frac { 1 }{αß}\)
(b) 1
(c) -1
(d) αß
Answer
Answer: (b) 1
Hint:
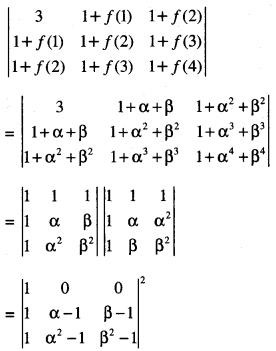
= [(α – 1) (ß² – 1) – (α² – 1) (ß – 1)]²
= (α – 1)²(ß – 1)²(α – ß)2.
Hence, k = 1
Question 21.
The system of linear equations:
x + λy – z = 0
λr – y – z = 0
x + y – λz = 0
has a non-trivial solution for
(a) Exactly one value of λ
(b) Exactly two values of λ
(c) Exactly three values of λ
(d) Infinitely many values of λ.
Answer
Answer: (c) Exactly three values of λ
Hint:
The system AX = O has non-trivial solution if det A = 0
i.,e if \(\left|\begin{array}{rrr}
1 & \lambda & -1 \\
\lambda & -1 & -1 \\
1 & 1 & -\lambda
\end{array}\right|\) = 0
⇒ (1)(λ + 1) -λ(-λ² + 1) + (-1)(λ + 1) = 0
⇒ λ + 1 + λ³ – λ – λ – 1 = 0
⇒ λ³ – λ = 0
⇒ λ(λ² – 1) = 0
⇒ λ = 0, 1, -1.
Hence, λ = -1, 0, 1.
Question 22.
Let on be a complex number such that 2ω + 1 = z, where z = √-3
If \(\left|\begin{array}{ccc}
1 & 1 & 1 \\
1 & -\omega^{2}-1 & \omega^{2} \\
1 & \omega^{2} & \omega
\end{array}\right|\) = 3k the k is equal to
(a) -1
(b) 1
(c) z
(d) -z
Answer
Answer: (c) z
Hint:
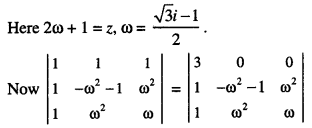
[Operating R1 → R1 + R2 + R3]
= 3[- ω (ω² + 1) – ω4]
= 3[- ω³ – ω – ω] = 3[- 1 – 2ω]
= – 3(1 + 2ω) = – 3z.
Thus 3k = – 3z.
Hence, k = -z.
Question 23.
If Sis the set of distinct values of ‘h’ for which the following system of linear equations:
x + y + z = 1,
x + ay + z = 1,
ax + by + z = 1
has no solution, then S is
(a) a finite set containing two or more elements
(b) a singleton
(c) an empty set
(d) an infinite set.
Answer
Answer: (b) a singleton
Hint:
D = \(\left|\begin{array}{lll}
1 & 1 & 1 \\
1 & a & 1 \\
a & b & 1
\end{array}\right|\) = 0
⇒ a – 1
⇒ x + y + z = 1
and x + by + z = 0.
The planes are parallel
⇒ b = 1.
Hence, S is a singleton.
Question 24.
If A = \(\left[\begin{array}{rr}
2 & -3 \\
-4 & 1
\end{array}\right]\), then adj. (3A² + 12A) is equal to
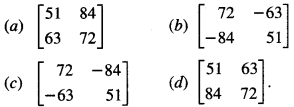
Answer
Answer:
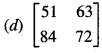
Hint:

Question 25.
If the system of linear equations:
x + ky + 3z = 0
3x + ky – 2z = 0
2x + 4y – 3z = 0
has a non zero solution (x, y, z), then \(\frac {xz}{y^2}\) is equal to:
(a) -10
(b) 10
(c) -30
(d) 30
Answer
Answer: (b) 10
Hint:
The given system has non-zero solution
⇒ \(\left|\begin{array}{ccc}
1 & k & 3 \\
3 & k & -2 \\
2 & 4 & -3
\end{array}\right|\)
⇒ 1(-3k + 8)-k (-9 + 4) + 3 (12 – 2k) = 0
⇒ 44 – 4k = 0
⇒ k = 11
Let z = λ
Thus x + 11 y = -3λ
and 3x + 11 y = 2λ
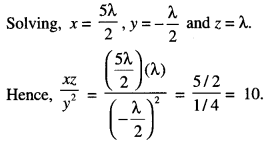
Fill in the blanks
Question 1.
If \(\left|\begin{array}{ll}
x & 2 \\
8 & x
\end{array}\right|\) = \(\left|\begin{array}{ll}
3 & 2 \\
9 & 6
\end{array}\right|\), then the value of x is ……………..
Answer
Answer: ±4
Hint:
\(\left|\begin{array}{ll}
x & 2 \\
8 & x
\end{array}\right|\) = \(\left|\begin{array}{ll}
3 & 2 \\
9 & 6
\end{array}\right|\)
⇒ x² – 16 = 18 – 18
⇒ x² = 16
⇒ x = ±4.
Question 2.
Let A be a 3 x 3 determinant and |A| = 7. Then the value of |2A| is ……………….
Answer
Answer: 56
Hint:
|2A| = 2³ |A| = 8 x 7 = 56.
Question 3.
If A = \(\left[\begin{array}{ll}
1 & 2 \\
4 & 2
\end{array}\right]\) Then the value of k = ……………
if |2A| = k|A|
Answer
Answer: 4
Hint:
if |2A| = 2²|A| = 4|A|
k = 4
Question 4.
If A is a skew-symmetric matrix of order 3, then det A = ……………..
Answer
Answer: 0.
Question 5.
The value of \(\left[\begin{array}{ccc}
102 & 18 & 36 \\
1 & 3 & 4 \\
17 & 3 & 6
\end{array}\right]\) is ……………..
Answer
Answer: 0
Hint:
Δ = 6\(\left|\begin{array}{ccc}
17 & 3 & 6 \\
1 & 3 & 4 \\
17 & 3 & 6
\end{array}\right|\) = 6(0) = 0
Question 6.
If Δ = \(\left|\begin{array}{ll}
1 & a \\
1 & b
\end{array}\right|\), then minor of ‘b’ is ………………
Answer
Answer: 1
Question 7.
Minor of ‘d’ is = \(\left|\begin{array}{ll}
a & c \\
b & d
\end{array}\right|\), is ………………
Answer
Answer: a
Question 8.
A square matrix A has inverse if and only if A is ………………
Answer
Answer: Invertible.
Question 9.
Co-factor of ‘b’ in \(\left|\begin{array}{ll}
a & c \\
b & d
\end{array}\right|\) is ……………
Answer
Answer: -c
Question 10.
If Δ = \(\left|\begin{array}{lll}
1 & 2 & 3 \\
2 & 0 & 1 \\
5 & 3 & 8
\end{array}\right|\) then minor of a22 is …………….
Answer
Answer: -7
We hope you found this NCERT MCQ Questions for Class 12 Maths Chapter 4 Determinants with Answers Pdf free download helpful. If you have any questions about CBSE Class 12 Maths Determinants MCQs Multiple Choice Questions with Answers, please share them in the comment box below and we will get back to you at the earliest possible time.