Do you need some help in preparing for your upcoming Maths exam? We’ve compiled a list of MCQ Questions for Class 12 Maths with Answers to get you started with the subject, Continuity and Differentiability Class 12 MCQs Questions with Answers. You can download NCERT MCQ Questions for Class 12 Maths Chapter 5 Continuity and Differentiability with Answers Pdf free download and learn how smart students improve problem-solving skills well ahead. So, ace up your preparation with Class 12 Maths Chapter 5 Continuity and Differentiability Objective questions.
Continuity and Differentiability Class 12 MCQs Questions with Answers
Don’t forget to practice the multitude of MCQ questions on Continuity and Differentiability Class 12 MCQs Questions with Answers so you can show your skills during the exam.
Question 1.
The function
f(x) = 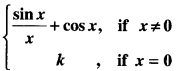
is continuous at x = 0, then the value of ‘k’ is:
(a) 3
(b) 2
(c) 1
(d) 1.5.
Answer
Answer: (b) 2
Question 2.
The function f(x) = [x], where [x] denotes the greatest integer function, is continuous at:
(a) 4
(b)-2
(c) 1
(d) 1.5.
Answer
Answer: (d) 1.5.
Question 3.
The value of ‘k’ which makes the function defined by
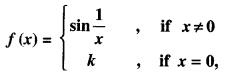
continuous at x = 0 is
(a) -8
(b) 1
(c) -1
(d) None of these.
Answer
Answer: (d) None of these.
Question 4.
Differential coefficient of sec (tan-1 x) w.r.t. x is
(a) \(\frac { x }{\sqrt{1+x^2}}\)
(b) \(\frac { x}{1+x^2}\)
(c) x\(\sqrt { 1+x^2}\)
(d) \(\frac { 1 }{\sqrt{1+x^2}}\)
Answer
Answer: (a) \(\frac { x }{\sqrt{1+x^2}}\)
Question 5.
If y = log (\(\frac { 1-x^2 }{1+x^2}\)) then \(\frac { dy }{dx}\) is equal to:
(a) \(\frac { 4x^3 }{1-x^4}\)
(b) \(\frac { -4x}{1-x^4}\)
(c) \(\frac {1}{ 4-x^4}\)
(d) \(\frac { -4x^3 }{1-x^4}\)
Answer
Answer: (b) \(\frac { -4x}{1-x^4}\)
Question 6.
If y = \(\sqrt { sin x+ y}\), then \(\frac { dy }{dx}\) is equal to
(a) \(\frac { cos x }{2y-1}\)
(b) \(\frac { cos x}{1-2y}\)
(c) \(\frac {sin x}{1-2y}\)
(d) \(\frac { sin x }{2y-1}\)
Answer
Answer: (a) \(\frac { cos x }{2y-1}\)
Question 7.
If u = sin-1 (\(\frac { 2x }{1+x^2}\)) and u = tan-1 (\(\frac { 2x }{1-x^2}\)) then \(\frac { dy }{dx}\) is
(a) \(\frac { 1 }{2}\)
(b) x
(c) \(\frac {1-x^2}{1+x^2}\)
(d) 1
Answer
Answer: (d) 1
Question 8.
If x = t², y = t³, then \(\frac { d^2y }{dx^2}\) is
(a) \(\frac { 3 }{2}\)
(b) \(\frac { 3 }{4t}\)
(c) \(\frac {3}{2t}\)
(d) \(\frac { 3t }{2}\)
Answer
Answer: (b) \(\frac { 3 }{4t}\)
Question 9.
The value of ‘c’ in Rolle’s Theorem for the function f(x) = x³ – 3x in the interval [0, √3] is
(a) 1
(b) -1
(c) \(\frac {3}{2}\)
(d) \(\frac {1}{3}\)
Answer
Answer: (a) 1
Question 10.
The value of ‘c’ in Mean Value Theorem for the function f(x) = x(x – 2), x ∈ [1, 2] is
(a) \(\frac {3}{2}\)
(b) \(\frac {2}{3}\)
(c) \(\frac {1}{2}\)
(d) \(\frac {3}{4}\)
Answer
Answer: (a) \(\frac {3}{2}\)
Question 11.
Let f : (- 1, 1) → R be a differentiable function with f(0) = – 1 and f'(0) = 1.
Let g(x) = [f (2f(x) + 2)]². Then g'(0) =
(a) 4
(b) -4
(c) log 2
(d) -log 2.
Answer
Answer: (b) -4
Hint:
Here g (x)= [f (2 f(x) + 2)]²
g'(x) = 2[f(2f(x) + 2)] \(\frac { d }{dx}\) [2f(x) + 2 ]
= 2f(2f(x) + 2) . [2 f'(x)]
∴ g'(0) = 2f(2f(0) + 2) . [2f'(0)]
= 2f(2 (-1) +2). 2f’/(0)
= 2f(0) . 2f'(0) = 4f(0) f'(0)
= 4 (-1) (1) = -4.
Question 12.
\(\frac { d^2x }{dy^2}\) equals
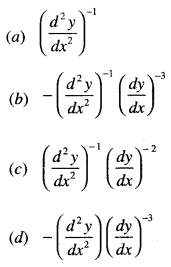
Answer
Answer: d
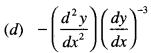
Hint:
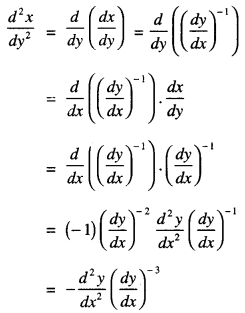
Question 13.
If function f(x) is differentiable at x = a, then
\(\lim _{x \rightarrow a}\) \(\frac { x^2 f(a) – a^2 f(x) }{x-a}\) is
(a) a² f(a)
(b) af(a) – a² f'(a)
(c) 2a f(a) – a² f'(a)
(d) 2a f (a) + a² f'(a).
Answer
Answer: (c) 2a f(a) – a² f'(a)
Hint:
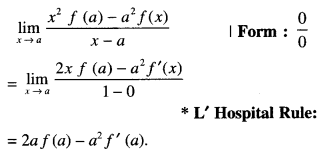
Question 14.
If f: R → R is a function defined by
f(x) = [x] cos (\(\frac { 2x-1 }{2}\))π, where [x] denotes the greatest integer function, then ‘f’ is
(a) continuous for every real x
(b) discontinuous only at x = 0
(c) discontinuous only at non-zero integral values of x
(d) continuous only at x = 0.
Answer
Answer: (a) continuous for every real x
Hint:
Continuous for every real x.
Question 15.
If y = sec (tan-1 x), then \(\frac { dy }{dx}\) at x = 1 is equal to
(a) \(\frac {1}{2}\)
(b) 1
(c) √2
(d) \(\frac {1}{√2}\)
Answer
Answer: (d) \(\frac {1}{√2}\)
Hint:
Here y = sec (tan-1 x).
∴ \(\frac { dy }{dx}\) = sec (tan-1 x) tan (tan-1 x). \(\frac { 1 }{1+x^2}\)
= sec (tan-1 x). x . (tan-1 x). \(\frac { 1 }{1+x}\)
\(\left.\frac{d y}{d x}\right]_{x=1}\) = sec (tan-1 1). \(\frac { 1 }{1+1}\)
= sec (\(\frac { π }{4}\)) \(\frac { 1 }{2}\) = \(\frac { √2 }{2}\) = \(\frac { 1 }{√2}\)
Question 16.
If g is the inverse of a function f and f'(x) = \(\frac { 1 }{1+x^5}\), then g'(x) is equal to
(a) 5x4
(b) \(\frac {1}{1+{g(x)}^5}\)
(c) 1 + {g(x)}5
(d) 1 + x5
Answer
Answer: (b) \(\frac {1}{1+{g(x)}^5}\)
Hint:
Here f(g(x)) = x. [∵ g is the inverse of f]
f'(g(x)) g'(x) = 1
⇒ g'(x) = \(\frac { 1 }{f'{g(x)}}\) = \(\frac { 1 }{1+{g(x)}^5}\)
Question 17.
If the function
g(x) = \(\left\{\begin{array}{ll}
k \sqrt{x+1} & ; 0 \leq x \leq 3 \\
m x+2 & ; 3 \end{array}\right.\)
is differentiable, then the value of k + m is
(a) 2
(b) \(\frac {16}{5}\)
(c) \(\frac {10}{3}\)
(d) 4
Answer
Answer: (a) 2
Hint:
We have
g(x) = \(\left\{\begin{array}{ll}
k \sqrt{x+1} & ; 0 \leq x \leq 3 \\
m x+2 & ; 3 \end{array}\right.\)
When this function is differentiable, then it is continuous
⇒ \(\lim _{x \rightarrow 3^{-}}\) g(x) = \(\lim _{x \rightarrow 3^{+}}\) g(x) = g(3)
⇒ 2k = 3m + 2 = 2k
⇒ 2k = 3m + 2 ………… (1)
Also, LHD = \(\lim _{x \rightarrow 3^{-}}\) g(x) = \(\frac {k}{4}\)
RHD = \(\lim _{x \rightarrow 3^{+}}\) g(x) = m
∴ LHD = RHD k
⇒ \(\frac {k}{4}\) = m
Solving (1) and (2),
k = \(\frac {8}{5}\) and m = \(\frac {2}{5}\)
Hence, k + m = \(\frac {8}{5}\) + \(\frac {2}{5}\) = \(\frac {10}{2}\) = 2.
Question 18.
For x ∈ R, f(x) = |log 2 – sin x| and g(x) =f(f(x)), then
(a) g is not differentiable at x = 0
(b) g'(0) = cos (log 2)
(c) g'(0) = -cos (log 2)
(d) g is differentiable at x = 0 and g'(0) = – sin (log 2).
Answer
Answer: (b) g'(0) = cos (log 2)
Hint:
We have : f(x) = log 2 – sin x
and g(x) = f(f cos x)
= log 2 – sin (log 2 – sin x).
Since ‘g’ is the sum of two differentiable functions,
∴ g is differentiable.
g'(x) = 0 – cos (log 2 – sin x) (0 – cos x)
= cos (log 2 – sin x) cos x.
Hence, g’ (x) = cos (log 2).
Fill in the blanks
Question 1.
If f(x) = \(\left\{\begin{array}{c}
\frac{x^{2}-1}{x-1}, \text { when } x \neq 1 \\
k, \text { when } x=1
\end{array}\right.\) is continuous then the value of k = …………………
Answer
Answer: 2.
Question 2.
If f(x) = x + 7, and g(x) = x – 7, x ∈R, then \(\frac { d }{dx}\) (fog) (x) = ……………….
Answer
Answer: 1.
Question 3.
If 2x + 3y = sin x, then \(\frac { dy }{dx}\) = …………………..
Answer
Answer: \(\frac { cos x-2 }{3}\)
Question 4.
\(\frac { d }{dx}\) (cosec-1 x) = …………………
Answer
Answer: \(\frac { -1 }{|x|\sqrt{x^2-1}}\)
Question 5.
\(\frac { d }{dx}\) (\(\sqrt { e^{ \sqrt{x}} }\)) = …………………
Answer
Answer: \(\frac { 1 }{4√x}\) \(\sqrt { e ^{\sqrt{x}} }\)
Question 6.
If x = at², y = 2at, then \(\frac { dy }{dx}\) = ……………….
Answer
Answer: \(\frac { 1 }{t}\)
Question 7.
The derivative of xx w.r.t. x is.
Answer
Answer: xx (1 + log x).
Question 8.
If y = x² + 3x + 2, then \(\frac { d^2y }{dx^2}\) = ………………
Answer
Answer: 2.
Question 9.
Value of ‘c’ in Rolle’s Theorem for the function f(x) = x³ – 3x in [-√3, 0] is ……………..
Answer
Answer: c = -1.
Question 10.
Value of ‘c’ in LMV Theorem for f(x) = x² in [2, 4] is …………………
Answer
Answer: c = 3.
We hope you found this NCERT MCQ Questions for Class 12 Maths Chapter 5 Continuity and Differentiability with Answers Pdf free download helpful. If you have any questions about CBSE Class 12 Maths Continuity and Differentiability MCQs Multiple Choice Questions with Answers, please share them in the comment box below and we will get back to you at the earliest possible time.