These NCERT Solutions for Class 8 Maths Chapter 12 Exponents and Powers Ex 12.1 Questions and Answers are prepared by our highly skilled subject experts.
NCERT Solutions for Class 8 Maths Chapter 12 Exponents and Powers Exercise 12.1
Question 1.
Evaluate
(i) 3-2
(ii) (-4)-2
(iii) \(\left(\frac{1}{2}\right)^{-5}\)
Answer:
(i) 3-2 = \(\frac{1}{3^{2}}=\frac{1}{9}\)
(ii) (-4)-2 = \(\frac{1}{(-4)^{2}}=\frac{1}{16}\)
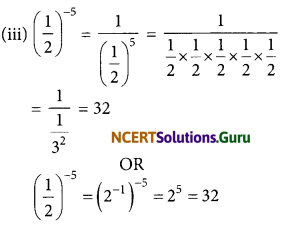
![]()
Question 2.
Simplify and express the result in power notation with positive exponent.
(i) (-4)5 ÷ (-4)8
(ii) \(\left(\frac{1}{2^{3}}\right)^{2}\)
(iii) (-3)4 × \(\left(\frac{5}{3}\right)^{4}\)
(iv) (3-7 ÷ 310) × 3-5
(v) 2-3 × (-7)-3
Answer:


Question 3.
Find the value of
(i) (3° + 4-1) × 22
(ii) (2-1 × 4-1) ÷ 2-2
(iii) \(\left(\frac{1}{2}\right)^{-2}+\left(\frac{1}{3}\right)^{-2}+\left(\frac{1}{4}\right)^{-4}\)
(iv) (3-1 + -1 + 5-1)0
(v) \(\left\{\left(\frac{-2}{3}\right)^{-2}\right\}^{2}\)
Answer:
(i) (3° + 4-1) × 22
= (1 + \(\frac{1}{4}\) ) × 22
[(i) a0 = 1 (ii) a-m = \(\frac{1}{a^{m}}\) ]
= \(\left(\frac{4+1}{4}\right)\) × 4 = \(\frac{5}{4}\) × 4 = 5
![]()
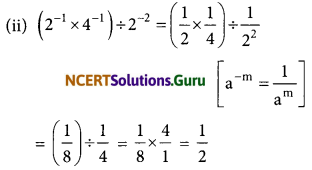

Question 4.
Evaluate:
(i) \(\frac{8^{-1} \times 5^{3}}{2^{-4}}\)
(ii) (5-1 × 2-1) × 6-1
Answer:
\(\frac{8^{-1} \times 5^{3}}{2^{-4}}=\frac{5^{3} \times 2^{4}}{8^{1}}=\frac{(5 \times 5 \times 5) \times 2^{4}}{2^{3}}\)
= 125 × 24-3 = 125 × 21 = 250
(ii) (5-1 × 2-1) × 6-1 = \(\left(\frac{1}{5} \times \frac{1}{2}\right) \times \frac{1}{6}\)
[a-m = \(\frac{1}{\mathrm{a}^{\mathrm{m}}}\) ]
= \(\frac{1}{10} \times \frac{1}{6}=\frac{1}{60}\)
Question 5.
Find the value of m for which 5m ÷ 5 3 = 55.
Answer:
5m ÷ 5-3 = 55
5m ÷ \(\frac{1}{5^{3}}\) = 55
5m × 53 = 55
5m+3 = 55 (am × an = am+n)
∴ m + 3 = 5 (since the bases are equal, the exponents are equal)
m = 5 – 3
m = 2
The value of m = 2.
Question 6.
Evaluate
(i) \(\left\{\left(\frac{1}{3}\right)^{-1}-\left(\frac{1}{4}\right)^{-1}\right\}^{-1}\)
(ii) \(\left(\frac{5}{8}\right)^{-7} \times\left(\frac{8}{5}\right)^{-4}\)
Answer:
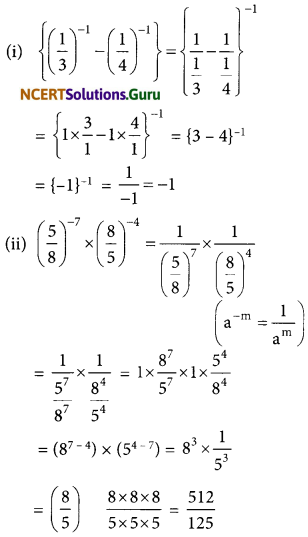
![]()
Question 7.
Simplify:
(i) \(\frac{25 \times \mathrm{t}^{-4}}{5^{-3} \times 10 \times \mathrm{t}^{-8}}(\mathrm{t} \neq 0)\)
(ii) \(\frac{3^{-5} \times 10^{-5} \times 125}{5^{-7} \times 6^{-5}}\)
Answer:
