These NCERT Solutions for Class 6 Maths Chapter 5 Understanding Elementary Shapes Ex 5.5 Questions and Answers are prepared by our highly skilled subject experts.
NCERT Solutions for Class 6 Maths Chapter 5 Understanding Elementary Shapes Exercise 5.5
Question 1.
Which of the following are models for perpendicular lines:
(a) The adjacent edges of a table top.
(b) The lines of a railway track.
(c) The line segments forming the letter ‘L’.
(d) The letter V.
Answer:
(a) The adjacent edges of a table top.
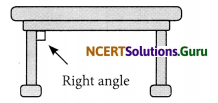
.’. They form perpendicular lines,
![]()
(b) The lines of a railway track
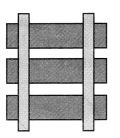
Here, the two adjacent sides don’t meet.
χ They do not form perpendicular lines
(c) The line segments forming the letter ‘L’.
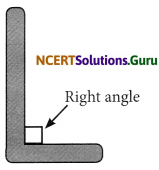
Here, the line segments form a right angle
∴ They form perpendicular lines.
(d) Here, the angle between the lines is not a right angle.
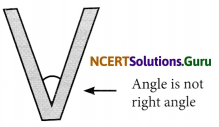
∴ They do not form perpendicular lines.
Question 2.
Let \(\overline{\mathrm{PQ}}\) be the perpendicular to the line segment \(\overline{\mathrm{XY}}\). Let \(\overline{\mathrm{PQ}}\) and \(\overline{\mathrm{XY}}\) intersect in the point A. What is the measure of ∠PAY?
Answer:
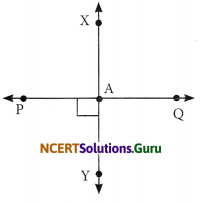
Since, \(\overline{\mathrm{XY}}\) ⊥ PQ
Angle between them is a right angle.
.’. ∠PAY = 90°
Question 3.
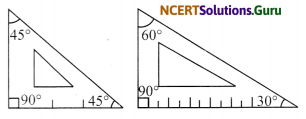
There are two set-squares in your box. What are the measures of the angles that are formed at their corners? Do they have any angle measure that is common?
Answer:
The angle are 90°, 45°, 45°
The angles are 90°, 60°, 30°
So, Angle 90° is common between them
![]()
Question 4.
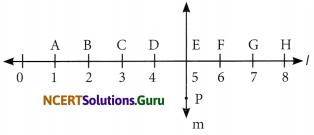
Study the diagram. The line l is perpendicular to line m.
(a) Is CE = EG?
(b) Does PE bisect CG?
(c) Identify any two line segments for which PE is the perpendicular bisector.
(d) Are these true?
(i) AC > FG (ii) CD = GH (iii) BC < EH
Answer:
(a) CE = CD + DE = 1 + 1=2 EG = EF + FG = 1 + 1 = 2
(b) PE & CG Intersect at point E & CE = EG
.’. PE is the bisector of CG
(c) PE is perpendicular bisector for
\(\overline{\mathrm{CG}}\)
As CE = EG = 2
& \(\overline{\mathrm{CE}}\) = EG = 2
\(\overline{\mathrm{XY}}\) ⊥ \(\overline{\mathrm{CG}}\)
\(\overline{\mathrm{BH}}\)
As \(\overline{\mathrm{BE}}=\overlline{\mathrm{BE}}\) = 3
\(\overline{\mathrm{PE}}=\overlline{\mathrm{BH}}\)
(d) (i) True
AC = AB + BC = 1 + 1 = 2
FG = 1
∴ AC > FG
(ii) True
CD = 1
GH = 1
CD > GH
![]()
(iii) True
BC = 1
EH = EF + FG + GH = 1 + 1 + 1 = 3
∴ CD > GH