These NCERT Solutions for Class 9 Maths Chapter 8 Quadrilaterals Ex 8.1 Questions and Answers are prepared by our highly skilled subject experts.
NCERT Solutions for Class 9 Maths Chapter 8 Quadrilaterals Exercise 8.1
Question 1.
The angles of a quadrilateral are in the ratio 3 : 5 : 9 : 13. the angles of the quadrilateral.
Solution:
Let the first angle of the quadrilateral be 3x.
Second angle of quadrilateral is 5x.
The third angle of the quadrilateral is 9x.
The fourth angle of the quadrilateral is 13x.
Therefore,
3x + 5x + 9x + 13x = 360 (sum of all four angles of a quadrilateral is 360)
⇒ 30x = 360
⇒ x = \(\frac{360}{30}\)
⇒ x = 12
First angle of quadrilateral is 3x = 3 × 12 = 36°
Second angle of quadrilateral is 5x = 5 × 12 = 60°
Third angle of quadrilateral is 9x = 9 × 12 = 108°
Fourth angle of quadrilateral is 13x = 13 × 12 = 156°
![]()
Question 2.
If the diagonals of a parallelogram are equal, then show that it is a rectangle.
Solution:
Given: ABCD is a parallelogram, in which diagonal AC and BD are equal.
To prove that: ABCD is a rectangle.
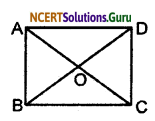
Proof: In ∆ABC and ∆DCB.
AC = BD (Given)
BC = GB (Common)
AB = DC (Opposite sides of a parallelogram)
Therefore, by S-S-S congruency condition
∆ABC ≅ ∆DCB
So, ∠ABC = ∠BCD (By C.P.C.T)
But, ∠ABC + ∠BCD = 180 (Sum of interior angles of the same side of transversal)
⇒ 2∠ABC = 180 (∵ ∠ABC = ∠BCD)
⇒ ∠ABC = 90°
Therefore, paraileiogram ABCD is a rectangle.
![]()
Question 3.
Show that if the diagonals of a quadrilateral bisect each other at right angles, then it is a rhombus.
Solution:
Given: ABCD is a quadrilateral, in which diagonal AC and BD intersect each other at a right angle.
To prove that ABCD is a Rhombus.
Proof: In ∆AOD and ∆AOB,
AO = OA (Common)
OD = OB (Given)
∠AOD = ∠AOB (each 90°)
By S-A-S congruency condition
∠AOU ≅ ∠AQB
So, AD = AB …..(i) (By C.P.C.T)
Similarly, AD = BC ……(ii)
and AB = CD ……(iii)
By equation (i), (ii) and (iii)
AB = BC = CD = DA
Therefore, ABCD is a rhombus.
![]()
Question 4.
Show that the diagonals of a square are equal and bisect each other at right angles.
Solution:
Given: ABCD is a square, in which diagonal AC and BD intersect each other at Q.
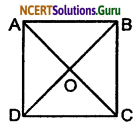
To prove that:
(i) AC = BD
(ii) Diagonal bisects each other at right angle.
Proof:
(i) In ∆ABC and ∆BAD
AB = BA (Common)
BC = AD (sides of square)
∠ABC = ∠BAD (each 90°)
By S-A-S congruency condition
∆ABC ≅ ∆BAD
AC = BD (By C.P.C.T.)
(ii) In ∆AOB and ∆COD,
AB = CD (Sides of square)
∠AOB = ∠COD (Vertically opposite angles)
∠OBA = ∠OCD (Alternate interior angle)
Therefore, by A-S-A congruency condition
∆AOB ≅ ∆COD
So, OA = OC (By C.P.C.T.)
and OB = OD (By C.P.C.T)
Now, In ∆AOD and ∆COD
AD = CD (Sides of square)
OA = OC (Prove above)
OD = OD (Common)
By S-S-S ccngruency condition
∆AOD = ∆COD
So, ∠AOD = ∠COD (By C.P.C.T)
But, ∠AOD + ∠COD = 180 (Linear pair)
⇒ ∠AOD + ∠AOD = 180 (∵ ∠AOD = ∠COD)
⇒ 2∠AOD = 180
⇒ ∠AOD = 90° …..(ii)
Therefore, from equations (i) and (ii) it is dear that diagonal of a square bisect each other at a right angle.
![]()
Question 5.
Show that if the diagonals of a quadrilateral are equal and bisect each other at right angles, then it is a square.
Solution:
Given: ABCD is a quadrilateral in which diagonal AC and BD bisect each other at right angles.
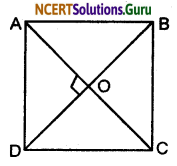
To prove that: ABCD is a square.
Proof: In ∆AOB and ∆COD
AO = CO (Given)
∠AOB = ∠COD (Vertically opposite angles)
OB = OD (Given)
By S-A-S Congruency Condition.
∆AOB ≅ ∆COD
So, AB = CD …..(i) (By C.P.C.T)
and ∠OAB = ∠OCD (By C.P.C.T)
But it is the pair of alternate interior angles and we know that if pair of alternate interior angles are equal then the two lines are parallel.
∴ AB || CD …..(ii)
From (i) and (ii)
ABCD is a parallelogram
Now, in ∆AOD and ∆COD
AO = OC (Given)
∠AOD = ∠COD (Each 90°)
OD = OD (Common)
By S-A-S congruency condition
∆AOD ≅ ∆COD
AD = CD …..(iii) (ByC.P.C.T.)
Again, AD = BC ……(iv)
(Opposite sides of parallel gram ABCD)
From equation (i), (iii) and (iv)
Therefore ABCD is a square.
![]()
Question 6.
Diagonal AC of a parallelogram ABCD bisects ∠A [see Fig. 8.19]. Show that
(i) it bisects ∠C also.
(ii) ABCD is a rhombus.
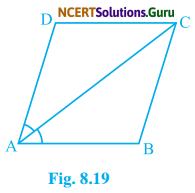
Solution:
(i) In ∆DAC and ∆BCA
DA = BC (Opposite sides of parallelogram)
DC = BA (Opposite sides of parallelogram)
AC = CA (Common)
By S-S-S congruency condition
∆DAC = ∆BCA
So, ∠DAC = ∠BCA …..(i) (By C.P.C.T)
and ∠ACD = ∠BAC ……(ii) (By C.P.C.T)
Add equation (i) and (ii)
∠DAC + ∠ACD = ∠BCA + ∠BAC
∠DAC + ∠ACD = ∠BCA + ∠DAC (∵ ∠DAC = ∠BAC given)
Therefore, ∠ACD = ∠BCA
or, AC bisect ∠C.
(ii) We have,
∠ACD = ∠BAC …..(iii) (From equation (ii))
But ∠BAC = ∠CAD …..(iv)
From (iii) and (iv)
∠ACD = ∠CAD
∴ DA = DC
(Side opposite to equal angles are equal)
But DA = BC (Opposite side of || gm)
∴ AB = BC = CD = DA
Therefore, ABCD is a rhombus.
![]()
Question 7.
ABCD is a rhombus. Show that diagonal AC bisects ∠A as well as ∠C and diagonal BD bisects ∠B as well as ∠D.
Solution:
In this Fig. ABCD is a rhombus.
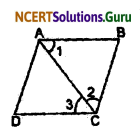
Therefore, AB = BC = CD = AD
In ∆ABC,
AB = BC (Because ABCD is a rhombus)
∴ ∠1 = ∠2 (Angle opposite to equal sides are equal)
But, ∠1 = ∠3 …….(ii) (Alternate interior angles)
From (i) and (ii)
∠1 = ∠3
∴ AC bisects ∠C.
Similarly, we can prove AC bisects ∠A, and BD bisects both ∠B as well as ∠D.
Question 8.
ABCD is a rectangle in which diagonal AC bisects. ∠A as well as ∠C. Show that
(i) ABCD is a square.
(ii) diagonal BD bisects ∠B as well as ∠D.
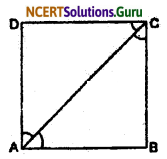
Solution:
(i) We have given ABCD is a rectangle.
∠A = ∠C (each 90°)
or, \(\frac {1}{2}\) ∠A = \(\frac {1}{2}\) ∠C
∠DAC = ∠DCA (AC bisects ∠A as well as ∠C)
So, AD = CD ……(i) (Sides opposite to equal angles are equal)
But, AD = BC ……(ii) (Opposite sides of rectangle)
From equation (i) and (ii)
AB = BC = CD = AD
∴ ABCD is rhombus.
But, each angle of rhombus ABCD is 90°.
Therefore, ABCD is a square.
(ii) We know that diagonals of squares bisect opposite angles.
Therefore, diagonal BD bisects both ∠B and ∠D.
![]()
Question 9.
In parallelogram ABCD, two points P and Q are taken on diagonal BD such that DP = BQ (see Fig 8.20) Show that:
(i) ∆APD ≅ ∆CQB
(ii) AP = CQ
(iii) ∆AQB = ∆CPD
(iv) AQ = CP
(v) APCQ is a parallelogram.
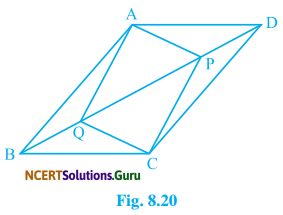
Solution:
Given: ABCD is a parallelogram, and two points P and Q are taken on diagonal BD such that DP = BQ.
To prove that:
(i) ∆APD ≅ ∆CQB
(ii) AP = CQ
(iii) ∆AQB = ∆CPD
(iv) AQ = CP
(v) APCQ is a parallelogram.
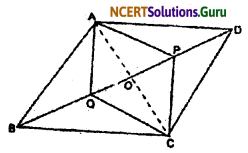
Construction: Draw diagonal AC of parallelogram ABCD intersecting BD at O.
Proof:
(i) In ∆APD and ∆CQB
∠ADP = ∠CBQ (Pair of alternate interior angles)
AD = BC (Opposite sides of || gm ABCD)
PD = QB (Given)
By S-A-S congruency condition.
∠APD ≅ ∠CQB
(ii) We have
∠APD ≅ ∠CQB (Prove above)
∴ AP = CQ (By C.P.C.T.)
(iii) In ∆AQB and ∆CPD
∠LBQ = ∠CDP (Pair of alternate interior angles)
AB = CD (Opposite sides of parallelogram ABCD)
BQ = DP (Given)
By S-A-S congruency condition
∆AQB ≅ ∆CPD
(iv) We have
∆AQB ≅ ∆CPD (Prove above)
∴ AQ = CP (By C.P.C.T)
(v) In ∆QCP,
AQ = CP (Prove above from (iv))
and AP = CQ (Prove above from (ii))
We know that if both opposite pairs are equal then the parallelogram.
Hence, APCQ is a parallelogram.
![]()
Question 10.
ABCD is a parallelogram and AP and CQ are perpendiculars from vertices A arid C on diagonal BD respectively (see fig 8.21). Show that
(i) ∆APB ≅ ∆CQD
(ii) AP = CQ
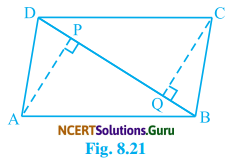
Solution:
(i) In ∆APB and ∆CQD
∠APB = ∠CQD (Each 90°)
AB = CD (Opposite sides of || gm ABCD)
and, ∠ABP = ∠CDQ (Alternate interior angles)
By A-S-A Congruency condition
∆APB = ∆CQD
(ii) We have
∆APB = ∆CQD (Prove above)
∴ AP = CQ (By C.P.C.T)
Question 11.
In ∆ABC and ∆DEF, AB = DE and AB || DE, BC = EF and BC || EF. Vertices A, B, and C are joined to vertices D, E and F respectively (see fig 8.22). Show that
(i) quadrilateral ABED is a parallelogram.
(ii) quadrilateral BEFC is a parallelogram.
(iii) AD || CF and AD = CF
(iv) quadrilateral ACFD is a parallelogram
(v) AC = DF
(vi) ∆ABC ≅ ∆DEF
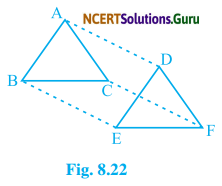
Solution:
Given: AB = DE and AB || DE,
BC = EF and BC || EF
To prove that:
(i) quadrilateral ABED is a parallelogram.
(ii) quadrilateral BEFC is a parallelogram.
(iii) AD || CF and AD = CF
(iv) quadrilateral ACFD is a parallelogram
(v) AC = DF
(vi) ∆ABC ≅ ∆DEF
Proof:
(i) We have
AB = DE and AB || DE
We know that if one opposite pair of a quadrilateral are parallel and equal, then the quadrilateral is a parallelogram.
∴ Quadrilateral ABDE is a parallelogram.
(ii) We have
BC = EF and BC || EF
Therefore, quadrilateral BCEF is a parallelogram.
(iii) From (i) we have
ABED is a parallelogram.
AD = BE and AD || BE …….(A)
(Opposite sides of parallelogram ABED)
Again, From (ii)
BEFC is a parallelogram,
BE = CF and BE || CF ……..(B)
(Opposite sides of parallelogram BEFC)
From equation (A) and (B)
AD || CF and AD = CF
![]()
(iv) We have
AD || CF and AD = CF (Prove above from part (iii))
We know that, if one opposite pair of a quadrilateral are parallel and equal, then the quadrilateral is a parallelogram.
∴ ACFD is a parallelogram.
(v) We have,
ACFD is a parallelogram
(Prove above from part IV)
∴ AC || DF
(Opposite sides of parallelogram ACFD)
and AC = DF
(vi) In ∆ABC and ∆DEF
AB = DE (Given)
BC = EF (Given)
AC = DF (Prove above)
By S-S-S Congruency condition,
∆ABC ≅ ∆DEF.
![]()
Question 12.
ABCD is, a trapezium in which AB || CD and AD = BC (see fig 8.23). Show that
(i) ∠A = ∠B
(ii) ∠C = ∠D
(iii) ∆ABC ≅ ∆BAD
(iv) Diagonal AC = Diagonal BD.
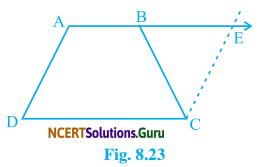
Solution:
Given: ABCD is a trapezium in which AB || CD and AD = BC.
To prove that:
(i) ∠A = ∠B
(ii) ∠C = ∠D
(iii) ∆ABC ≅ ∆BAD
(iv) Diagonal AC = diagonal BD.
Construction: Through C draw CE || AD which intersect AB produced at E, and join ACBD.
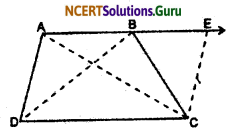
Proof: (i) We have,
AB || CD (Given)
AD || CE (By construction)
Therefore, AECD is a parallelogram.
So, AD = CE …..(i)
(Opposite sides of || gm)
But AD = BC ……(ii) (Given)
From (i) and (ii)
BC = CE
∴ ∠CBE = ∠CEB
(Angle opposite to equal sides are equal)
Now, ∠A + ∠CEB = 180°
(Sum of interior angles of the same side of transversal)
or, ∠A + ∠CBE = 180° ……(iii) (∵ ∠CEB = ∠CBE)
But, ∠B + ∠CBE = 180° ……(iv) (Linear pair)
From equation (iii) and (iv)
or, ∠A = ∠B
(ii) We have AB || CD
∴ ∠A + ∠D = 180° …..(v)
(Sum of an interior angle of the same side of transversal)
and, ∠C + ∠B = 180° ……(vi)
(Sum of interior angle of the same side of transversal)
From equation (v) and (vi)
∠A + ∠D = ∠C + ∠B
But, ∠A = ∠B (Prove above)
∴ ∠C = ∠D
![]()
(iii) In ∆ABC and ∆BAD
AB = BA (Common)
BC = AD (Given)
∠B = ∠A (Prove above)
By S-A-S congruency condition
∆ABC ≅ ∆BAD
(iv) We have
∆ABC ≅ ∆BAD (Prove above)
∴ AC = BD (By CPCT)
Therefore, diagonal AC = diagonal BD.