These NCERT Solutions for Class 6 Maths Chapter 14 Practical Geometry Ex 14.5 Questions and Answers are prepared by our highly skilled subject experts.
NCERT Solutions for Class 6 Maths Chapter 14 Practical Geometry Exercise 14.5
Question 1.
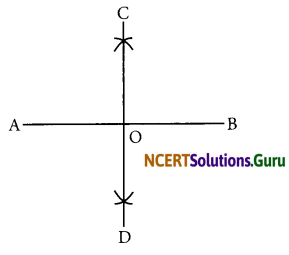
Draw \(\overline{\mathrm{AB}}\) of length 7.3 cm and find its axis of symmetry.
Answer:
Axis of symmetry of line segment \(\overline{\mathrm{AB}}\) will be the perpendicular bisector of \(\overline{\mathrm{AB}}\). So, draw the perpendicular bisector of \(\overline{\mathrm{AB}}\).
Steps of construction:
- Draw a line segment \(\overline{\mathrm{AB}}\) = 7.3 cm
- Taking A and B as centres and radius more than half of AB, draw two arcs which intersect each other at C and D.
- Join CD. Then CD is the axis of symmetry of the line segment AB.
![]()
Question 2.
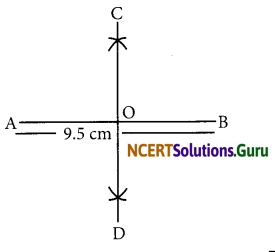
Draw a line segment of length 9.5 cm and construct its perpendicular bisector.
Answer:
Steps of construction:
- Draw a line segment \(\overline{\mathrm{AB}}\) = 9.5 cm
- Taking A and B as centres and radius more than half of AB, draw two arcs which intersect each other at C and D.
- Join CD. Then CD is the perpendicular bisector of \(\overline{\mathrm{AB}}\) .
Question 3.
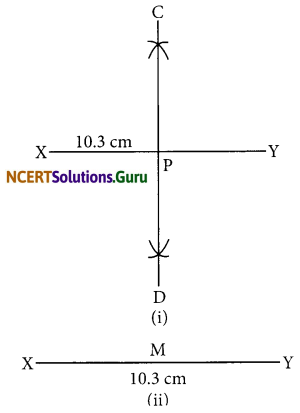
Draw the perpendicular bisector of \(\overline{\mathrm{XY}}\) whose length is 10.3 cm.
(a) Take any point P on the bisector drawn.
Examine whether PX = PY.
(b) If M is the mid-point of \(\overline{\mathrm{XY}}\) , what can you say about the lengths MX and XY?
Answer:
Steps of construction:
- Draw a line segment \(\overline{\mathrm{XY}}\) = 10.3 cm
- Taking X and Y as centres and radius more than half of AB, draw two arcs which intersect each other at C and D.
- Join CD. Then CD is the required perpendicular bisector of \(\overline{\mathrm{XY}}\) .
Now:
(a) Take any point P on the bisector drawn. With the help of divider we can check that \(\overline{\mathrm{PX}}\) = \(\overline{\mathrm{PY}}\)
(b) If M is the mid-point of \(\overline{\mathrm{PX}}\) and \(\overline{\mathrm{MX}}\) – 1/2\(\overline{\mathrm{XY}}\)
![]()
Question 4.
Draw a line segment of length 12.8 cm. Using compasses, divide it into four equal parts. Verify by actual measurement.
Answer:
Steps of construction:
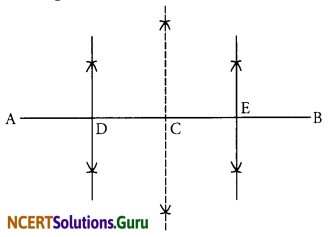
- Draw a line segment AB = 12.8 cm
- Draw the perpendicular bisector of \(\overline{\mathrm{AB}}\) which cuts it at C. Thus, C is the midpoint of \(\overline{\mathrm{AB}}\).
- Draw the perpendicular bisector of \(\overline{\mathrm{AC}}\) which cuts it at D. Thus D is the midpoint of.
- Again, draw the perpendicular bisector of \(\overline{\mathrm{CB}}\) which cuts it at E. Thus, E is the mid-point of \(\overline{\mathrm{CB}}\).
- Now, point C, D and E divide the line segment \(\overline{\mathrm{AB}}\) in the four equal parts.
- By actual measurement, we find that \(\overline{\mathrm{AD}}=\overline{\mathrm{DC}}=\overline{\mathrm{CE}}=\overline{\mathrm{EB}}\) = 3.2 cm
Question 5.
With \(\overline{\mathrm{PQ}}\) of length 6.1 cm as diameter,
draw a circle.
Answer:
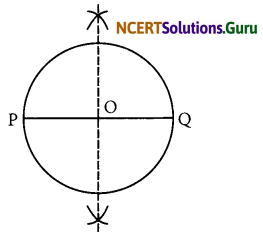
Steps of construction:
- Draw a line segment \(\overline{\mathrm{PQ}}\) = 6.1 cm.
- Draw the perpendicular bisector of PQ which cuts, it at O. Thus O is the mid-point of \(\overline{\mathrm{PQ}}\).
- Taking O as centre and OP or OQ as radius draw a circle where diameter is the line segment \(\overline{\mathrm{PQ}}\).
![]()
Question 6.
Draw a circle with centre C and radius 3.4 cm. Draw any chord \(\overline{\mathrm{AB}}\). Construct the perpendicular bisector \(\overline{\mathrm{AB}}\) and examine if it passes through C.
Answer:
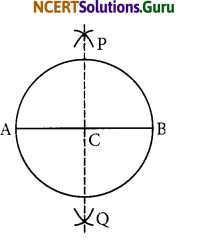
Steps of construction:
- Draw a circle with centre C and radius 3.4 cm.
- Draw any chord \(\overline{\mathrm{AB}}\).
- Taking A and B as centres and radius more than half of \(\overline{\mathrm{AB}}\), draw two arcs which cut each other at P and Q.
- Join PQ. Then PQ is the perpendicular bisector of \(\overline{\mathrm{AB}}\).
- This perpendicular bisector of \(\overline{\mathrm{AB}}\) passes through the centre C of the circle.
Question 7.
Repeat Q6, if \(\overline{\mathrm{AB}}\) happens to be a diameter.
Answer:
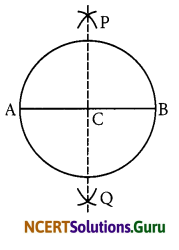
Steps of construction:
- Draw a circle with centre C and radius 3.4 cm.
- Draw its diameter \(\overline{\mathrm{AB}}\).
- Taking A and B as centres and radius more than half of it, draw two arcs which intersect each other at P and Q.
- Join PQ. Then PQ is the perpendicular bisector of \(\overline{\mathrm{AB}}\) .
- We observe that this perpendicular bisector of \(\overline{\mathrm{AB}}\) passes through the centre C of the circle.
![]()
Question 8.
Draw a circle of radius 4 cm. Draw any two of its chords. Construct the perpendicular bisectors of these chords.
Where do they meet?
Answer:
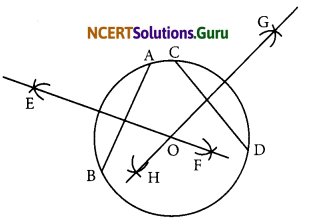
Steps of construction:
- Draw the circle with O and radius 4 cm.
- Draw any two chords \(\overline{\mathrm{AB}}\) and \(\overline{\mathrm{CD}}\) in this circle.
- Taking A and B as centres and radius more than half AB, draw two arcs which intersect each other at E and F.
- Join EF. Thus EF is the perpendicular bisector of chord \(\overline{\mathrm{CD}}\).
- Similarly draw GH the perpendicular bisector of chord \(\overline{\mathrm{CD}}\).
- These two perpendicular bisectors meet at O, the centre of the circle.
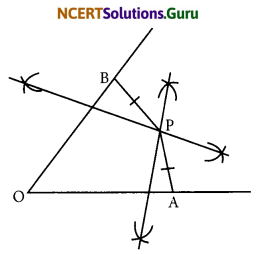
Question 9.
Draw any angle with vertex O. Take a point A on one of its arms and B on another such that OA = OB. Draw the perpendicular bisectors of \(\overline{\mathrm{OA}}\) and \(\overline{\mathrm{OB}}\). Let them meet at P. Is PA = PB?
Answer:
Steps of construction:
- Draw any angle with vertex O.
- Take a point A on one of its arms and B on another such that OA = OB.
- Draw perpendicular bisector of \(\overline{\mathrm{OA}}\) and OB.
- Let them meet at P. Join PA and PB.
- With the help of divider, we check that \(\overline{\mathrm{PA}}=\mathrm{PB}\)