These NCERT Solutions for Class 10 Maths Chapter 11 Constructions Ex 11.1 Questions and Answers are prepared by our highly skilled subject experts.
NCERT Solutions for Class 10 Maths Chapter 11 Constructions Exercise 11.1
![]()
Question 1.
Draw a line segment of length 7.6 cm and divide it in the ratio 5:8. Measure the two parts.
Solution:
Steps of Construction:
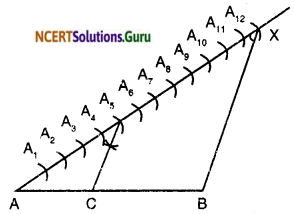
- Draw a line segment AB = 7.6 cm.
- Draw an acute angle BAX on base AB. Mark the ray as AX.
- Locate 13 points A1, A2, A3, …… , A13 on the ray AX so that AA1 = A1A2 = ……… = A12A13
- Join A13 with B and at A5 draw a line ∥ to BA13, i.e. A5C. The line intersects AB at C.
On measure AC = 2.9 cm and BC = 4.7 cm.
Then AC : CB = 5 : 8
Since A3C is parallel to A13B therefore
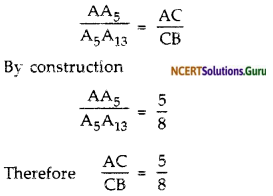
This show that C divides AB in the ratio 5
![]()
Question 2.
Construct a triangle of sides 4 cm, 5 cm and 6 cm and then a triangle similar to it whose sides are \(\frac { 2 }{ 3 }\) of the corresponding sides of the first triangle.
Solution:
Steps of Construction:
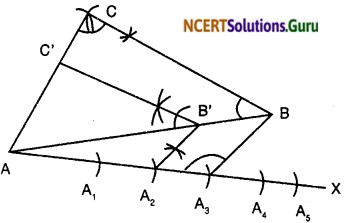
First we draw line AB 6 cm and then cut an arc AC = 4 cm. After that cut an another are BC = 5 cm. Join A to C and B to C. We find a AABC.
- Draw ray AX making an acute angle with AB.
- Locate points A1, A2, A3, A4, A5 on AX so that AA1 = A1A3, = A2A3
- Join BA3.
- Join A2B’ such that A2B’ || A3B and (∠AA3B = ∠AA2B’)
- Through B draw a ray B’C || BC’ and ∠ABC – ∠AB’C.
Hence ABC is the required triangle.
![]()
Question 3.
Construct a triangle with sides 5 cm, 6 cm and 7 cm and then another triangle whose sides are \(\frac { 7 }{ 5 }\) of the corresponding sides of the first triangle.
Solution:
Steps of Construction:
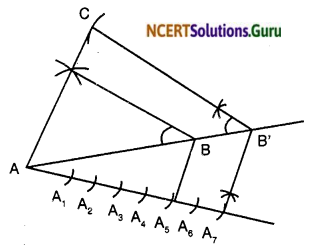
- Draw a ΔABC with AB = 5 cm, BC = 7 cm and AC = 6 cm.
- Draw an acute angle CBA below BC at point B.
- Mark the ray BX as B1, B2, B3, B4, B5, B6 and B7 such that BB1= B1B2 = B2B3 = B3B4 = B4B5 = B5B6 = B6B7.
- Join B5 to C.
- Draw B7C’ parallel to B5C, where C’ is a point on extended line BC.
- Draw A’C’ ∥ AC, where A’ is a point on extended line BA.
∴ A’BC’ is the required triangle.
Question 4.
Construct an isosceles triangle whose base is 8 cm and altitude 4 cm and then another triangle whose sides are 1\(\frac { 1 }{ 2 }\) times the corresponding sides of the isosceles triangle.
Solution:
Steps of Construction:
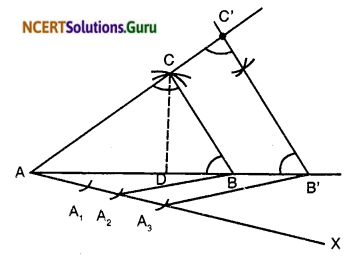
- Draw base AB = 8 cm.
- Draw perpendicular bisector of AB. Mark CD = 4 cm, on ⊥ bisector where D is mid-point on AB.
- Draw an acute angle BAX, below AB at point A.
- Mark the ray AX with A1, A2, A3 such that AA1 =A1A2 = A2A3
- Join A2 to B. Draw A3B’ ∥ A2 B, where B’ is a point on extended line AB.
- At B’, draw B’C’ 11 BC, where C’ is a point on extended line AC.
∴ ∆AB’C’ is the required triangle.
![]()
Question 5.
Draw a triangle ABC with side BC = 6 cm, AB = 5 cm and ∠ABC = 60°. Then construct a triangle whose sides are \(\frac { 3 }{ 4 }\) of the corresponding sides of the triangle ABC.
Solution:
Steps of Construction:
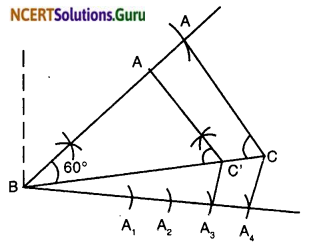
- Draw a line segment BC = 6 cm and at point B draw an ∠ABC = 60°.
- Cut AB = 5 cm. Join AC. We obtain a ΔABC.
- Draw a ray BX making an acute angle with BC on the side opposite to the vertex A.
- Locate 4 points A1, A2, A3 and A4 on the ray BX so that BA1 = A1A2 = A2A3 = A3A4.
- Join A4 to C.
- At A3, draw A3C’ ∥ A4C, where C’ is a point on the line segment BC.
- At C’, draw C’A’ ∥ CA, where A’ is a point on the line segment BA.
∴ ∆A’BC’ is the required triangle.
![]()
Question 6.
Draw a triangle ABC with side BC = 7 cm, ∠B = 45°, ∠A = 105°. Then, construct a triangle whose sides are \(\frac { 4 }{ 3 }\) times the corresponding sides of ∆ABC.
Solution:
In ∆ABC, ∠A + ∠B + ∠C = 180°
⇒ 105° + 45° + ∠C = 180°
⇒ 150° + ∠C = 180°
⇒ ∠C = 30°
Steps of Construction:
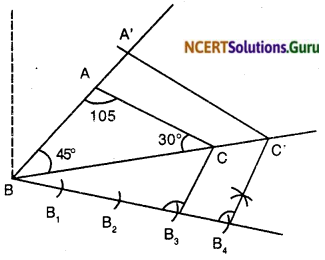
- Draw a line segment BC = 7 cm. At point B, draw an ∠B = 45° and at point C, draw an ∠C = 30° and get ΔABC.
- Draw an acute ∠CBX on the base BC at point B. Mark the ray BX with B1, B2, B3, B4, such that BB1 = B1B2 = B2B3 = B3B4
- Join B3 to C.
- Draw B4C’ ∥ B3C, where C’ is point on extended line segment BC.
- At C’, draw C’A’ ∥ AC, where A’ is a point on extended line segment BA.
∴ ∆A’BC’ is the required triangle.
![]()
Question 7.
Draw a right triangle in which the sides (other than hypotenuse) are of lengths 4 cm and 3 cm. Then construct another triangle whose sides are \(\frac { 5 }{ 3F }\) times the corresponding sides of the given triangle.
Solution:
Steps of Construction:
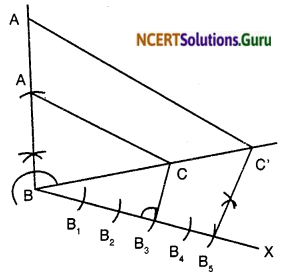
- Draw a right angled ∆ABC with AB = 4 cm, AC = 3 cm and ∠A = 90°.
- Make an acute angle BAX on the base AB at point A.
- Mark the ray AX with A1, A2, A3, A4, A5 such that AA1 = A1A2 = A2A3 = A3A4 = A4A5.
- Join A3B. At A5, draw A5B’ ∥ A3B, where B’ is a point on extended line segment AB.
- At B’, draw B’C’ ∥ BC, where C’ is a point on extended line segment AC.
∴ ∆AB’C’ is the required triangle.