These NCERT Solutions for Class 10 Maths Chapter 10 Circles Ex 10.2 Questions and Answers are prepared by our highly skilled subject experts.
NCERT Solutions for Class 10 Maths Chapter 10 Circles Exercise 10.2
![]()
Question 1.
From a point Q, the length of the tangent to a circle is 24 cm and the distance of Q from the centre is 25 cm. The radius of the circle is
(a) 7 cm Sol.
(b) 12 cm
(c) 15 cm
(d) 24.5 cm
Solution:

Therefore, radius of the circle is 7 cm
So, option (A) of the give question is right.
Question 2.
In figure, if TP and TQ are the two tangents to a circle with centre O so that ∠POQ = 110°, then ∠PTQ is equal to
(a) 60°
(b) 70°
(c) 80°
(d) 90°
Solution:
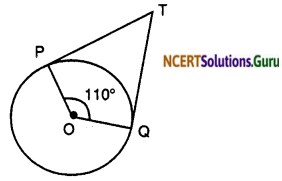
∠OPT = 90°
∠OQT = 90°
∠POQ = 110°
TPOQ is a quadrilateral,
∴ ∠PTQ + ∠POQ = 180° ⇒ ∠PTQ + 110° = 180°
⇒ ∠PTQ = 180°- 110° = 70°
Hence, correct option is (b).
![]()
Question 3.
If tangents PA and PB from a point P to a circle with centre O are inclined to each other at angle of 80°, then ∠POA is equal to
(a) 50°
(b) 60°
(c) 70°
(d) 80°
Solution:
In AOAP and AOBP
OA = OB [Radii]
PA = PB
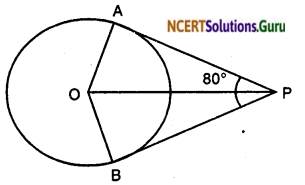
[Lengths of tangents from an external point are equal]
OP = OP [Common]
∴ ∆OAP ≅ ∆OBP [SSS congruence rule]
∠AOB + ∠APB = 180° ⇒ ∠AOB + 80° = 180°
⇒ ∠AOB = 180° – 80° = 100°
From eqn. (i), we get
⇒ ∠POA = \(\frac { 1 }{ 2 }\) x 100° = 50°
Hence, correct option is (a)
Question 4.
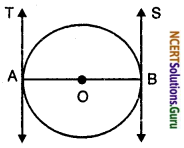
Prove that the tangents drawn at the ends of a diameter of a circle are parallel.
Solution:
AB is a diameter of the circle, p and q are two tangents.
OA ⊥ p and OB ⊥ q
∠1 = ∠2 = 90°
⇒ p || q ∠1 and ∠2 are alternate angles]
Question 5.
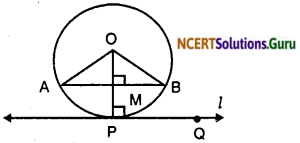
Prove that the perpendicular at the point of contact to the tangent to a circle passes through the centre.
Solution:
XY tangent to the circle C(0, r) at B and AB ⊥ XY. Join OB.
∠ABY = 90° [Given]
∠OBY = 90°
[Radius through point of contact is perpendicular to the tangent]
∴ ∠ABY + ∠OBY = 180° ⇒ AB Oiscollinear
∴ AB passes through centre of the circle.
![]()
Question 6.
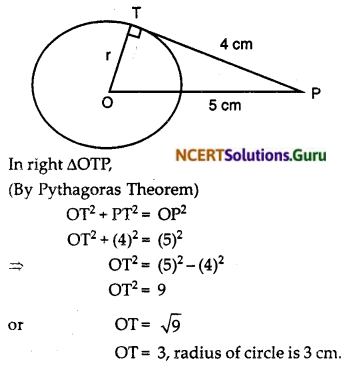
The length of a tangent from a point A at distance 5 cm from the centre of the circle is 4 cm. Find the radius of the circle.
Solution:
OA = 5 cm, AP = 4 cm OP = Radius of the circle
∠OPA = 90° [Radius and tangent are perpendicular]
Question 7.
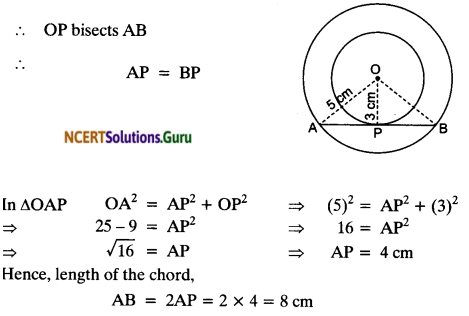
Two concentric circles are of radii 5 cm and 3 cm. Find the length of the chord of the larger circle which touches the smaller circle.
Solution:
Radius of larger circle = 5 cm Radius of smaller circle = 3 cm
OP ⊥ AB
[Radius of circle is perpendicular to the tangent]
AB is a chord of the larger circle
![]()
Question 8.
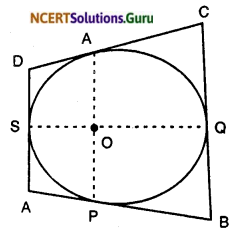
A quadrilateral ABCD is drawn to circumscribe a circle (see figure). Prove that AB + CD = AD + BC.
Solution:
AP = AS … (i)
[Lengths of tangents from an external point are equal]
BP = BQ … (ii)
CR = CQ … (iii)
DR = DS … (iv)
Adding equations (i), (ii), (iii) and (iv), we get
AP + BP + CR + DR = AS + BQ + CQ + DS
⇒ (AP + BP) + (CR + DR) = (AS + DS) + (BQ + CQ)
⇒ AB + CD = AD + BC
Hence proved.
Question 9.
In figure, XY and X’Y’ are two parallel tangents to a circle , x with centre O and another tangent AB with point of contact C intersecting XY at A and X’Y’ at B. Prove that ∠AOB = 90°.
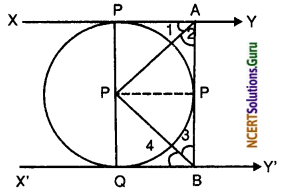
Solution:
To Prove : ∠AOC = 90°
Join OC
XY and X’Y’ are two tangents
XY || X’Y’ (given) and AB is transversal … (i)
∠PAC + ∠QBC = 180° (Sum of int ∠s)
In ∆PAO and ∆CAO, we have
PA = AC (Tangent drawn from exterior point)
AO = AO (common)
PO = QC (radii of same circle)
∆ ∆PAO ≅ ∆CDO
⇒ ∠1 = ∠2
Similarly ∠3 = ∠4
Now, ∠PAC + ∠QBC = 180°
⇒ ∠1 + ∠2 + ∠3 + ∠4 = 180°
[∵ ∠1 = ∠2 and ∠4 = ∠3]
⇒ 2(∠2 + ∠3) = 180°
or ∠2 + ∠3 = 90°
Now, In ∆ OAB,
∠AOB + ∠2 + ∠3= 180° [put ∠2 + ∠3 = 90°]
or ∠AOB+ 90°= 180°
⇒ ∠AOB = 90°
![]()
Question 10.
Prove that the angle between the two tangents drawn from an external point to a circle is supplementary to the angle subtended by the line segment joining the points of contact at the centre.
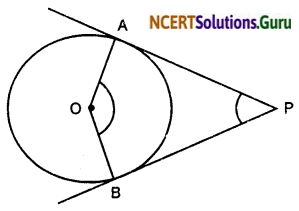
Solution:
Given : Two tangents PA and PB are drawn from the point P to the circle with centre O. A and B are the points of contact of two tangents PA and PB respectively.
To Prove : ∠APB + ∠AOB = 180°
Construction: Join OA and OB
Proof : Since the tangent PA is drawn to the circle at A with centre O, we have;
OA ⊥ PA ⇒ ∠OAP = 90°
Similarly, since the tangent PB is drawn to the circle at B with centre O. we have,
OB ⊥ PB ⇒ OBP = 90°
We know the sum of four angles of a quadrilateral is 360°
Sc, in the quadrilateral, OA PB, we have
∠OAP + ∠APB + ∠OBP + ∠AOB = 360°
⇒ ∠APB + ∠AOB = 360° (∠OAP + ∠OBP) = 360° – 180°
⇒ ∠APB + ∠AOB = 180° Hence Proved.
Question 11.
Prove that the parallelogram circumscribing a circle is a rhombus.
Solution:
Given: ABCD is a || gm AB, BC, CD and DA are touching a circle.
To Prove: AB = BC = CD = DA
Proof : Since the length of two tangents drawn from an external point to a circle are equal, we have
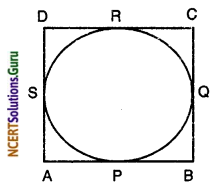
AP = AS, BP = BQ, CR = CQ and DR = DS
AB + CD = AP + BP + CR + DR
AD + BC = AS + BQ + CQ + DS
= AS + DS + BQ + CQ
= AD + BC
⇒ AB + CD = AD + BC
⇒ 2AB = 2AD
w AB = AD
But AB= CD and BC = AD
AB = BC = CD = DA
Hence || gm ABCD is a rhombus.
![]()
Question 12.
A triangle ABC is drawn to circumscribe a circle of radius 4 cm such that the segments BD and DC into which BC is divided by the point of contact D are of lengths 8 cm and 6 cm respectively (see figure). Find the sides AB and AC.
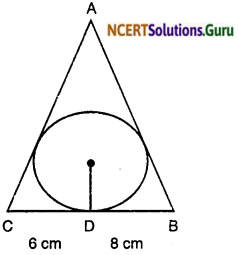
Solution:
Let the sides AB, BC and AC touch the in circle at E, D and F respectievly. Join the centre O of the circle with A, B, C, D, E and F.
The point D divide BC in two parts CD = 6 cm and BD = 8 cm
Since tangent to a circle from an external point are equal CD = CF = 6 cm and DB = BE = 8 cm.
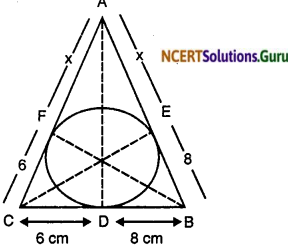
AF = AE = x cm (say)
OD= OE = OF = 4 [radii of the incircle]
Now, Area of ∆AOC = \(\frac { 1 }{ 2 }\) (6 + x) x 4
= (6 + x) × 2 = (12 + 2x) sq. cm. … (i)
Similarly Area of ∆AOB = \(\frac { 1 }{ 2 }\) (8 + x) × 4
= (16 + 2x) sq. cm … (ii)
Area of ABOC = \(\frac { 1 }{ 2 }\) (6 + 8) x 4 = 28 sq. cm … (iii)
Adding equations (i), (ii) and (iii), we have
Area of ∆ABC = [(12 + 2x) + (16 + 2x) + 28] sq.
= [56 + 4x] sq. cm … (iv)
Again perimeter of ∆ABC = AB + BC + CA = (x + 8) + (6 + 8) + (6 + x)
= (28 + 2x) cm
 AB = x + 8 = 7 + 8 = 15 cm
AB = x + 8 = 7 + 8 = 15 cm
AC = x + 6 = 7 + 6 = 13 cm.
![]()
Question 13.
Prove that opposite sides of a quadrilateral circumscribing a circle subtend supplementary angles at the centre of the circle.
Solution:
Given : A circle with centre O touches the side, PQ, QR, RS and PS of quadrilateral at the points A, B, C and D respectively.
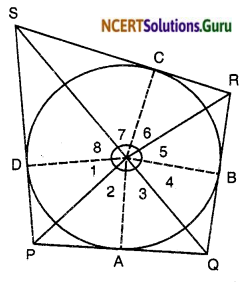
To Prove : ∠PQQ + ∠ROS = 180°
and ∠POS + ∠QOR = 180°
Construction: Join OA, OB, OC and OD.
Proof: In ∆POD and ∆POA .
PA = FD [tangents from expemal point]
OP = OP [common]
∠ODP = ∠ODA [each 90°]
∆POD = ∆POA [RHS congruency]
∠1 = ∠2 [C.P.C.T]
Similarly we have
∠3= ∠4; ∠5 = ∠6 and ∠7 = ∠8
Now ∠1 + ∠2 + ∠3+ ∠4 + ∠5 +
∠6 + ∠7 + ∠8 = 360°
Using the above result
∠2 + ∠2 + ∠3+ ∠3+ ∠6 + ∠6 + ∠7 + ∠7 = 360°
or 2(∠2 + ∠3)+ (∠6 + ∠7)
\(\frac{360^{\circ}}{2}\) = 180°
and
∠1 + ∠1 + ∠4 + ∠4 + ∠5 + ∠5 + ∠8 + ∠8 = 360°
or 2(∠1 + ∠4 + ∠5 + ∠8) = 360°
or ∠1 + ∠4 + ∠5 + ∠8 = \(\frac{360^{\circ}}{2}\)
or (∠1 + ∠8) + (∠4 + ∠5) = 180°
or ∠POS +∠QOR = 180°