If you’re looking for a way to enhance your Class 9 Maths, then look no further than the NCERT MCQ Questions for Class 9 Maths Chapter 9 Areas of Parallelograms and Triangles with Answers. MCQ Questions for Class 9 Maths with Answers is perfect for those who are in Class 9 Maths and want to get ahead of everyone else by mastering the subject skills as soon as possible! Go ahead and find Class 9 Maths Chapter 9 Areas of Parallelograms and Triangles Objective Questions.
Areas of Parallelograms and Triangles Class 9 MCQs Questions with Answers
Solving MCQ on Areas of Parallelograms and Triangles Multiple Choice Questions of Class 9 Maths with Answers can be of great help to students as they will be aware of all the concepts. These Class 9 Maths Chapter 9 MCQ with Answers pave for a quick revision, thereby helping you learn more about this subject.
Question 1.
What is the area of a parallelogram?
(a) \(\frac { 1 }{ 2 }\) × Base × Altitude
(b) Base × Altitude
(c) \(\frac { 1 }{ 4 }\) × Base × Median
(d) Base × Base
Answer
Answer: (b) Base × Altitude
Question 2.
AE is a median to side BC of triangle ABC. If area(ΔABC) = 24 cm, then area(ΔABE) =
(a) 8 cm
(b) 12 cm
(c) 16 cm
(d) 18 cm
Answer
Answer: (b) 12 cm
Question 3.
In the figure, ∠PQR = 90°, PS = RS, QP = 12 cm and QS = 6.5 cm. The area of ΔPQR is
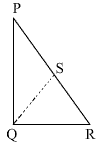
(a) 30 cm2
(b) 20 cm2
(c) 39 cm2
(d) 60 cm2
Answer
Answer: (a) 30 cm2
Question 4.
BCD is quadrilateral whose diagonal AC divides it into two parts, equal in area, then ABCD
ABCD is quadrilateral whose diagonal AC divides it into two parts, equal in area, then ABCD
(a) is a rectangles
(b) is a parallelogram
(c) is a rhombus
(d) need not be any of (a), (b) or (c).
Answer
Answer: (d) need not be any of (a), (b) or (c).
Question 5.
In ΔPQR, if D and E are points on PQ and PR respectively such that DE || QR, then ar (PQE) is equal to
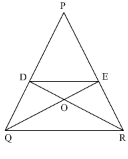
(a) ar (PRD)
(b) ar (DQM)
(c) ar (PED)
(d) ar (DQR)
Answer
Answer: (a) ar (PRD)
Question 6.
If Diagonals AC and BD of a trapezium ABCD with AB || DC intersect each other at O. Then,
(a) ar (AOD) = ar (BOC)
(b) ar (AOD) > ar (BOC)
(c) ar (AOD) < ar (BOC)
(d) None of the above
Answer
Answer: (a) ar (AOD) = ar (BOC)
Question 7.
For two figures to be on the same base and between the same parallels, one of the lines must be.
(a) Making an acute angle to the common base
(b) The line containing the common base
(c) Perpendicular to the common base
(d) Making an obtuse angle to the common base
Answer
Answer: (b) The line containing the common base
Question 8.
Two parallelograms are on equal bases and between the same parallels. The ratio of their areas is:
(a) 1 : 3
(b) 1 : 2
(c) 2 : 1
(d) 1 : 1
Answer
Answer: (d) 1 : 1
Question 9.
If P and Q are any two points lying on the sides DC and AD respectively of a parallelogram ABCD, then:
(a) ar(APB) > ar(BQC)
(b) ar(APB) < ar(BQC)
(c) ar(APB) = ar(BQC)
(d) None of the above
Answer
Answer: (c) ar(APB) = ar(BQC)
Question 10.
A triangle and a rhombus are on the same base and between the same parallels. Then the ratio of area of triangle to that rhombus is:
(a) 1 : 3
(b) 1 : 2
(c) 1 : 1
(d) 1 : 4
Answer
Answer: (b) 1 : 2
Question 11.
Two parallelograms are on equal bases and between the same parallels. The ratio of their areas is
(a) it is 1 : 1.
(b) it is 1 : 2.
(c) it is 3 : 1.
(d) it is 2 : 1.
Answer
Answer: (a) it is 1 : 1.
Question 12.
or two figures to be on the same base and between the same parallels ,they must have a common base and.
(a) One common vertex
(b) The vertices(or the vertex) opposite to the common base lying on a line parallel to the base
(c) The vertices(or the vertex) opposite to the common base lying on a line making an acute angle to the base
(d) Two common vertices
Answer
Answer: (b) The vertices(or the vertex) opposite to the common base lying on a line parallel to the base
Question 13.
The median of a triangle divides it into two
(a) congruent triangles.
(b) isosceles triangles.
(c) right angles.
(d) triangles of equal areas
Answer
Answer: (d) triangles of equal areas
Question 14.
If a triangle and a parallelogram are on the same base and between the same parallels, then the ratio of the area of the triangle to the area of the parallelogram is
(a) it is 1 : 4.
(b) it is 3 : 1.
(c) it is 1 : 2.
(d) it is 1 : 4.
Answer
Answer: (c) it is 1 : 2.
Question 15.
The area of a right triangle is 30 sq cm. If the base is 5 cm, then the hypotenuse must be
(a) 12 cm
(b) 18 cm
(c) 13 cm
(d) 20 cm
Answer
Answer: (c) 13 cm
Question 16.
D,E,F are mid points of the sides BC, CA & AB respectively of ΔABC, then area of BDEF is equal to
(a) \(\frac { 1 }{ 2 }\)ar (ΔABC)
(b) \(\frac { 1 }{ 4 }\)ar (ΔABC)
(c) \(\frac { 1 }{ 3 }\)ar (ΔABC)
(c) \(\frac { 1 }{ 6 }\)ar (ΔABC)
Answer
Answer: (a) \(\frac { 1 }{ 2 }\)ar (ΔABC)
Question 17.
Area of a trapezium, whose parallel sides are 9 cm and 6 cm respectively and the distance between these sides is 8 cm, is
(a) 80 cm2
(b) 30 cm2
(c) 120 cm2
(d) 60 cm2
Answer
Answer: (d) 60 cm2
Question 18.
A median of a triangle divides it into two
(a) Congruent triangles
(b) Isosceles triangles
(c) Right triangles
(d) Equal area triangles
Answer
Answer: (d) Equal area triangles
Hope you found this information on NCERT MCQ Questions for Class 9 Maths Chapter 9 Areas of Parallelograms and Triangles with Answers useful. We are always here to help, so if there is any specific query or question with CBSE Class 9 Maths Areas of Parallelograms and Triangles MCQs Multiple Choice Questions with Answers or any other topic please let us know in the comments below.