These NCERT Solutions for Class 9 Maths Chapter 7 Triangles Ex 7.5 Questions and Answers are prepared by our highly skilled subject experts.
NCERT Solutions for Class 9 Maths Chapter 7 Triangles Exercise 7.5
Question 1.
ABC is a triangle. Locate a point in the interior of ∆ABC which is equidistant from all the vertices of ∆ABC.
Solution:
To locate a point in the interior of ∆ABC which is equidistant from all the vertices of ∆ABC, we take the following steps:
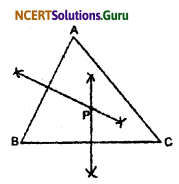
Step I: Draw any triangle ABC.
Step II: Draw perpendicular bisector of side BC and AB.
Step III: Both bisectors intersect each other at point P.
Therefore, P is a point interior of ∆ABC which is equidistant from all the vertices of ∆ABC.
![]()
Question 2.
In a triangle locate a point in its interior which is equidistant from all the sides of the triangle.
Solution:
To locate a point in the interior of the triangle which is equidistant from all the sides of the triangle, we take the following steps:
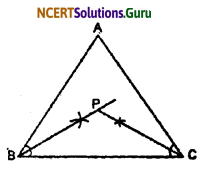
Step I: Draw any triangle ABC.
Step II: Draw angle bisector of ∠B and ∠C.
Step III: Both angle bisectors intersects each other at P.
Therefore, P is the point at which all three sides of ∆ABC are equidistant.
![]()
Question 3.
In a huge park, people are concentrated at three points (see Fig. 7.52).
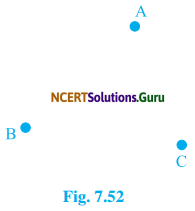
A: Where there are different slides and swings for children.
B: Near which a man-made lake is situated.
C: Which is near to a large parking and exit.
Where should an ice cream parlour be set up so that the maximum number of people can approach it?
Solution:
An ice cream parlour should be set at a point in which A, B, and C are equidistant.
For this we can take the following steps:
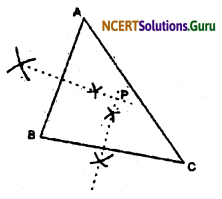
Step I: Join A to B, B to C, and C to A.
Step II: Draw perpendicular bisector of BC and AB.
Step III: Both perpendicular bisectors intersect each other at P.
Therefore, P is the required point, in which ice cream parlour should be set up so that the maximum number of people can approach it.
![]()
Question 4.
Complete the hexagonal and star-shaped Rangolies [see Fig. 7.53 (i) and (ii)] by filling them as many equilateral triangles of side 1 cm as you can. Count the number of triangles in each case. Which has more triangles?
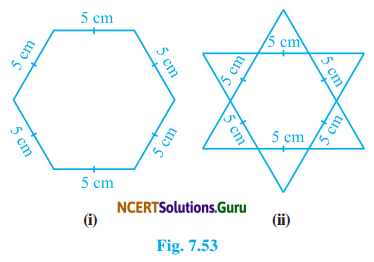
Solution:
Fig. 5.53 (ii) has more equilateral triangles of side 1 cm. As Fig. 7.53 (i) is inside Fig. 7 53 (ii). It is because the area of star-shaped Rangolies is greater than that of hexagonal Rangoli.