These NCERT Solutions for Class 9 Maths Chapter 6 Lines and Angles Ex 6.2 Questions and Answers are prepared by our highly skilled subject experts.
NCERT Solutions for Class 9 Maths Chapter 6 Lines and Angles Exercise 6.2
Question 1.
In Fig. 6.28, find the values of x and y and then show that AB || CD.
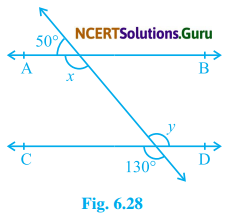
Solution:
According to fig.
50° + x = 180° (Linear pair)
⇒ x = 180° – 50°
⇒ x = 130° …..(i)
Again, x = 130° …..(ii)
(Vertically opposite angles are equal)
From equation (i) and (ii)
x = y (each 130°)
which is the pair of alternate interior angles. And we know that if the pair of alternate interior angles are equal, then the given two lines are parallel.
AB || CD
![]()
Question 2.
In Fig. 6.29, if AB || CD, CD || EF and y : z = 3 : 7, find x.
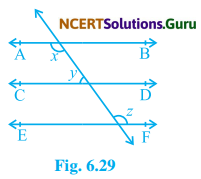
Solution:
We have given AB || CD || EF and y : z = 3 : 7
or, \(\frac{y}{z}=\frac{3}{7}\)
or, y = \(\frac {3}{7}\) z …….(i)
Again AB || EF
∴ x = z ……(ii)
(Pair of alternate interior angle)
Now, AB || CD
∴ x + y = 180°
(Sum of interior angle of the same side of transversal)
z + \(\frac {3}{7}\) z = 180 (∴ x = z and y = \(\frac {3}{7}\) z)
⇒ z = \(\frac{180 \times 7}{10}\)
⇒ z = 126
From, equation (ii)
x = z
or, x = 126
![]()
Question 3.
In Fig. 6.30, if AB || CD, EF || CD and ∠GED = 126°, Find ∠AGE, ∠CEF and ∠FGE.
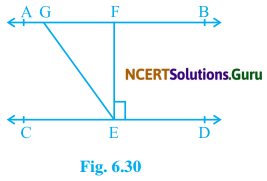
Solution:
We have given AB || CD, EF || CD and ∠GED = 126°
Again ∠GED = ∠AGE (Alternate interior angle)
∠AGE = 126° (i) (∴ Given ∠GED = 126°)
Now, ∠GED = ∠DEF + ∠GEF
⇒ 126 = 90 + ∠GEF (∴ ∠GED = 126 & EF ⊥ CD)
⇒ ∠GEF = 126° – 90° = 36°
Again, ∠AGE + ∠FGE = 180° (Linear pair)
126° + ∠FGE = 180° (From equ. (i) ∠AGE = 126°)
∠FGE = 180° – 126° = 54°
![]()
Question 4.
In Fig. 6.31, if PQ || ST, ∠PQR = 110°, and ∠RST = 130°, find ∠QRS.
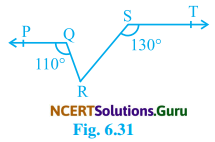
Solution:
We have given that PQ || ST,
∠PQR = 110° and ∠RST = 130°
Construction:
Through R draw a line MN | ST
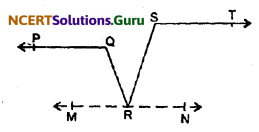
Now, ST || RN (by construction)
Figure
Therefore,
∠RST + ∠SRN = 180° (Sum of interior angle of the same side of transversal)
or, 130° + ∠SRN = 180°
∠SRN = 180° – 130° = 50° ……(i)
Given ∠PQR = 110°
∠QRN = 110°
Again, ∠QRN = ∠QRS + ∠SRN
110 = ∠QRS + 50 (∵ ∠QRN = 110° and ∠SRN = 50° from equ. (i))
∴ ∠QRS = 110° – 50° = 60°
![]()
Question 5.
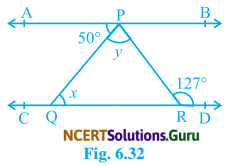
In Fig. 6.32, if AB || CD, ∠APQ = 50° and ∠PRD = 127°, Find x and y.
Solution:
We have given AB || CD
and ∠APQ = 50° & ∠PRD = 127°
Now, AB || CD (given)
∴ ∠APQ = x (Pair of alternate interior angle)
∴ x = 50° (∴ ∠APQ = 50°)
Again, ∠APR = ∠PRD (Pair of alternate interior angles)
∴ ∠APQ = 127°
But, ∠APR = 50° + y
⇒ 127° = 50° + y
⇒ y = 127° – 50°
⇒ y = 77°
![]()
Question 6.
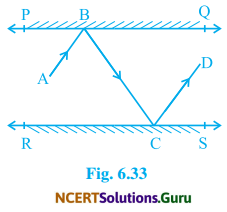
In Fig. 6.33, PQ and RS are two mirrors placed parallel to each other. An incident ray AB strikes the mirror PQ at B, the reflected ray moves along the path BC and strikes the mirror RS at C and again reflects back along CD. Prove that AB || CD.
Solution:
Two plane mirrors PQ and RS such that PQ || RS. An incident ray AB after reflections takes the path BC and CD. BM and CN are the normals to the plane mirror PQ and RS respectively.
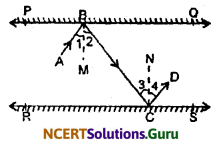
To prove: AB || CD
Proof: Since BM ⊥ PQ, CN ⊥ RS, and PQ || RS
Therefore, CN ⊥ PQ ⇒ BM || CN
Thus, BM and CN are two parallel lines and a transversal BC cuts them at B and C respectively.
∴ ∠2 = ∠3 (Alternate interior angles)
But, ∠1 = ∠2 and ∠3 = ∠4 (By law of reflection)
⇒ ∠1 + ∠2 = ∠2 + ∠2 and ∠3 + ∠4 = ∠3 + ∠3
⇒ ∠1 + ∠2 = 2(∠2) and ∠3 + ∠4 = 2(∠3)
⇒ ∠1 + ∠2 = ∠3 + ∠4 [∵ ∠2 + ∠3 ⇒ 2(∠2) = (∠3)]
∴ ∠ABC = ∠BCD
Thus, lines AB and CD are intersected by transversal BC such that ∠ABC = ∠BCD i.e. alternate interior angles are equal.
Therefore, AB || CD
Hence, AB || CD.