These NCERT Solutions for Class 9 Maths Chapter 2 Polynomials Ex 2.3 Questions and Answers are prepared by our highly skilled subject experts.
NCERT Solutions for Class 9 Maths Chapter 2 Polynomials Exercise 2.3
Question 1.
Find the remainder when x3 + 3x2 + 3x + 1 is divided by
(i) x + 1
(ii) x – \(\frac{1}{2}\)
(iii) x
(iv) x + p
(v) 5 + 2x
Solution:
(i) By long division, we have:

Here, the remainder is 0.
(ii) By long division, we have:
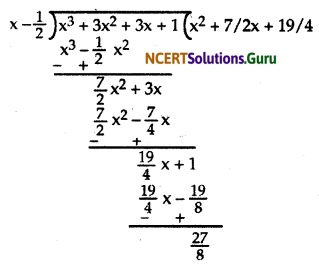
Here, the remainder is \(\frac{27}{8}\)
(iii) By long division, we have

Here, the remainder is 1
![]()
(iv) we have given
x3 + 3x2 + 3x + 1 ÷ x + π
or, x3 + 3x2 + 3x + 1 ÷ x + \(\frac{22}{7}\) (∵ π = \(\frac{22}{7}\))
By long division,

Here, the remainder is \(-\frac{3669}{49}\)
(v) We have given
x3 + 3x2 + 3x + 1 ÷ 5 + 2x
or, x3 + 3x2 + 3x + 1 ÷ 2x + 5
By long division, we have

Here, remainder is \(-\frac{27}{8}\)
Question 2.
Find the remainder when x3 – ax2 + 6x – a is divided by x – a.
Solution:
Here, p(x) = x3 – ax2 + 6x – a, and the zero of x – a is a
So, p(a) = a3 – a(a)2 + 6(a) – a
= a3 – a3 + 6a – a
= 5a
So, 5a is the remainder when x3 – ax + 6x – a is divided by x – a.
![]()
Question 3.
Check whether 7 + 3x is a factor of 3x3 + 7x.
Solution:
We know that 7 + 3x is a factor of 3x3 + 7x only if 7 + 3x divides 3x3 + 7x leaving no remainder.
Here, p(x) = 3x3 + 7x and the zero of 7 + 3x is \(-\frac{7}{3}\). so,
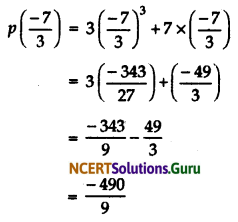
Here, the remainder is \(\frac{-490}{9}\).
Therefore 7 + 3x is not the factor of 3x3 + 7x.