These NCERT Solutions for Class 9 Maths Chapter 12 Heron’s Formula Ex 12.2 Questions and Answers are prepared by our highly skilled subject experts.
NCERT Solutions for Class 9 Maths Chapter 12 Heron’s Formula Exercise 12.2
Question 1.
A park in the shape of quadrilateral ABCD, has ∠C = 90°, AB = 9 m, BC = 12 m, CD = 5 m and AD = 8 m. How much area does it occupy?
Solution:
In ABCD,
CD = 5 cm, BC = 12 and ∠C = 90°
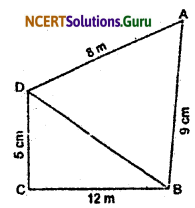
∴ By pythagoras theorem we know that
h2 = P2 + b2
⇒ BD2 = CD2 + BC2
⇒ BD2 = 52 + 122
⇒ BD2 = 169
⇒ BD = √169 = 13 cm.
Area of triangle BCD = \(\frac {1}{2}\) × 12 × 5 = 30 cm.
In ∆ABD,
AD = 8 m, AB = 9 m, and BD = 13 cm
∴ s = \(\frac{8+9+13}{2}\) = 15
∴ By Heron’s formula we know that
Area of triangle
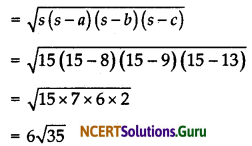
= 35.5 m2 (approx)
Now,
Area perpendicular ABCD = Ar ΔBCD + Ar ΔABD
= 30 + 35.5
= 65.5 m2 (approx)
Therefore, quadrilateral ABCD occupy 65.5 m2 area.
![]()
Question 2.
Find the area of a quadrilateral ABCD in which AB = 3 cm, BC = 4 cm, CD = 4 cm, DA = 5 cm and AC = 5 cm.
Solution:
In ΔABC,
AB = 3 cm, BC = 4 cm and AC = 5 cm
∴ s = \(\frac{3+4+5}{2}\) = 6
∴ By Heron’s formula we know that
Area of ΔABC
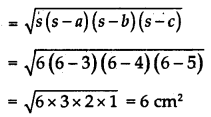
Again in ΔACD,
AC = 5 cm, AD = 5 cm, and CD = 4 cm
∴ s = \(\frac{5+5+4}{2}\) = 7
∴ By Heron’s formula we know that,
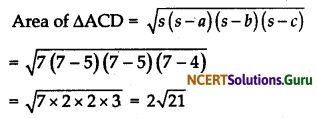
= 9.2 cm2 (approx)
∴ Area of quadrilateral ABCD = Ar ΔABC + Ar ΔACD
= 6 + 9.2
= 15.2 cm2 (approx)
![]()
Question 3.
Radha made a picture of an aeroplane with coloured paper .is shown in Fig. 12.15. Find the total area of the paper used.
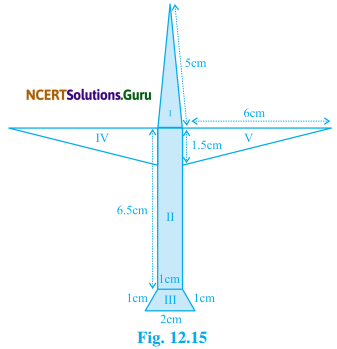
Solution:
In part I, sides of triangle are 5 cm, 5 cm and 1 cm
∴ s = \(\frac{5+5+1}{2}\) = 5.5
∴ By Heron’s formula
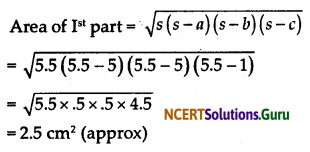
The area of the IInd part which is in the form of the rectangle is
6.5 × 1 = 6.5 cm2 (Area of rectangle = l × b)
Area of IIIrd part = 3 × \(\frac{\sqrt{3}}{4}\) cm = 1.3 cm2 (approx)
Area of IVth part, which is in the form of triangle is = \(\frac {1}{2}\) × 15 × 6 = 4.5 cm2
Area of Vth part, which is also in Hie form of triangle is = \(\frac {1}{2}\) × 15 × 6 = 4.5 cm2
Therefore, total area of the paper used = 2.5 + 6.5 +1.3 + 4.5 + 4.5 = 19.3 cm2 (approx)
Question 4.
A triangle and a parallelogram have the same base and the same area. If the sides of the triangle are 26 cm, 28 cm, and 30 cm, and the parallelogram stands on the base 28 cm, find the height of the parallelogram.
Solution:
Sides of triangle are 26 cm, 28 cm and 30 cm.
∴ s = \(\frac{26+28+30}{2}\) = 42
∴ By Heron’s formula we know that
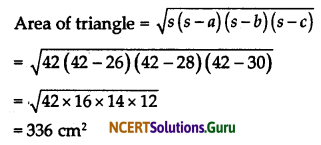
According to question,
Area of parallelogram = Area of triangle
Base × altitude = 336
28 × altitude = 336
∴ Altitude = \(\frac{336}{28}\) = 12
∴ Height of the parallelogram stands on the base 28 cm is 12 cm.
![]()
Question 5.
A rhombus-shaped field has green grass for 18 cows to graze. If each side of the rhombus is 30 m and its longer diagonal is 48 m, how much rea of grass field will each cow be getting.
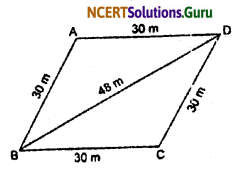
Solution:
In ∆ABD
AB = 30 m, AD = 30 m and BD = 48 m.
∴ s = \(\frac{30+30+48}{2}\) = 54
∴ By Heron’s formula we know that
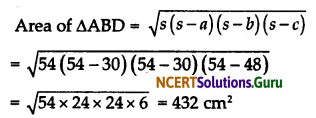
∴ Area of rhombus ABCD = 2 × 432 = 864 m2
Therefore, area of grass getting by each cow = \(\frac{864}{18}\) = 48 m2
Question 6.
An umbrella is made by stitching 10 triangular pieces of cloth of two different colours (see Fig. 12.16), each piece measuring 20 cm, 50 cm, and 50 cm. How much cloth of each colour is required for the umbrella?
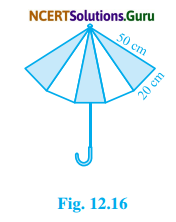
Solution:
For one triangular piece,
∴ s = \(\frac{20+50+50}{2}\) = 60
∴ By Heron’s formula
Area of one triangular piece
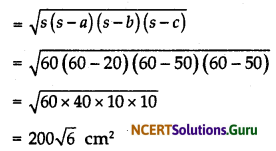
Therefore,
Area of five triangular piece = 5 × 200√6 = 1000√6 cm2
Hence, clothes of each colour are required for the umbrella is 1000√6 cm2.
![]()
Question 7.
A kite in the shape of a square with a diagonal 32 cm and art isosceles triangle of base S cm and sides 6 cm each is lobe made of three diffident shades as shown in Fig. 12.17. How much paper of each shade has been used in it?
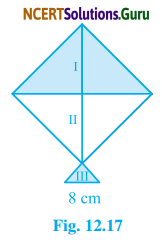
Solution:
We have given that, the shape of a kite is square and length of its diagonal is 32 cm.
Area of 1 triangular region
= \(\frac {1}{2}\) × base × height
= \(\frac {1}{2}\) × 32 × 16
= 256 cm2
(∵ We know that diagonals of square bisects each other at 90°)
Now, Area of IInd triangular region
= \(\frac {1}{2}\) × base × height
= \(\frac {1}{2}\) × 32 × 16
= 256 cm2
Again, we have given that IIIrd part of the given kite is in the shape of an isosceles triangle whose equal sides are 6 cm and the base is 8 cm.
s = \(\frac{a+b+c}{2}\)
= \(\frac{6+6+8}{2}\)
= 10
∴ By Heron’s formula,
Area of IIIrd triangular region
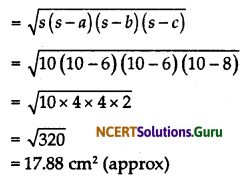
![]()
Question 8.
A floral design on a floor is made up of 16 tiles which are triangular, the sides of the triangle being 9 cm, 28 cm, and 35 cm (see Fig. 12.18). Find the cost of polishing the tiles at the rate of 50 p per cm2.

Solution:
The sides of one triangular tile are 9 cm, 28 cm, and 35 cm
s = \(\frac{9+28+35}{2}\) = 36 cm
By Heron’s formula, we know that
Area of one triangular tile
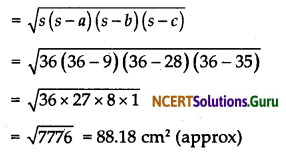
Therefore, area of 16 triangular tiles = 88.18 × 16 = 1410.88 cm2
Hence, the cost of polishing at the rate of 50 p per cm2 is 1410.88 × 0.50 = Rs. 705.44 (approx)
![]()
Question 9.
A field is in the shape of a trapezium whose parallel sides are 25 m and 10 m. The non-parallel sides are 14 m and 13 m. Find the area of the field.
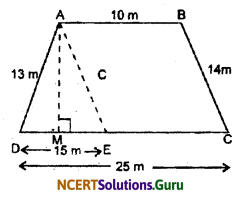
Solution:
Draw a line through A and parallel to BC cut CD at E. Again draw AM ⊥ CD.
Now, sides of ∆ADE are 13 m, 15 m and 14 m
s = \(\frac{13+14+15}{2}=\frac{42}{2}\) = 21 m
By Heron’s formula, we know that
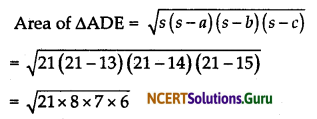
But, Area of ∆ADE = \(\frac {1}{2}\) × DE × AM
or, 84= \(\frac {1}{2}\) × 15 × AM
or, AM = \(\frac{84 \times 2}{15}\) = 11.2 m
We know that
Area of trapezium
= \(\frac {1}{2}\) × (25 + 10) × 11.2
= \(\frac {1}{2}\) × 35 × 11.2
= 196 m2