These NCERT Solutions for Class 9 Maths Chapter 11 Constructions Ex 11.1 Questions and Answers are prepared by our highly skilled subject experts.
NCERT Solutions for Class 9 Maths Chapter 11 Constructions Exercise 11.1
Question 1.
Construct an angle of 90° at the initial point of a given ray and justify the construction.
Solution:
Steps of construction:
1. Draw a straight line AB.
2. Taking A as centre, draw an arc, which intersects AB at a point D.
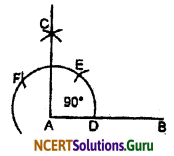
3. Now, taking D as a centre, the same radius AD, intersect at E and F on the succession arc. (here AD = \(\widehat{\text { DE }}\) = \(\widehat{\text { EF }}\))
4. From point E take a radius (which should be greater than \(\frac {1}{2}\) \(\widehat{\text { EF }}\)) then with the same radius from F intersect the arc at point C.
5. Now, join C to A.
6. The required angle ∠ABC = 90°.
![]()
Question 2.
Construct an angle of 45° at the initial point of a given ray and justify the construction.
Solution:
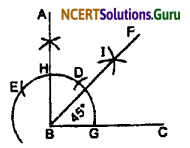
Steps of Constructions:
1. Follow the instruction of the previous question upto ∠ABC = 90°.
2. Take an arc from the points H and G each which Intersect at I.
3. Here ∠FBC is half of ∠ABC, FB is the angle bisector.
4. So, the required ∠FBC = 45°
Question 3.
Construct the angles of the following measurements:
(i) 30°
(ii) 22½°
(iii) 15°
Solution:
(i) Steps of Construction:
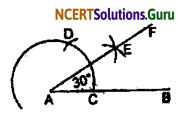
1. Take a straight line AB.
2. Draw an arc, taking A as centre which intersects AB at C.
3. From C take another arc \(\widehat{\mathrm{CD}}\) such that AB = \(\widehat{\mathrm{CD}}\)
4. From C and D take similar arc which intersects at E.
5. The required ∠FAB = 30°.
(ii) Steps of construction:
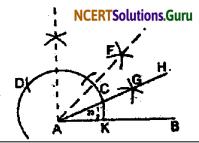
1. Follow the instruction of question (2) i.e. ∠FAB = 45°.
2. Take the same arc from points C and K, intersect at G.
3. The required ∠HAB = 22½°
(iii) Step of construction:
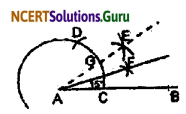
1. Follow the instruction of 3:
(i) ∠EAB = 30°.
2. Take a small arc from the points G and C that intersects at F.
3. The required angle ∠FAB = 15°.
![]()
Question 4.
Construct the following angles and verify by measuring them by a protractor:
(i) 75°
(ii) 105°
(iii) 135°.
Solution:
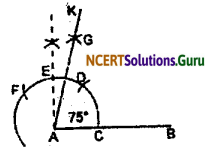
(i) Steps of construction:
1. Follow as in question 1. i.e. ∠EAC = 90°.
2. Take the same arc from points D and E which intersect at G.
3. The required ∠KAB = 75°.
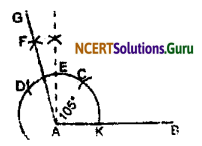
(ii) Steps of construction:
1. Follow the instruction as in the previous question upto ∠EAB = 90°.
2. Take the same arc from points D and E intersect at F.
3. Join F to A.
4. The required ∠GAB = 105°.
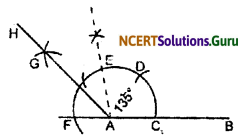
(iii) Steps of construction:
1. Follow the instruction as ∠EAB = 90°.
2. Take the same arc from the points E and F, Intersect at G.
3. Join G to A.
4. The required ∠HAB = 135°.
![]()
Question 5.
Construct an equilateral triangle, given its side, and justify the construction.
Solution:
Steps of construction:
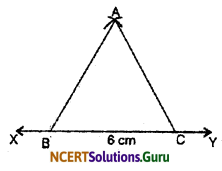
1. Take a straight line XY.
2. By measuring 6 cm on the scale, cut one point C on XY line the reverse the same to get B point. Here, BC = 6 cm
3. From B and C points draw an arc of the same length intersect at A.
4. We find here AB = BC = CA = 6 cm. Thus ABC is an equilateral triangle.