These NCERT Solutions for Class 9 Maths Chapter 1 Number Systems Ex 1.6 Questions and Answers are prepared by our highly skilled subject experts.
NCERT Solutions for Class 9 Maths Chapter 1 Number Systems Exercise 1.6
Question 1.
Find
(i) \(64^{\frac{1}{2}}\)
(ii) \(32^{\frac{1}{5}}\)
(iii) \(125^{\frac{1}{3}}\)
Solution:
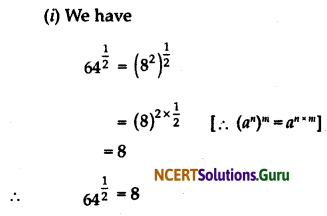
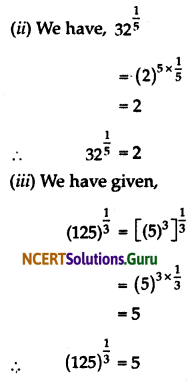
Question 2.
Find
(i) \(9^{\frac{3}{2}}\)
(ii) \(32^{\frac{2}{5}}\)
(iii) \(16^{\frac{3}{4}}\)
(iv) \((125)^{-\frac{1}{3}}\)
Solution:
(i) We have given
\(9^{\frac{3}{2}}=\left[(9)^{\frac{1}{2}}\right]^{3}\)
= (3)3
= 27
Therefore, \((9)^{\frac{3}{2}}\) = 27
![]()
(ii) We have given,
\(32^{\frac{2}{5}}=\left[32^{\frac{1}{5}}\right]^{2}\)
= (2)2
= 4
Therefore, \((32)^{\frac{2}{5}}\) = 4
(iii) We have given,
\((16)^{\frac{3}{4}}=\left[(16)^{\frac{1}{4}}\right]^{3}\)
= (2)3
= 8
Therefore, \((16)^{3 / 4}\) = 8
(iv) We have given,
\((125)^{-\frac{1}{3}}=\left[(125)^{\frac{1}{3}}\right]^{-1}\)
= (5)-1
= \(\frac{1}{5}\)
Therefore, \((125)^{-\frac{1}{3}}=\frac{1}{5}\)
![]()
Question 3.
Simplify
(i) \(2^{\frac{2}{3}} \cdot 2^{\frac{1}{5}}\)
(ii) \(\left(\frac{1}{3^{3}}\right)^{7}\)
(iii) \(\frac{11^{\frac{1}{2}}}{11^{\frac{1}{4}}}\)
(iv) \(7^{\frac{1}{2}} \cdot 8^{\frac{1}{2}}\)
Solution:
(i) We have given \(2^{\frac{2}{3}} \cdot 2^{\frac{1}{5}}\)

