These NCERT Solutions for Class 9 Maths Chapter 1 Number Systems Ex 1.3 Questions and Answers are prepared by our highly skilled subject experts.
NCERT Solutions for Class 9 Maths Chapter 1 Number Systems Exercise 1.3
Question 1.
Write the following in decimal form and say what kind of decimal expansion each has:
(i) \(\frac{36}{100}\)
(ii) \(\frac{1}{11}\)
(iii) \(4 \frac{1}{8}\)
(iv) \(\frac{3}{13}\)
(v) \(\frac{2}{11}\)
(vi) \(\frac{329}{400}\)
Solution:
(i) By actual division we have
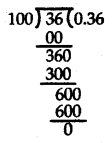
The decimal form of \(\frac{36}{100}\) is 0.36
Here, the remainder becomes 0, therefore it has a terminating decimal expansion.
(ii) By actual division we have
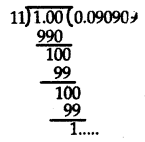
The decimal form of \(\frac{1}{11}\) is 0.090909….. of \(0 . \overline{09}\).
Hence remainder never becomes zero but repeats. Therefore, it has non terminating but repeating decimal expansion.
![]()
(iii) \(4 \frac{1}{8}\)
We can also write \(\frac{33}{8}\)
By actual division we have,

The decimal form of \(4 \frac{1}{8}\) is 4.125.
Here remainder becomes zero after certain steps. Therefore it has a terminating decimal expansion.
(iv) By actual division we have
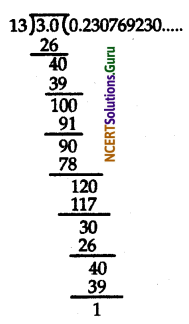
The decimal form of \(\frac{3}{13}\) is 0.2307692307….. or \(0 . \overline{230769}\).
Here, the remainder never becomes zero but repeats after some steps.
Therefore, it has a non terminating but repeating decimal expansion.
![]()
(v) By actual division we have

The decimal form of \(\frac{2}{11}\) is 0.181818…. or \(0 . \overline{18}\). Here remainder never becomes zero but repeat after some steps.
Therefore, it has non terminating but repeating decimal expansion.
(vi) By actual division we have,

The decimal form of \(\frac{329}{400}\) is 0.8225. Here remainder becomes zero after some steps. Therefore, it has terminating decimal expansion.
![]()
Question 2.
You know that \(\frac{1}{7}=0 . \overline{142857}\). Can you predict what the decimal expansions of \(\frac{2}{7}, \frac{3}{7}, \frac{4}{7}, \frac{5}{7}, \frac{6}{7}\) are, without actually doing the long devision? If so how?
Solution:
We have given that
\(\frac{1}{7}=0 . \overline{142857}\)

Question 3.
Express the following in the form \(\frac {p}{q}\), where p and q are integers and q ≠ 0.
(i) \(0 . \overline{6}\)
(ii) \(0 . \overline{47}\)
(iii) \(0 . \overline{001}\)
Solution:
Let x = \(0 . \overline{6}\)
or, x = 0.66666…… (i)
Now, add 6 both side in equation (i)
x + 6 = 0.66666…… + 6
or x + 6 = 6.6666……. (ii)
Again, multiply 10 both side in equation (i)
10x = 0.66666…. × 10
or, 10x = 6.6666…. (iii)
Now, from equation (ii) and (iii)
x + 6 = 10x
9x = 6
∴ x = \(\frac{6}{9}\)
Therefore, \(0 . \overline{6}\) = x = \(\frac{2}{3}\)
![]()
(ii) Let x = \(0.4 \overline{7}\)
or x = 0.47777……. (i)
Now, multiply 10 both side in equation (i)
10x = 0.47777……. × 10
or, 10x = 4.77777…… (ii)
Again, multiply 100 both side in equation (i)
100x = 0.47777 × 100
or, 100x = 4.77777…….. (iii)
Subtract equation (ii) from equation (iii)
90x = 43.0000
or 90x = 43
∴ x = \(\frac{43}{90}\)
Therefore, \(0.4 \overline{7}\) = x = \(\frac{43}{90}\)
which is in the form of \(\frac {p}{q}\)
(iii) Let x = \(0 . \overline{001}\)
or, x = 0.001001001……. (i)
Now, add 1 both side in equation (i)
x + 1 = 0.001001001…… + 1
or x + 1 = 1.001001001……. (ii)
Again, multiply 1000 both side in equation (i)
1000 × x = 1000 × 0.001001001……..
or, 1000x = 1.001001001….. (iii)
From equation (ii) and (iii) we get
x +1 = 1000x
or 999x = 1
or x = \(\frac{1}{999}\)
Therefore, \(0 . \overline{001}=x \times \frac{1}{999}\)
which is in the form of \(\frac {p}{q}\)
![]()
Question 4.
Express 0.99999…… in the form \(\frac {p}{q}\). Are you surprised by your answer? With your teacher and classmates discuss why the answer makes sense.
Solution:
Let x = 0.9999…… (i)
Add 9 both side in equation (i)
x + 9 = 9 + 0.99999………
or, x + 9 = 9.99999…… (ii)
Again, multiply 10 both side in equation (i)
10x = 9.9999……. (iii)
From equation (ii) and (iii) we get
10x = x + 9
or, 9x = 9
or, x = 1
Therefore, 0.9999…… = 1
It is because there is infinite 9 comes after the point; which is very-very close to 1.
Question 5.
What can the maximum number of digits be in the repeating block of digits in the decimal expansion of \(\frac{1}{17}\)? Perform the division to check your answer.
Solution:
By actual division we have
It is clear that, \(\frac{1}{17}=0 . \overline{0588235294117647}\)
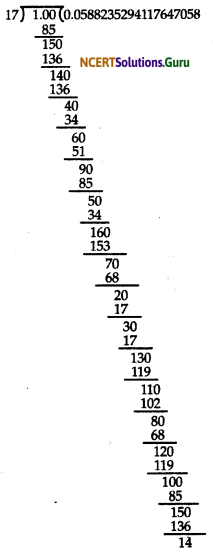
It is clear that, \(\frac{1}{17}=0 . \overline{0588235294117647}\)
So, the maximum number of digits be in the repeating block of digits in die decimal expansion of \(\frac{1}{17}\) is 16.
![]()
Question 6.
Look at several examples of rational numbers in the form \(\frac{p}{q}\) (q ≠ 0), where p and q are integers with no common factors other than 1 and having terminating decimal representations (expansions). Can you guess what property q must satisfy?
Solution:
Some examples of a rationed number having terminating decimal representations are:
(i) \(\frac{1}{2}\) = 0.5
(ii) \(\frac{7}{4}\) = 1.75
(iii) \(\frac{7}{8}\) = 0.875
(iv) \(\frac{2}{5}\) = 0.4
It is clear that the prime factorization of q has only power of 2 or power of 5 or both.
Question 7.
Write three numbers whose decimal expansions are non-terminating non-recurring.
Solution:
We knew that the decimal expansions of an irrational number are non-terminating non-recurring. Three examples of such numbers are:
√2 = 1.4142135…….
√3 = 1.732050807………
π = 3.1415926535………
![]()
Question 8.
Find three different irrational numbers between the rational numbers \(\frac{5}{7}\) and \(\frac{9}{11}\).
Solution:
To find an irrational numbers between \(\frac{5}{7}\) and \(\frac{9}{11}\) is non terminating non recurring lying between them.
Here, \(\frac{5}{7}=0 . \overline{714285}\) and \(\frac{9}{11}=0 . \overline{81}\)
Therefore, the required three different irrational number which is lying between \(\frac{5}{7}\) and \(\frac{9}{11}\) are 0.720720072000…….., 0.730730073000……., and 0.740740074000………
Question 9.
Classify the following number as rational or irrational:
(i) √23
(ii) √225
(iii) 0.3796
(iv) 7.478478…….
(v) 1.101001000100001…….
Solution:
(i) We have
√23 = 4.795831523……..
It is non-terminating non-recurring.
So, √23 is an irrational number
(ii) We have
√225 = 15
or √225 = \(\frac{15}{1}\)
which is a rational number
![]()
(iii) We have,
0.3796 = \(\frac{3796}{10000}\)
which is in the form of \(\frac{p}{q}\)
So, 0.3796 is a rational number.
(iv) We have
7.478478……. = \(7 . \overline{478}\) which is non terminating recurring.
Therefore, 7.478478…….. is an irrational number.
(v) We have, 1.101001000100001……..
which is non-terminating non-recurring.
Therefore, 1.101001000100001……… is an irrational number.