These NCERT Solutions for Class 6 Maths Chapter 3 Playing With Numbers Ex 3.3 Questions and Answers are prepared by our highly skilled subject experts.
NCERT Solutions for Class 6 Maths Chapter 3 Playing With Numbers Exercise 3.3
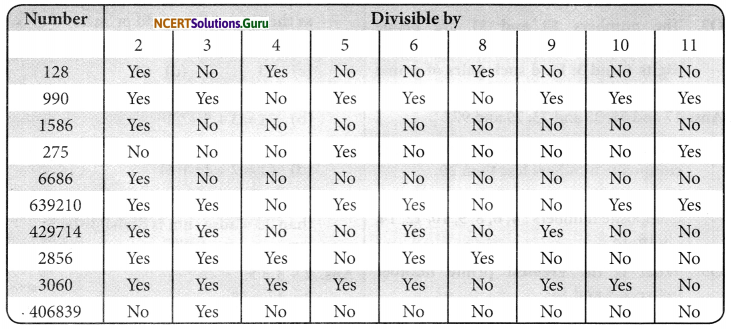
Question 1.
Using divisibility tests, determine which of the following numbers are divisible by 2; by 3; by 4; by 5; by 6; by 8; by 9; by 10; by 11 (say, yes or no):
Answer:
![]()
Question 2.
Using divisibility tests, determine which of the following numbers are divisible by 4; by 8:
(a) 572
(b) 726352
(c) 5500
(d) 6000
(e) 12159
(f) 14560
(g) 21084
(h) 31795072
(i) 1700
(j) 2150
Answer:
(a) 572
→ Divisible by 4 as its last two digits are divisible by 4.
→ Not divisible by 8 as its last three digits are not divisible by 8.
(b) 726352
→ Divisible by 4 as its last two digits are divisible by 4.
→ Divisible by 8 as its last three digits are divisible by 8.
(c) 5500
→ Divisible by 4 as its last two digits are divisible by 4.
→ Not divisible by 8 as its last three digits are not divisible by 8.
(d) 6000
→ Divisible by 4 as its last two digits are 0.
→ Divisible by 8 as its last three digits are 0.
(e) 12159
→ Not divisible by 4 and 8 as it is an odd number.
(f) 14560
→ Divisible by 4 as its last two digits are divisible by 4.
→ Divisible by 8 as its last three digits are divisible by 8.
(g) 21084
→ Divisible by 4 as its last two digits are divisible by 4.
→ Not divisible by 8 as its last three digits are not divisible by 8.
(h) 31795072
→ Divisible by 4 as its last two digits are divisible by 4.
→ Divisible by 8 as its last three digits are divisible by 8.
![]()
(i) 1700
→ Divisible by 4 as its last two digits are 0.
→ Not divisible by 8 as its last three digits are not divisible by 8.
(j) 2150
→ Not divisible by 4 as its last two digits are not divisible by 4.
→ Not divisible by 8 as its last three digits are not divisible by 8.
Question 3.
Using divisibility tests, determine which of following numbers are divisible by 6:
(a) 297144
(b) 1258
(c) 4335
(d) 61233
(e) 901352
(f) 438750
(g) 1790184
(h) 12583
(i) 639210
(j) 17852
Answer:
(a) 297144
→ Divisible by 2 as its unit’s place is an even number.
→ Divisible by 3 as sum of its digits (= 27) is divisible by 3.
Since the number is divisible by both 2 and 3, therefore, it is also divisible
(b) 1258
→ Divisible by 2 as its units place is an even number.
→ Not divisible by 3 as sum of its digits (= 16) is not divisible by 3.
Since the number is not divisible by both 2 and 3, therefore, it is not divisible by 6.
(c) 4335
→ Not divisible by 2 as its unit’s place is not an even number.
→ Divisible by 3 as sum of its digits (= 15) is divisible by 3.
Since the number is not divisible by both 2 and 3, therefore, it is not divisible by 6.
(d) 61233
→ Not divisible by 2 as its unit’s place is not an even number.
→ Divisible by 3 as sum of its digits (= 15) is divisible by 3.
Since the number is not divisible by both 2 and 3, therefore, it is not divisible by 6.
(e) 901352
→ Divisible by 2 as its unit’s place is an even number.
→ Not divisible by 3 as sum of its digits (= 20) is not divisible by 3.
Since the number is not divisible by both 2 and 3, therefore, it is not divisible by 6.
![]()
(f) 438750
→ Divisible by 2 as its unit’s place is an even number.
→ Divisible by 3 as sum of its digits (= 27) is divisible by 3.
Since the number is divisible by both 2 and 3, therefore, it is divisible by 6.
(g) 1790184
→ Divisible by 2 as its unit’s place is an even number.
→ Divisible by 3 as sum of its digits (= 30) is divisible by 3.
Since the number is divisible by both 2 and 3, therefore, it is divisible by 6.
(h) 12583
→ Not divisible by 2 as its unit’s place is not an even number.
→ Not divisible by 3 as sum of its digits (= 19) is not divisible by 3.
Since the number is not divisible by both 2 and 3, therefore, it is not divisible by 6.
(i) 639210
→ Divisible by 2 as its unit’s place is an even number.
→ Divisible by 3 as sum of its digits (= 21) is divisible by 3.
Since the number is divisible by both 2 and 3, therefore, it is divisible by 6.
(j) 17852
→ Divisible by 2 as its units place is an even number.
→ Not divisible by 3 as sum of its digits (= 23) is not divisible by 3.
Since the number is not divisible by both 2 and 3, therefore, it is not divisible by 6.
Question 4.
Using divisibility tests, determine which of the following numbers are divisible by 11:
(a) 5445
(b) 10824
(c) 7138965
(d) 70169308
(e) 10000001
(f) 901153
Answer:
(a) 5445
Sum of the digits at odd places =4+5=9
→ Sum of the digits at even places =4+5=9
→ Difference of both sums = 9-9 = 0 Since the difference is 0, therefore, the number is divisible by 11.
(b) 10824
→ Sum of the digits at odd places = 4 + 8 +1 = 13
→ Sum of the digits at even places =2+0=2
→ Difference of both sums = 13 – 2 = 11 Since the difference is 11, therefore, the number is divisible by 11.
(c) 7138965
→ Sum of the digits at odd places = 5 + 9 + 3 + 7 = 24
→ Sum of the digits at even places = 6 + 8 + 1 = 15
→ Difference of both sums = 24 – 15 = 9
Since the difference is neither 0 nor 11, therefore, the number is not divisible by 11.
![]()
(d) 70169308
→ Sum of the digits at odd places = 8 + 3 + 6 + 0 = 17
→ Sum of the digits at even places = 0 + 9 + 1 + 7 = 17
→ Difference of both sums = 17 – 17 = 0
Since the difference is 0, therefore, the number is divisible by 11.
(e) 10000001
→ Sum of the digits at odd places
= 1 + 0 + 0 + 0 = 1
→ Sum of the digits at even places
= 0 + 0 + 0 + 1 = 1
→ Difference of both sums =1-1=0 Since the difference is 0, therefore, the number is divisible by 11.
(f) 901153
Sum of the digits at odd places = 3 + 1 +0 = 4
→ Sum of the digits at even places = 5 + 1 + 9 = 15
→ Difference of both sums =15 – 4 = 11
Since the difference is 11, therefore, the number is divisible by 11.
Question 5.
Write the smallest digit and the greatest digit in the blanks space of each of the following numbers so that the number formed is divisibly by 3:
(a) ………………. 6724
(b) 4765 ………………. 2
Answer:
(a) We know that a number is divisible by 3 if the sum of all digits is divisible by 3.
Therefore, Smallest digit: 2 → 26724 = 2 + 6 + 7 + 2 + 4 = 21
Largest digit: 8 → 86724 = 8 + 6 + 7 + 2 + 4 = 27
(b) We know that a number is divisible by 3 if the sum of all digits is divisible by 3.
Therefore, Smallest digit: 0 → 476502 =4+7+6+5+0+2=24
Largest digit: 9 → 476592 = 9 + 4 + 7 + 6 + 5 + 0 + 2 = 33
Question 6.
Write a digit in the blank space of each of the following numbers so that the number formed is divisibly by 11:
(a) 92 …………… 389
(b) 8 ……………….. 9484
Answer:
(a) We know that a number is divisible by 11 if the difference of the sum of the digits at odd places and that of even places should be either 0 or 11.
Therefore, 928389 →
Odd places = 9 + 8 + 8 = 25
Even places = 2 + 3 + 9 = 14
Difference = 25 – 14 = 11
![]()
(b) We know that a number is divisible by 11 if the difference of the sum of the digits at odd places and that of even places should be either 0 or 11.
Therefore, 869484 →
Odd places = 8 + 9 + 8 = 25
Even places = 6 + 4 + 4 = 14
Difference = 25 – 14 = 11