These NCERT Solutions for Class 6 Maths Chapter 12 Ratio and Proportion Ex 12.1 Questions and Answers are prepared by our highly skilled subject experts.
NCERT Solutions for Class 6 Maths Chapter 12 Ratio and Proportion Exercise 12.1
Question 1.
There are 20 girls and 15 boys in a class.
(a) What is the ratio of number of girls to the number of boys?
(b) What is the ratio of number of girls to the total number of students in the class?
Answer:
(a) The ratio of girls to that of boys = \(\frac{20}{15}=\frac{4}{3}\) = 4 : 3
(b) The ratio of girls to total students = \(\frac{20}{20+15}=\frac{20}{35}=\frac{4}{7}\) = 4 : 7
![]()
Question 2.
Out of 30 students in a class, 6 like football, 12 like cricket and remaining like tennis. Find the ratio of
(a) Number of students liking football to number of students liking tennis.
(b) Number of students liking cricket to total number of students.
Answer:
Total number of students = 30
Number of students like football = 6
Number of students like cricket = 12
Thus number of students like tennis = 30 – 6 – 12 = 12
(a) The ratio of students like football that of tennis = \(\frac{6}{12}=\frac{1}{2}\) = 1 : 2
(b) The ratio of students like cricket to that of total students = \(\frac{12}{30}=\frac{2}{5}\) = 2.5
Question 3.
See the figure and find the ratio of
(a) Number of triangles to the number of circles inside the rectangle.
(b) Number of squares to all the figures inside the rectangle.
(c) Number of circles to all the figures inside the rectangle.
Answer:
(a) Ratio of number of triangle to that of circles = \(\frac{3}{2}\) = 3 : 2
(b) Ratio of number of squares to all figures = \(\frac{2}{7}\) = 2 : 7
(c) Ratio of number of circles to all figures = \(\frac{2}{7}\) = 2 : 7
![]()
Question 4.
Distances travelled by Hamid and Akhtar in an hour are 9 km and 12 km. Find the ratio of speed of Hamid to the speed of Akhtar.
Answer:
We know that, Speed = \(\frac{\text { Distance }}{\text { Time }}\)
Speed of Hamid = \(\frac{9 \mathrm{~m}}{1 \mathrm{~h}}\) = 9 km/h and Speed of Akhtar \(\frac{12 \mathrm{~m}}{1 \mathrm{~h}}\) = 12 km/h
Ratio of speed of Hamid to that of speed of Akhtar = \(\frac{9}{12}=\frac{3}{4}\) = 3 : 4
Question 5.
Fill in the following blanks:
Answer:
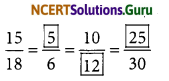
Yes, these are equivalent ratios.
Question 6.
Find the ratio of the following:
(a) 81 to 108
(b) 98 to 63
(c) 33 km to 121 km
(d) 30 minutes to 45 minutes
Answer:
(a) Ratio of 81 to 108
= \(\frac{81}{108}=\frac{3}{4}\) = 3 : 4
(b) Ratio of 98 to 63
= \(\frac{98}{63}=\frac{14}{9}\) = 14 : 9
(c) Ratio of 33 km to 121 km
= \(\frac{33}{121}=\frac{3}{11}\) = 3 : 11
(d) Ratio of 30 minutes to 45 minutes
= \(\frac{30}{45}=\frac{2}{3}\) = 2 : 3
![]()
Question 7.
Find the ratio of the following:
(a) 30 minutes to 1.5 hours
(b) 40 cm to 1.5 m
(c) 55 paise to ₹ 1
(d) 500 mL to 2 litres
Answer:
(a) 30 minutes to 1.5 hour
1.5 hours = 1.5 × 60 = 90 minutes
[∵ 1 hour = 60 minutes]
Now, ratio of 30 minutes to 1.5 hour = 30 minutes: 1.5 hour
⇒ 30 minutes : 90 minutes
= \(\frac{30}{90}=\frac{1}{3}\) = 1 : 3
(b) 40 cm to 1.5 m
1.5 m = 1.5 × 100 cm = 150 cm
[∵ 1 m = 100 cm]
Now. ratio of 40 cm to 1.5 m
= 40 cm : 1.5 m
⇒ 40 cm : 150 cm
= \(\frac{40}{150}=\frac{4}{15}\) = 4 : 15
(c) 55 paise to ₹ 1
Rs 1 = 100 paise
Now, ratio of 55 paise to ₹ 1
= 55 paise : 100 paise
⇒ \(\frac{55}{100}=\frac{11}{20}\) = 11 : 20
(d) 500 ml to 2 litters
2 litres = 2 × 1000 ml = 2000 ml
[∵ litre = 1000 ml]
Now, ratio of 500 ml to 2 litres
= 500 m 1 : 2 litres
⇒ 500 ml : 2000 ml
= \(\frac{500}{2000}=\frac{1}{4}\) = 1 : 4
Question 8.
In a year, Seema earns ₹ 1, 50, 000 and saves ₹ 50,000. Find the ratio of
(a) Money that Seema earns to the money she saves.
(b) Money that she saves to the money she spends.
Answer:
Total earning
= ₹ 1,50,000 and Saving = ₹ 50,000
∵ Money spent
= ₹ 1,50,000 – ₹ 50,000 = ₹ 1,00,000
(a) Ratio of money earned to money
saved = \(\frac{150000}{50000}=\frac{3}{1}\) = 3 : 1
(b) Ratio of money saved to money
spend = \(\frac{50000}{100000}=\frac{1}{2}\) = 1 : 2
![]()
Question 9.
There are 102 teachers in a school of 3300 students. Find the ratio of the number of teachers to the number of students.
Answer:
Ratio of number of teachers to that of studends = \(\frac{102}{3300}=\frac{17}{550}\) = 17 : 550
Question 10.
In a college, out of 4320 students, 2300 are girls. Find the ratio of
(a) Number of girls to the total number of students.
(b) Number of boys to the number of girls.
(c) Number of boys to the total number of students.
Answer:
Total number of students in school = 4320
Number of girls = 2300
Therefore, number of boys = 4320 – 2300 – 2020
(a) Ratio of girls to total number of students = \(\frac{2300}{4320}=\frac{115}{216}\) = 115 : 216
(b) Ratio of boys to that of girls = \(\frac{2020}{2300}=\frac{101}{115}\) = 101 : 115
(c) Ratio of boys to total number of students = \(\frac{2020}{4320}=\frac{101}{216}\) = 101 : 216
Question 11.
Out of 1800 students in a school, 750 opted basketball, 800 opted cricket and remaining opted table tennis. If a student can opt only one game, find the ratio of
(a) Number of students who opted basketball to the number of students who opted table tennis.
(b) Number of students who opted cricket to the number of students opting basketball.
(c) Number of students who opted basketball to the total number of students.
Answer:
Total number of students = 1800
Number of students opted basketball = 750
Number of students opted cricket = 800
Therefore, number of students opted tennis = 1800 – (750 + 800) – 250
(a) Ratio of students opted basketball to that of opted table tennis
= \(\frac{750}{250}=\frac{3}{1}\) = 3 : 1
(b) Ratio of students opted cricket to students opted basketball
= \(\frac{750}{1800}=\frac{5}{12}\) = 16 : 15
(c) Ratio of students opted basketball to total no. of students
= \(\frac{750}{1800}=\frac{5}{12}\) = 5 : 12
![]()
Question 12.
Cost of a dozen pens is ₹ 180 and cost of 8 ball pens is ₹ 56. Find the ratio of the cost of a pen to the cost of a ball pen.
Answer:
Cost of a dozen pens (12 pens) = ₹ 180
∴ Cost of 1 pen = \(\frac{180}{2}\) = ₹ 15
Cost of 8 ball pens = ₹ 56
∴ Cost of 1 ball pen = \(\frac{56}{8}\) = ₹ 7
Ratio of cost of one pen to that of one ball pen = \(\frac{15}{7}\) = 15 : 7
Question 13.
Consider the statement: Ratio of breadth and length of a hall is 2 : 5. Complete the following table that shows some possible breadths and lengths of the hall.
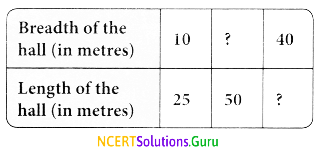
Answer:
Ratio of breadth to length = 2 : 5 = \(\frac{2}{5}\)
∴ Other equivalent ratios are
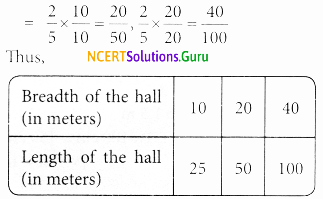
![]()
Question 14.
Divide 20 pens between Sheela and Sangeeta in the ratio of 3 : 2.
Answer:
Ratio between Sheela and Sangeeta = 3 : 2
Total these terms = 3 + 2 = 5
Therefore, the part of Sheela = \(\frac{2}{5}\) of the total pens and the part of Sangeeta = \(\frac{2}{5}\) of total pens
Thus, Sheela gets = \(\frac{3}{5}\) x 20 = 12 pens and Sangeeta gets = \(\frac{2}{5}\) x 20 = 8 pens
Question 15.
Mother wants to divide ₹ 36 between her daughters Shreya and Bhoomika in the ratio of their ages. If age of Shreya is 15 years and age of Bhoomika is 12 years, find how much Shreya and Bhoomika will get.
Answer:
Ratio of the age of Shreya to that of Bhoomika = \(\frac{15}{12}=\frac{5}{4}\) = 5 : 4
Thus, ₹ 36 divide between Shreya and Bhoomika in the ratio of 5 : 4.
Shreya gets = \(\frac{5}{9}\) of ₹ 36 = \(\frac{5}{9}\) × 36 = ₹ 20 Bhoomika gets = \(\frac{4}{9}\) of ₹ 36 = \(\frac{4}{9}\) × 36 = ₹ 16
![]()
Question 16.
Present age of father is 42 years and that of his son is 14 years. Find the ratio of
(a) Present age of father to the present age of son.
(b) Age of the father to the age of son, when son was 12 years old.
(c) Age of father after 10 years to the age of son after 10 years.
(d) Age of father to the age of son when father was 30 years old.
Answer:
(a) Ratio of father’s present age to that of son = \(\frac{42}{14}=\frac{3}{1}\) = 3 : 1
(b) When son was 12 years, i.e., 2 years ago, then father was (42 – 2) = 40
Therefore, the ratio of their ages = \(\frac{40}{12}=\frac{10}{3}\) = 10 : 3
(c) Age of father after 10 years
= 42 + 10 = 52 years
Age of son after 10 years
= 14 + 10 = 24 years
Therefore, ratio of their ages = \(\frac{52}{24}=\frac{13}{6}\) = 13 : 6
(d) When father was 30 years old, i.e., 12 years ago, then son was (14 – 12] = 2 years old
Therefore, the ratio of their ages
= \(\frac{30}{2}=\frac{15}{1}\) = 15 : 1