These NCERT Solutions for Class 10 Maths Chapter 8 Introduction to Trigonometry Ex 8.1 Questions and Answers are prepared by our highly skilled subject experts.
NCERT Solutions for Class 10 Maths Chapter 8 Introduction to Trigonometry Exercise 8.1
![]()
Question 1.
In ∆ABC right angled at B, AB = 24 cm, BC = 7 cm. Determine:
(i) sin A, cos A
(ii) sin C, cos C
Solution:
We have given that,
∆ABC is a right angle ∆, right angled at B and AB = 24 cm, BC = 7 cm
∴ By Pythagoras theorem

Question 2.
In given figure, find tan P – cot R.
Solution:
We have given that ∆PQR is a right angled A, right angle at Q. and PQ = 12 cm, PR = 13 cm
∴ By Pythagoras theorem, we know that
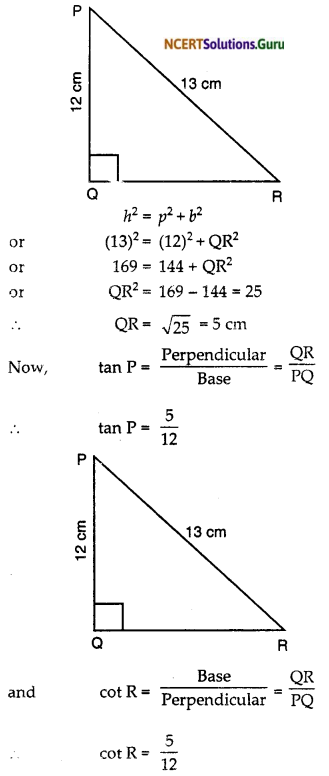
![]()
Question 3.
If sin A = \(\frac { 3 }{ 4 }\), calculate cos A and tan A.
Solution:
Given
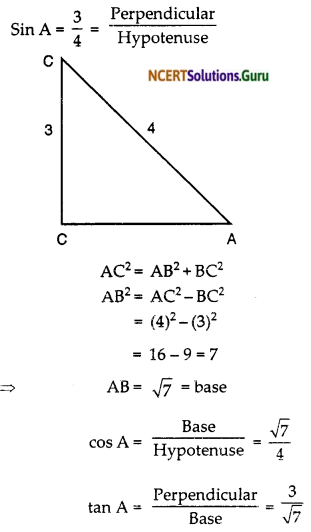
Question 4.
Given 15 cot A = 8, find sin A and sec A.
Solution:

Question 5.
Given sec θ = \(\frac { 13 }{ 12 }\) , calculate all other trigonometric ratios.
Solution:

![]()
Question 6.
If ∠A and ∠B are acute angles such that cos A = cos B, then show that ∠A = ∠B.
Solution:

Question 7.
If cot θ = \(\frac { 7 }{ 8 }\), evaluate:
(i) \(\frac { \left( 1+sin\theta \right) \left( 1-sin\theta \right) }{ \left( 1+cos\theta \right) \left( 1-cos\theta \right)}\)
(ii) cot²θ
Solution:
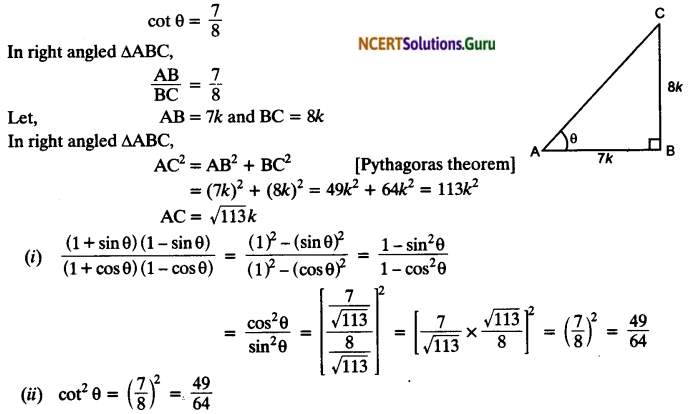
Question 8.
If 3 cot A = 4, check whether \(\frac { 1-tan^{ 2 }A }{ 1+tan^{ 2 }A }\) = cos² A – sin² A or not.
Solution:
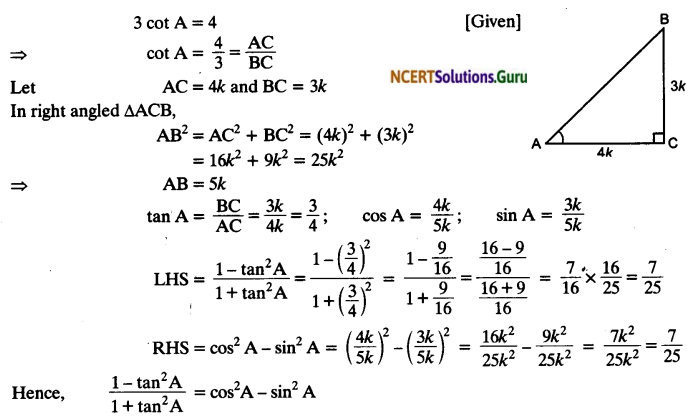
Question 9.
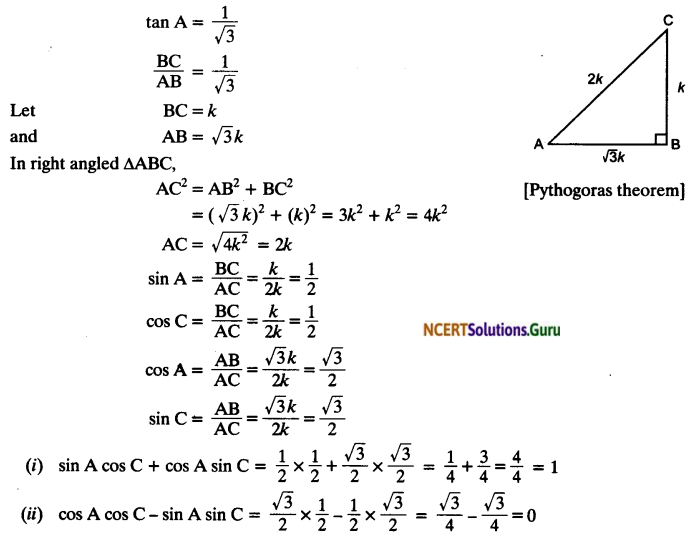
In triangle ABC, right angled at B, if tan A = \(\frac { 1 }{ \surd 3 }\), find the value of:
(i) sin A cos C + cos A sin C
(ii) cos A cos C – sin A sin C
Solution:
Question 10.
In ΔPQR, right-angled at Q, PR + QR = 25 cm and PQ = 5 cm. Determine the values of sin P, cos P and tan P.
Solution:

![]()
Question 11.
State whether the following statements are true or false. Justify your answer.
(i) The value of tan A is always less than 1.
(ii) sec A = \(\frac { 12 }{ 5 }\) for some value of angle A.
(iii) cos A is the abbreviation used for the cosecant of angle A.
(iv) cot A is the product of cot and A.
(v) sin θ = \(\frac { 4 }{ 3 }\) for some angle.
Solution:
(i) tan 60° = √3 , Since √3 > 1. (False)
(ii) sec A is always ≥ 1. (True)
(iii) cos A is the abbreviation for cosine A. (False)
(iv) cot without ∠A is meaningless. (False)
(v) sin θ can never be greater than 1.
∴ sin θ = \(\frac { P }{ H }\), hypotenuse is always greater than other two sides. (False)