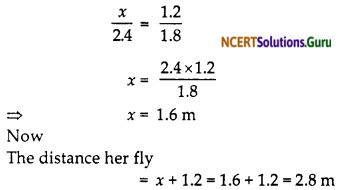These NCERT Solutions for Class 10 Maths Chapter 6 Triangles Ex 6.6 Questions and Answers are prepared by our highly skilled subject experts.
NCERT Solutions for Class 10 Maths Chapter 6 Triangles Exercise 6.6
![]()
Question 1.
In the given figure, PS is the bisector of ∠QPR of ∆PQR. Prove that \(\frac { QS }{ SR } =\frac { PQ }{ PR } \)
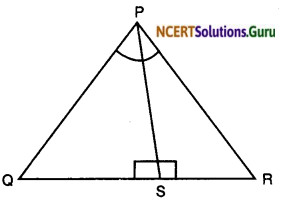
Solution:

Question 2.
In the given figure, D is a point on hypotenuse AC of ∆ABC, DM ⊥ BC and DN ⊥ AB. Prove that:
(i) DM2 = DN . MC
(ii) DN2 = DM . AN
Solution:
Given ∆ABC is right angled at B, DM ⊥ BC and DN ⊥ AB.
Construcation : Join BD.
To Prove: (i) DM² = DN. MC
(ii) DN² = DM. AN.
Proof:
(i) Consider ∆BDC
∠BDC = 90°
⇒ BDM + MDC = 90° … (i)
Also in AMCD
∠MCD + ∠MDC = 90° … (ii)
(∵ DMB = 90° by exterior theorem)
From (i) and (ii) ∠MCD = ∠BDM … (iii)
In ∆s BMD and CMD
∠CMD = ∠BMD (90° each)
∠MCD = ∠MDB (from (iii)
∴ BMD ~ DMC
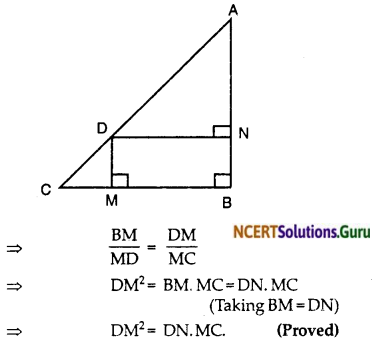
Proof (ii): Now consider similar triangles BND and AND
We
\(\frac { DN }{ DM }\) = \(\frac { AN }{ DN }\)
DN² = DM.MN (Using BN = DM)
![]()
Question 3.
In the given figure, ABc is triangle in which ∠ABC > 90° and AD ⊥ CB produced. Prove that AC2 = AB2 + BC2 + 2BC . BD
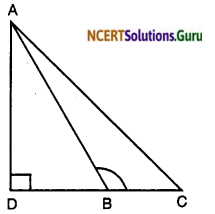
Solution:
In right angle triangle ADC. ∠D = 90°
By Pythagoras theorem.
AC² = AD² + DC²
or AC² = AD² + (BD + BC)² (DC – BD + BC)
or AC² = AD² + BD² + BC² + 2BD.BC
(a + b)² = a² + b² + 2ab)]
Now in ∆ADB ∠D produced right angle.
AB² = AD² + BD²
AD² = AB² – BD² … (ii)
From (i) and (ii)
AC² = AB² – BD² + BD² + BC² + ²BC. BD
⇒ AC² = AB² + BC² + 2BC. BD
Question 4.
In the given figure, ABC is atriangle in which ∠ABC 90° and AD ⊥ CB. Prove that AC2 = AB2 + BC2 – 2BC . BD
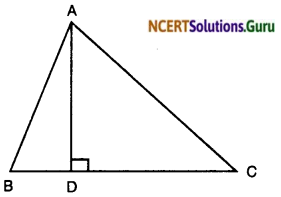
Solution:

Question 5.
In the given figure, Ad is a median of a triangle ABC and AM ⊥ BC. Prove that.
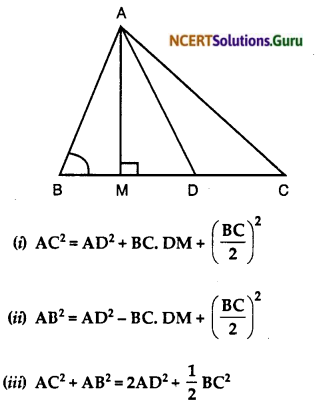
Solution:

Question 6.
Prove that the sum of the squares of the diagonals of parallelogram is equal to the sum of the squares of its sides.
Solution:
ABCD is a parallelogram and AC and BD are its diagonals.
By the property of parallelogram
∆ODC ~ ∆OAB
∆OAD ~ ∆OCB
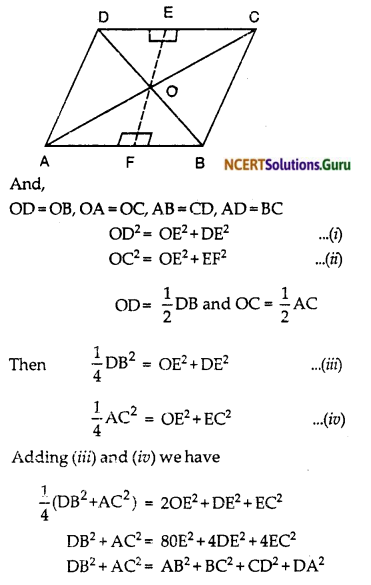
![]()
Question 7.
In the given figure, two chords AB and CD intersect each other at the point P. Prove that:
(i) ∆APC ~ ∆DPB
(ii) AP . PB = CP . DP
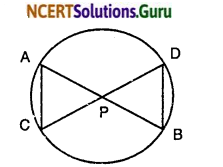
Given : Let AB and CD be the chords intersecting at P.
To Prove: (i) ∆AFC ~ ∆DPB
(ii) AP. PB = CP. DP
Proof:
(i) In ∆PAC and ∆PDB. We have
∠PAC = ∠PDB (∠s in the same segement)
∠APC = ∠BPD (Vertically opp. ∠s)
∴ ∆APC ~∆DPB (Proved)
(ii) ∆APC ~∆DPB
\(\frac { AP }{ DP }\) = \(\frac { CP }{ PB }\)
⇒ AP. PB = CP. DP (Proved)
Question 8.
In the given figure, two chords Ab and CD of a circle intersect each other at the point P (when produced) outside the circle. Prove that:
(i) ∆PAC ~ ∆PDB
(ii) PA . PB = PC . PD
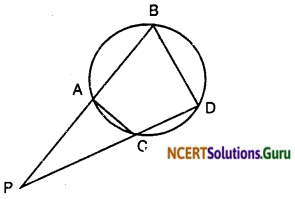
Solution:

![]()
Question 9.
In the given figure, D is a point on side BC of ∆ABC, such that \(\frac{B D}{C D}=\frac{A B}{A C}\) Prove that AD is the bisector of ∆BAC.
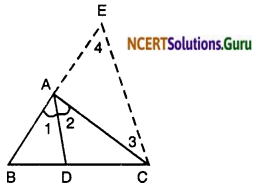
Solution:
Given: A ∆ABC, in which D is a point on BC such that
\(\frac{B D}{C D}=\frac{A B}{A C}\)
To Prove: AD is the bisector of ∠BAC.
Construction: Produce BA to E such that AE = AC. Join EC.
Proof: In ∆ACE, we have
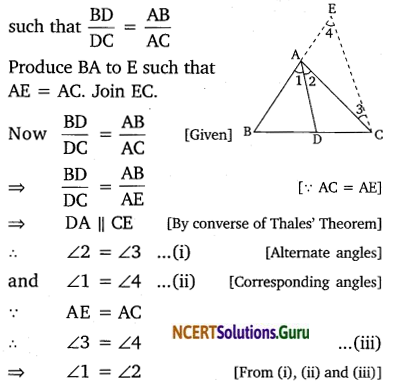
Question 10.
Nazima is fly fishing in a stream. The trip of her fishing rod is 1.8 m above the surface of the water and the fly at the end of the string rests on the water 3.6 m away and 2.4 m from a point directly under the trip of the rod. Assuming that her string (from the trip of the rod to the fly) is that, how much string does she have out (see the figure)? If she pills in the string at the rate of 5 cm per second, what will be the horizontal distance of the fly from her after 12 seconds?
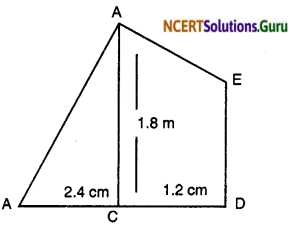
Solution:
ABC is a right triangle right angled at C by Pythagoras theorem
AB² = AC² + BC²
AB² = (1.8)² + (2.4)²
AB² = 9
AB = 3 m.
Hence 3 m the distance is
Now after the pull the vertical distance is 1.8 – 0.6 = 1.2 m
Now
∠ABC= ∠PRQ = 90°
∠B = ∠Q (The angle from water)
∆ABC ~ ∆PQR