These NCERT Solutions for Class 10 Maths Chapter 6 Triangles Ex 6.4 Questions and Answers are prepared by our highly skilled subject experts.
NCERT Solutions for Class 10 Maths Chapter 6 Triangles Exercise 6.4
![]()
Question 1.
Let ∆ABC ~ ∆DEF and their areas be, respectively, 64 cm² and 121 cm². If EF = 15.4 cm, find BC.
Solution:
Since, ∆ABC ~ ∆DEF
The ratio of the areas of two similar triangles is equal to the ratio of the squares of the corresponding sides.
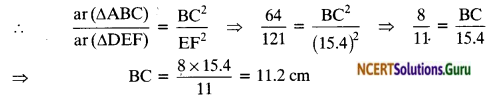
Question 2.
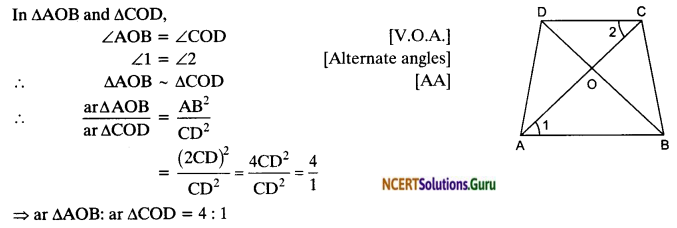
Diagonals of a trapezium ABCD with AB || DC intersect each other at the point O. If AB = 2 CD, find the ratio of the areas of triangles AOB and COD.
Solution:
ABCD is a trapezium with AB || DC and AB = 2 CD
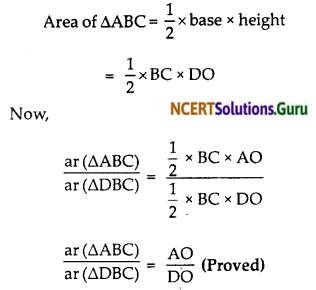
Question 3.
In the given figure, ABC and DBC are two triangles on the same base BC. If AD intersects BC at O, show that 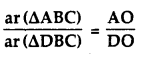
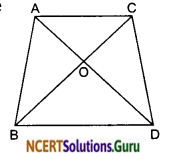
Solution:
![]()
Question 4.
If the areas of two similar triangles are equal, prove that they are congruent.
Solution:
Given : Areas of two similar triangles are equal.
To Prove : Triangles are congruent. Ratio in the areas of two similar triangles is equal to the ratio of their respective sides.
Proof: Let ∆ABC and ∆PQR be two triangles.

Hence, by SSS congruence theorem
∆ ABC ≅ ∆PQR (Proved)
Question 5.
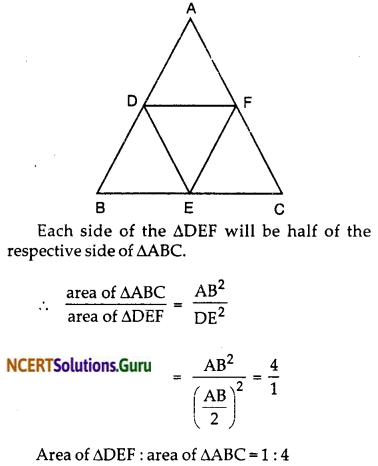
D, E and F are respectively the mid-points of sides AB, BC and CA of ∆ABC. Find the ratio of the areas of ∆DEF and ∆ABC.
Solution:
ABC is a triangle and D, E, F are the mid¬points of the sides AB, BC and CA respectively
![]()
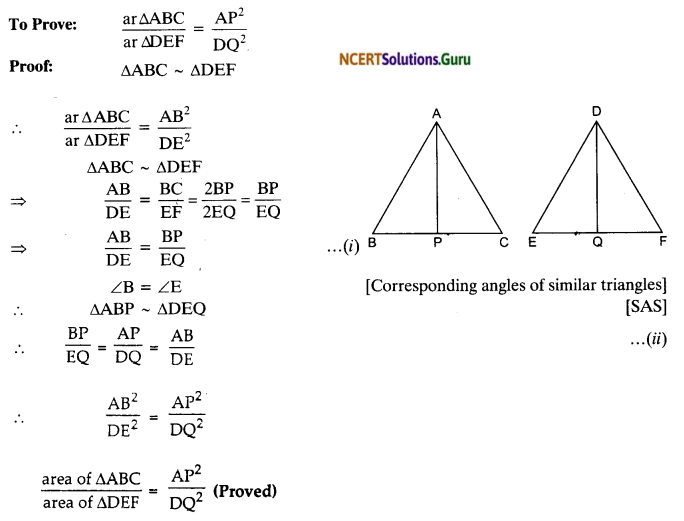
Question 6.
Prove that the ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding medians.
Solution:
Given ∆ ABC ~ ∆DEF, and AP and DQ are their medians.
![]()
Question 7.
Prove that the area of an equilateral triangle described on one side of a square is equal to half the area of the equilateral triangle described on one of its diagonals.
Solution:
Given A square ABCD. Equilateral ABCE and AACF have been described on side BC diagonal AC respectively.
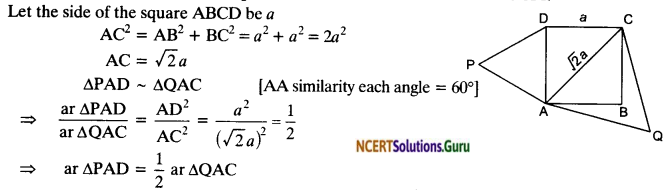
Question 8.
ABC and BDE are two equilateral triangles such that D is the mid-point of BC. Ratio of the areas of triangles ABC and BDE is _________.
(a) 2 : 1
(b) 1 : 2
(c) 4 : 1
(d) 1 : 4
Solution:
(c) 4 : 1
![]()
Question 9.
Sides of two similar triangles are in the ratio 4:9. Areas of these triangles are in the ratio __________.
(a) 2 : 3
(b) 4 : 9
(c) 81 : 16
(d) 16 : 81
Solution:
(d) 16 : 81