These NCERT Solutions for Class 9 Science Chapter 9 Force and Laws of Motion Questions and Answers are prepared by our highly skilled subject experts to help students while preparing for their exams.
Force and Laws of Motion NCERT Solutions for Class 9 Science Chapter 9
Class 9 Science Chapter 9 Force and Laws of Motion InText Questions and Answers
Question 1.
Which of the following has more inertia:
(a) a rubber ball and a stone of the same size?
(b) a bicycle and a train?
(c) a five-rupees coin and a one-rupee coin?
Answer:
Inertia is the measure of the mass of the body. The greater is the mass of the body; the greater is its inertia and vice-versa.
(a) Mass of a stone is more than the mass of a rubber ball for the same size. Hence, inertia of the stone is greater than that of a rubber ball.
(b) Mass of a train is more than the mass of a bicycle. Hence, inertia of the train is greater than that of the bicycle.
(c) Mass of a five rupee coin is more than that of a one-rupee coin. Hence, inertia of the five rupee coin is greater than that of the one-rupee coin.
An online velocity calculator of physics specifically programmed to calculate velocity/speed of a moving object.
Question 2.
In the following example, by to identify the number of times the velocity of the ball changed:
“A football player kicks a football to another player of his team who kicks the football towards the goal. The goalkeeper of the opposite team collects the football and kicks it towards a player of his own team”.
Also identify the agent supplying the force in each case.
Answer:
The velocity of the ball changes four times.
As a football player kicks the football, its speed changes from zero to a certain value. As a result, the velocity of the ball gets changed. In this case, the player applied a force to change the velocity of the ball. Another player kicks the ball towards the goal post. Asa result, the direction of the ball gets changed. Therefore, its velocity also changes. In this case, the player applied a force to change the velocity of the ball.
The goalkeeper collects the ball. In other words, the ball comes to rest. Thus, its speed reduces to zero from a certain value. The velocity of the ball has changed. In this case, the goalkeeper applied an opposite force to stop /change the velocity of the ball. The goal-keeper kicks the ball towards his team players. Hence, the speed of the ball increases from zero to a certain value. Hence, its velocity changes once again. In this case, the goalkeeper applied a force to change the velocity of the ball.
Question 3.
Explain why some of the leaves may get detached from a tree if we vigorously shake its branch.
Answer:
Some leaves of a tree get detached when we shake its branches vigorously. This is because when the branches of a tree are shaken, it moves to and fro, but its leaves tend to remain at rest. This is because the inertia of the leaves tend to resist the to and fro motion. Due to this reason, the leaves fall down from the tree when shaken vigorously.
![]()
Question 4.
Why do you fall in the forward direction when a moving bus breaks to a stop and fall backwards when it accelerates from rest?
Answer:
Due to the inertia of the passenger
Everybody tries to maintain its state of motion or state of rest. If a body is at rest, then it tries to remain at rest. If a body is moving, then it tries to remain in motion. In a moving bus, a passenger moves with the bus. As the driver applies brakes, the bus comes to rest. But, the passenger tries to maintain his state of motion.
As a result, a forward force is exerted on him. Similarly, the passenger tends to fall backwards when the bus accelerates from rest. This is because when the bus accelerates, the inertia of the passenger tends to oppose the forward motion of the bus. Hence, the passenger tends to fall backwards when the bus accelerates forward.
Question 5.
If action is always equal to the reaction, explain how a horse can pull a cart.
Answer:
A horse pushes the ground in the backward direction. According to Newton’s third law of motion, a reaction force is exerted by the Earth on the horse in the forward direction. As a result, the cart moves forward.
Question 6.
Explain, why is it difficult for a fireman to hold a hose, which ejects large amounts of water at a high velocity.
Answer:
Due to the backward reaction of the water being ejected
When a fireman holds a hose, which is ejecting large amounts of water at a high velocity, then a reaction force is exerted on him by the ejecting water in the backward direction. This is because of Newton’s third law of motion. As a result of the backward force, tire stability of the fireman decreases. Hence, it is difficult for him to remain stable while holding the hose.
Question 7.
From a rifle of mass 4 kg, a bullet of mass 50 g is fired with an initial velocity of 35 m s-1. Calculate the initial recoil velocity of the rifle.
Answer:
Mass of the rifle, m1 =4 kg
Mass of the bullet, m2 = 50g = 0.05 kg
Recoil velocity of the rifle = v1
Bullet is fired with an initial velocity, v2 = 35 m/s
Initially, the rifle is at rest.
Thus, its initial velocity, v = 0
Total initial momentum of the rifle and bullet system = (m1 + m2)v = 0
Total momentum of the rifle and bullet system after firing:
= m1v1 + m2v2 = 4(v1) + 0.05 × 35 = 4v1 + 1.75
According to the law of conservation of momentum:
Total momentum after the firing = Total momentum before the firing
4v1 + 1.75 = 0
v1 = \(\frac{1.75}{4}\) = -0.4375 m/s
The negative sign indicates that the rifle recoils backwards with a velocity of 0.4375 m/s.
![]()
Question 8.
Two objects of masses 100 g and 200 g are moving along the same line and direction with velocities of 2 ms-1 and 1 ms-1, respectively. They collide and after the collision, the first object moves at a velocity of 1.67 ms-1. Determine the velocity of the second object.
Answer:
Mass of one of the objects, m1 = 100 g = 0.1 kg
Mass of the other object, m2 = 200 g = 0.2 kg
Velocity of m1 before collision, v1 = 2 m/s
Velocity of m2 before collision, v2 = 1 m/s
Velocity of m1 after collision, v3 = 1.67 m/s
Velocity of m2 after collision = v4
According to the law of conservation of momentum:
Total momentum before collision = Total momentum after collision
∴ m1v1 + m2v2 = m1v3 + m2v4
(0.1)2 + (0.2)1.67 + (0.2)v4
0.4 + 0.167 + 0.2v4
∴ v4 = 1.165 m/s
Hence, the velocity of the second object becomes 1.165 m/s after the collision.
Class 9 Science Chapter 9 Force and Laws of Motion Textbook Questions and Answers
Question 1.
An object experiences a net zero external imbalanced force. Is it possible for the object to be travelling with a non-zero velocity? If yes, state the conditions that must be placed on the magnitude and direction of the velocity. If no, provide a reason.
Answer:
Yes. Even when an object experiences a net zero external unbalanced force, it is possible that the object is travelling with a non-zero velocity. This is possible only when the object has been moving with a constant velocity in a particular direction. Then, there is no net unbalanced force applied on the body. The object will keep moving with a non-zero velocity. To change the state of motion, a net non-zero external imbalanced force must be applied on the object.
Question 2.
When a carpet is beaten with a stick, dust comes out of it. Explain.
Answer:
Inertia of an object tends to resist any change in its state of rest or state of motion. When a carpet is beaten with a stick, then the carpet comes to motion. But, the dust particles try to resist their state of rest. According to Newton’s first law of motion, the dust particles stay in a state of rest, while the carpet moves. Hence, the dust particles come out of the carpet.
Question 3.
Why is it advised to tie any luggage kept on the roof of a bus with a rope?
Answer:
When the bus accelerates and moves forward, it acquires a state of motion. However, the luggage kept on the roof, owing to its inertia, tends to remain in its state of rest. Hence, with the forward movement of the bus, the luggage tends to remain at its original position and ultimately falls from the roof of the bus. To avoid this, it is advised to tie any luggage kept on the roof of a bus with a rope.
Question 4.
A batsman hits a cricket ball which then rolls on a level ground. After covering a short distance, the ball comes to rest. The ball slows to a stop because
(a) the batsman did not hit the ball hard enough.
(b) velocity is proportional to the force exerted on the ball.
(c) there is a force on the ball opposing the motion.
(d) there is no unbalanced force on the ball, so the ball would want to come to rest.
Answer:
(c) A batsman hits a cricket ball, which then rolls on a level ground. After covering a short distance, the ball comes to rest because there is frictional force on the ball opposing its motion.
Frictional force always acts in the direction opposite to the direction of motion. Hence, this force is responsible for stopping the cricket ball.
![]()
Question 5.
A truck starts from rest and rolls down a hill with a constant acceleration. It travels a distance of 400 m in 20 s. Find its acceleration. Find the force acting on it if its mass is 7 metric tonnes (Hint: 1 metric tonne = 1000 kg).
Answer:
Initial velocity, u = 0 (since the truck is initially at rest)
Distance travelled, s = 400 m
Time taken, t =20 s
According to the second equation of motion:
s = ut + \(\frac {1}{2}\)at2
Where,
Acceleration = a
400 = 0 + \(\frac {1}{2}\)a(20)2
400 = \(\frac {1}{2}\)a(400)
a = 2 m/s2
1 metric tonne = 1000 kg (Given)
∴ 7 metric tonnes = 7000 kg
Mass of truck, m = 7000 kg
From Newton’s second law of motion:
Force, F = Mass × Acceleration
F = ma = 7000 × 2 = 14000 N
Hence, the acceleration of the truck is 2 m/s2 and the force acting on the truck is 14000 N.
Question 6.
A stone of 1 kg is thrown with a velocity of 20 m s-1 across the frozen surface of a lake and comes to rest after travelling a distance of 50 m. What is the force of friction between the stone and the ice?
Answer:
Initial velocity of the stone, u = 20 m/s Final velocity of the stone, v = 0 (finally die stone comes to rest)
Distance covered by the stone, s = 50 m
According to the third equation of motion: v2 = u2 + 2as
Where,
Acceleration, a
(0)2 = (20)2 + 2 × a × 50
a = -4 m/s2
The negative sign indicates that acceleration is acting against the motion of the stone.
Mass of the stone, m = 1 kg
From Newton’s second law of mouon:
Force, F = Mass × Acceleration
F = ma
F = 1 × (-4) = -4 N
Hence, the force of friction between the stone and the ice is -4 N.
Question 7.
A 8000 kg engine pulls a train of 5 wagons, each of 2000 kg, along a horizontal track. If the engine exerts a force of 40000 N and the track offers a friction force of 5000 N, then calculate:
(a) the net accelerating force and
(b) the acceleration of the train.
Answer:
(a) 35000 N
(b) 1.944 m/s2
(a) Force exerted by the engine, F = 40000 N
Frictional force offered by the track, Ff = 5000
Net accelerating force, Fa = F – Ff = 40000 – 5000 = 35000 N
Hence, the net accelerating force is 35000 N.
(b) Acceleration of the train = a
The engine exerts a force of 40000 N on all the five wagons.
Net accelerating force on the wagons, Fa = 35000 N
Mass of the wagons, m = Mass of a wagon × Number of wagons
Mass of a wagon = 2000 kg
Number of wagons = 5
∴ m = 2000 × 5 = 10000kg
Total mass of the train, M = m + mass of engine = 10000 + 8000 = 18000 kg
From Newton’s second law of motion:
Fa =Ma
a = \(\frac{\mathrm{F}_{a}}{m}\)
= \(\frac{35000}{18000}\)
= 1.944 ms-2
Hence, file acceleration of the train is 1.944 m/s2.
Question 8.
An automobile vehicle has a mass of 1500 kg. What must be the force between the vehicle and road if the vehicle is to be stopped with a negative acceleration of 1.7 m s-2?
Answer:
Mass of the automobile vehicle, m = 1500 kg
Final velocity, v = 0 (finally the automobile stops)
Acceleration of the automobile, a = -1.7 ms-2
From Newton’s second law of motion:
Force = Mass × Acceleration = 1500 × (-1.7) = -2550 N
Hence, the force between tire automobile and the road is -2550 N, in the direction opposite to the motion of the automobile.
![]()
Question 9.
What is the momentum of an object of mass m, moving with a velocity v?
(a) (mv)2
(b) mv2
(c) \(\frac {1}{2}\)mv2
(d) mv
Answer:
(d) mv
Mass of the object = m
Velocity = v
Momentum = Mass × Velocity
Momentum = mv
Question 10.
Using a horizontal force of 200 N, we intend to move a wooden cabinet across a floor at a constant velocity. What is the friction force that will be exerted on the cabinet?
Answer:
A force of 200 N is applied in the forward direction. Thus, from Newton’s third law of motion, an equal amount of force will act in the opposite direction. This opposite force is the frictional force exerted on the cabinet. Hence, a frictional force of 200 N is exerted on the cabinet.
Question 11.
Two objects, each of mass 1.5 kg are moving in the same straight line but in opposite directions. The velocity of each object is 2.5 ms-1 before the collision during which they stick together. What will be the velocity of the combined object after collision?
Answer:
Mass of one of the objects, m1 = 1.5 kg
Mass of the other object, m2 = 1.5 kg
Velocity of m1, before collision, v1 = 2.5 m/s
Velocity of m2, moving in opposite direction before collision, v2 = -2.5 m/s
(Negative sign arises because mass m2 is moving in an opposite direction)
After collision, the two objects stick together.
Total mass of the combined object = m1 + m2
Velocity of the combined object = v
According to the law of conservation of momentum: .
Total momentum before collision = Total momentum after collision m1v1 + m2v2 = (m1 + m2)v
1.5(2.5) + 1.5 (-2.5) = (1.5 + 1.5)v
3.75 – 3.75 = 3 v
v = 0
Hence, the velocity of the combined object after collision is 0 m/s.
Question 12.
According to the third law of motion when we push on an object, the object pushes back on us with an equal and opposite force. If the object is a massive truck parked along the roadside, it will probably not move. A student justifies this by answering that the two opposite and equal forces cancel each other. Comment on this logic and explain why the truck does not move.
Answer:
The truck has a large mass. Therefore, the static friction between the truck and the road is also very high. To move the car, one has to apply a force more than the static friction. Therefore, when someone pushes the truck and the truck does not move, then it can be said that the applied force in one direction is cancelled out by the frictional force of equal amount acting in the opposite direction.
Therefore, the student is right in justifying that the two opposite and equal cancel each other.
Question 13.
A hockey ball of mass 200 g travelling at 10 ms-1 is struck by a hockey stick so as to return it along its original path with a velocity at 5 ms-1. Calculate the change of momentum occurred in the motion of the hockey ball by the force applied by the hockey stick.
Answer:
Mass of the hockey ball, m = 200 g = 0.2 kg
Hockey ball travels with velocity, v1 = 10 m/s
Initial momentum = mv1
Hockey ball travels in the opposite direction with velocity, v2 = -5 m/s
Final momentum = mv2
Change in momentum = mv1 – mv2 = 0.2 [10 – (-5)] = 0.2 (15) = 3 kg ms-1.
Hence, the change in momentum of the hockey ball is 3 kg m s-1.
Question 14.
A bullet of mass 10 g travelling horizontally with a velocity of 150 ms-1 strikes a stationary wooden block and comes to rest in 0.03 s. Calculate the distance of penetration of the bullet into the block. Also calculate the magnitude of the force exerted by the wooden block on the bullet.
Answer:
Now, it is given that the bullet is travelling with a velocity of 150 m/s.
Thus, when the bullet enters the block, its velocity = Initial velocity, u = 150 m/s
Final velocity, v = 0 (since the bullet finally comes to rest)
Time taken to come to rest, t = 0.03 s
According to the first equation of motion, v = u + at
Acceleration of the bullet, a
0 = 150 + (a × 0.03 s)
a = \(\frac{-150}{0.03}\) = -5000 m/s2
(Negative sign indicates that the velocity of the bullet is decreasing.)
According to the third equation of motion: v2 = u2 + 2as
0 = (150)2 + 2 (-5000) s
s = \(\frac{-(150)^{2}}{-2(5000)}=\frac{22500}{10000}\) = 2.25 m
Hence, the distance of penetration of the bullet into the block is 2.25 m.
From Newton’s second law of motion:
Force, F = Mass × Acceleration
Mass of the bullet, m = 10 g = 0.01 kg
Acceleration of the bullet, a = 5000 m/s2 .
F = ma = 0.01 × 5000 = 50 N
Hence, the magnitude of force exerted by the wooden block on the bullet is 50 N.
![]()
Question 15.
An object of mass 1 kg travelling in a straight line with a velocity of 10 ms-1 collides with, and sticks to, a stationary wooden block of mass 5 kg. Then they both move off together in the same straight line. Calculate the total momentum just before the impact and just after the impact. Also, calculate the velocity of the combined object.
Answer:
Mass of the object, m1 = 1 kg
Velocity of the object before collision, v1 = 10 m/s
Mass of the stationary wooden block, m2 = 5
Velocity of the wooden block before collision, v2 = 0 m/s
∴ Total momentum before collision = m1v1 + m2v2
= 1 (10) + 5 (0) = 10 kg ms-1
It is given that after collision, the object and the wooden block stick together.
Total mass of the combined system = m1 + m2
Velocity of the combined object = v
According to the law of conservation of momentum:
Total momentum before collision = Total momentum after collision
m1v1 + m2v2 = (m1 + m2)v
1 (10) + 5 (0) = (1 + 5)u
v = \(\frac{10}{6}=\frac{5}{3}\) m/s
The total momentum after collision is also 10 kg m/s.
Total momentum just before the impact = 10 kg ms-1
Total momentum just after the impact = (m1 + m2)v = 6 × \(\frac{5}{3}\) = 10 kg ms-1
Hence, velocity of the combined object after collision = \(\frac{3}{5}\) m/s
Question 16.
An object of mass 100 kg is accelerated uniformly from a velocity of 5 m s-1 to 8 ms-1 in 6 s. Calculate the initial and final momentum of the object. Also, find the magnitude of the force exerted on the object.
Answer:
Initial velocity of the object, u = 5 m/s
Final velocity of the object, v = 8 m/s
Mass of the object, m = 100 kg
Time take by the object to accelerate, t = 6s
Initial momentum = mu = 100 × 5 = 500 kg ms-1
Final momentum = mv = 100 × 8 = 800 kg ms-1
Force exerted on the object, F = \(\frac{m v-m u}{t}\)
\(=\frac{m(v-u)}{t}=\frac{800-500}{6}=\frac{300}{6}\) = 50 N
Initial momentum of the object is 500 kg ms-1.
Final momentum of the object is 800 kg ms-1.
Force exerted on the object is 50 N.
Question 17.
Akhtar, Kiran and Rahul were riding in a motor car that was moving with a high velocity on an expressway when an insect hit the windshield and got stuck on the windscreen. Akhtar and Kiran started pondering over the situation. Kiran suggested that the insect suffered a greater change in momentum as compared to the change in momentum of the motorcar (because the change in the velocity of the insect was much more than that of the motorcar). Akhtar said that since the motorcar was moving with a larger velocity, it exerted a larger force on the insect. And as a result the insect died. Rahul while putting an entirely new explanation said that both the motorcar and the insect experienced the same force and a change in their momentum. Comment on these suggestions.
Answer:
According to the law of conservation of momentum:
Momentum of the car and insect system before collision = Momentum of the car and insect system after collision
Hence, the change in momentum of the car and insect system is zero.
The insect gets stuck on the windscreen. This means that the direction of the insect is reversed. As a result, the velocity of the insect changes to a great amount. On the other hand, the car continues moving with a constant velocity. Hence, Kiran’s suggestion that the insect suffers a greater change in momentum as compared to the car is correct. The momentum of the insect after collision becomes very high because the car is moving at a high speed. Therefore, the momentum gained by the insect is equal to the momentum lost by the car.
Akhtar made a correct conclusion because the mass of the car is very large as compared to the mass of the insect.
Rahul gave a correct explanation as both the car and the insect experienced equal forces caused by the Newton’s action-reaction law. But, he made an incorrect statement as the system suffers a change in momentum because the momentum before the collision is equal to the momentum after the collision.
Question 18.
How much momentum will a dumbbell of mass 10 kg transfer to the floor if it falls from a height of 80 cm? Take its downward acceleration to be 10 ms-2.
Answer:
Mass of the dumbbell, m = 10 kg
Distance covered by the dumbbell, s = 80 cm = 0.8 m
Acceleration in the downward direction, a = 10 m/s2
Initial velocity of the dumbbell, u = 0
Final velocity of the dumbbell (when it was about to hit the floor) = v
According to the third equation of motion: v2 = u2 + 2as
v2 = 0 + 2 (10) 0.8
v = 4 m/s
Hence, the momentum with which the dumb-bell hits the floor is
= mv = 10 × 4 = 40 kg ms-1
Question 19.
The following is the distance-time table of an object in motion:
| Time in seconds | Distance in metres |
| 0 | 0 |
| 1 | 1 |
| 2 | 8 |
| 3 | 27 |
| 4 | 64 |
| 5 | 125 |
| 6 | 216 |
| 7 | 343 |
(a) What conclusion can you draw about the acceleration? Is it constant, increasing, decreasing, or zero?
(b) What do you infer about the forces acting on the object?
Answer:
(a) There is an unequal change of distance in an equal interval of time.
Thus, the given object is having a non-uniform motion. Since the velocity of the object increases with time, the acceleration is increasing.
(b) According to Newton’s second law of motion, the force acting on an object is directly proportional to the acceleration produced in the object. In the given case, the increasing acceleration of the given object indicates that the force acting on the object is also increasing.
![]()
Question 20.
Two persons manage to push a motorcar of mass 1200kg at a uniform velocity along a level road. The same motorcar can be pushed by three persons to produce an acceleration of 0. 2 ms-2. With what force does each person push the motorcar? (Assume that all persons push the motorcar with the same muscular effort)
Answer:
Mass of the motor car = 1200 kg Only two persons manage to push the car. Hence, the acceleration acquired by the car is given by the third person alone.
Acceleration produced by the car, when it is pushed by the third person, a = 0.2 m/s2
Let the force applied by the third person be F. From Newton’s second law of motion:
Force = Mass × Acceleration
F = 1200 × 0.2 =240 N
Thus, the third person applies a force of magnitude 240 N.
Hence, each person applies a force of 240 N to push the motor car.
Question 21.
A hammer of mass 500 g, moving at 50 ms-1, strikes a nail. The nail stops the hammer in a very short time of 0.01 s. What is the force of the nail on the hammer?
Answer:
Mass of the hammer, m=500 g = 0.5 kg
Initial velocity of the hammer, u = 50 m/s
Time taken by the nail to the stop the hammer, t = 0.01 s
Velocity of the hammer, v = 0 (since the hammer finally comes to rest)
From Newton’s second law of motion:
Force, F= \(\frac{m(v-u)}{t}=\frac{0.5(0-50)}{0.01}\) = -2500N
The hammer strikes the nail with a force of -2500 N. Hence, from Newton’s third law of motion, the force of the nail on the hammer is equal and opposite, i.e., +2500 N.
Question 22.
A motorcar of mass 1200kg is moving along a straight line with a uniform velocity of 90 km/h. Its velocity is slowed down to 18 km/h in 4 s by an unbalanced external force. Calculate the acceleration and change in momentum. Also calculate the magnitude of the force required.
Answer:
Mass of the motor car, m = 1200 kg
Initial velocity of the motor car, u = 90 km/h = 25 m/s
Final velocity of the motor car, v = 18 km/h = 5 m/s
Time taken, t = 4 s
According to the first equation of motion:
v = u + at
5 = 25 + a (4)
a = – 5 m/s2
Change in momentum = mv – mu = m (v – u)
= 1200 (5 – 25) = -24000 kg ms-1
Force = Mass × Acceleration
= 1200 × (-5) = -6000 N
Acceleration of the motor car = -5 m/s2
Change in momentum of the motor car = -24000 kg ms-1
Hence, the force required to decrease the velocity is -6000 N.
(Negative sign indicates the retardation, decrease in momentum and retarding force respectively)
Class 9 Science Chapter 9 Force and Laws of Motion Additional Important Questions and Answers
Multiple Choice Questions
Choose the correct option:
Question 1.
Which of the following statement is not correct for an object moving along a straight path in an accelerated motion?
(a) Its speed keeps changing
(b) Its velocity always changes
(c) It always goes away from the earth
(d) A force is always acting on it
Answer:
(c) It always goes away from the earth
Question 2.
According to the third law of motion, action and reaction
(a) always act on the same body
(b) always act on different bodies in opposite directions
(c) have same magnitude and directions
(d) act on either body at normal to each other
Answer:
(b) always act on different bodies in opposite directions
Question 3.
A goalkeeper in a game of football pulls his hands backwards after holding the ball shot at the goal. This enables the goal keeper to
(a) exert larger force on the ball
(b) reduce the force exerted by the ball on hands
(c) increase the rate of change of momentum
(d) decrease the rate of change of momentum
Answer:
(b) reduce the force exerted by the ball on hands
Question 4.
The inertia of an object tends to cause the object
(a) to increase its speed
(b) to decrease its speed .
(c) to resist any change in its state of motion
(d) to decelerate due to friction
Answer:
(c) to resist any change in its state of motion
![]()
Question 5.
A passenger in a moving train tosses a coin which falls behind him. It means that motion of the train is
(a) accelerated
(b) uniform
(c) retarded
(d) along circular tracks
Answer:
(a) accelerated
Question 6.
An object of mass 2 kg is sliding with a constant velocity of 4 ms-1 on a frictionless horizontal table. The force required to keep the object moving with the same velocity is
(a) 32 N
(b) 0 N
(c) 2 N
(d) 8N
Answer:
(b) 0 N
Question 7.
Rocket works on the principle of conservation of
(a) mass
(b) energy
(c) momentum
(d) velocity
Answer:
(c) momentum
Question 8.
A water tanker filled up to 2/3 of its height is moving with a uniform speed. On sudden application of the brake, the water in the tank would
(a) move backward
(b) move forward
(c) be unaffected
(d) rise upwards
Answer:
(b) move forward
Question 9.
Which of the following is the measure of inertia?
(a) Volume
(b) Velocity
(c) Momentum
(d) Mass
Answer:
(d) Mass
![]()
Question 10.
The S.I. unit of momentum is
(a) ms-1
(b) ms-2
(c) kg ms-2
(d) kg ms-1
Answer:
(d) kg ms-1
Very Short Answer Type Questions
Question 1.
Define force.
Answer:
Force is defined as a pull or push that changes the position or shape or state of a body.
Question 2.
Define inertia.
Answer:
Inertia is the natural tendency of a body to stay at rest or to remain in motion with same velocity.
Question 3.
State the S.I. unit of inertia.
Answer:
Mass is the measure of inertia therefore S.I. unit of inertia is kilogram (kg).
Question 4.
What will be the acceleration of a body which is moving under the balanced force.
Answer:
If a body moves under the balanced force than its acceleration is zero.
Question 5.
Why a groove is povided in a saucer?
Answer:
A groove is provided in a saucer to prevent the toppling of cup due to a sudden jerk.
Question 6.
Why does a fan continue to move for sometime even after if has been switched off?
Answer:
When a fan is switched off, it tends to remain in motion due to inertia it gained during its motion.
![]()
Question 7.
Which of the two, a truck or trains has greater inertia? Why?
Answer:
A train has greater inertia because of its greater mass.
Question 8.
Define the SlI. unit of force.
Answer:
S.I. unit of force, Newton (N) is defined as force that produces an acceleration of 1 m/s2 in a body of mass 1 kg.
Question 9.
How does the acceleration of a body changes on application of unbalanced force?
Answer:
The acceleration produced in a body is directly proportional to the applied unbalanced force.
Question 10.
According to third law of motion, action and reaction acts on same or different bodies?
Answer:
Action and reaction always act on two different bodies.
Question 11.
Give two examples in which force is applied from a distance.
Answer:
Non-contact forces include magnetic force and gravitational force.
Question 12.
What is the total momentum of the gun and bullet before firing of the bullet?
Answer:
With both gun and bullet in rest, the total momentum before firing of bullet is zero.
Question 13.
Which law of motion is also considered as the law of inertia?
Answer:
First law of motion is also considered as the law of inertia.
![]()
Question 14.
What is force of friction?
Answer:
Force of friction is defined as the force that acts against the direction of motion of body to oppose the motion.
Question 15.
What are the S.I unit of momentum and force?
Answer:
S.I. unit of momentum is kg ms~J and of force is kg ms-2 (Newton).
Short Answer Type Questions
Question 1.
What are balanced and unbalanced forces?
Answer:
Balanced forces : When two or more forces act on a body and their resultant force is zero which do not change the state of rest or motion of a body, the forces are called balanced forces.
Example : When a wooden block is pulled from both sides with equal but opposite forces, the wooden block does not undergo any displacement, it remains at its original position.
Unbalanced forces: When the resultant of two or more forces acting on a body is not zero hence, bring the change in the position, state or shape of body, the forces are called imbalanced forces.
Example: Kicking of a football by player or with drawing of water from a well.
Question 2.
State the different possible effects of the ‘ application of force on an object.
Answer:
The different possible effects of the application of force on an object include:
(i) Displacement of object from its initial po-sition.
(ii) Change in the direction of motion of a body.
(iii) Change in the shape of a body.
(iv) Change in the state of a body.
Question 3.
Give reasons for the following:
(i) A foot ball when kicked flies away but not a solid metallic ball of same size.
(ii) A rubber ball covers a longer distance than a leather ball thrown with same force.
(iii) You travelling in car happened to be pushed to one side, when the car takes a sharp turn.
(iv) A passenger moving from a running bus ends up fall with his face downward.
(v) Driver and passengers of a car are advised to wear safety belts.
Answer:
(i) The mass of metallic ball is more than the foot ball hence, metallic ball has greater inertia than fooball. It has lesser tendency to bring change in its position.
(ii) A rubber ball has less mass and we know that acceleration is inversely proportional to mass, therefore rubber ball gains more acceleration and covers large distance than heavier leather ball on application of equal force.
(iii) When travelling in a car, the direction of motion of body is in the direction of the motion of car but when the car suddenly takes a sharp turn the direction of car changes but not of the passenger. Therefore, he is pushed to one side of the car.
(iv) When a passenger jumps out from a moving bus, his feet comes in state of rest on touching the ground but his upper body tends to remain in the state of motion due to inertia. Therefore, the passenger tends to fall with his face downward.
(v) The body of the driver and passenger in a moving car tends to be in the state of motion.
Therefore, to stop the body going forward on the application of sudden brakes, they are adviced to wear seat belt. The seat belts also called safety belts. Exerts a force on passengers body to make forward motion, due to inertia, much slower.
![]()
Question 4.
A student placed a water filled tumbler on a tray and turned around as fast as he could? What do you expect to happen to the tumbler? Why?
Answer:
The tumbler would topple down spilling the water.
Initially both tumbler and tray were in state of rest but as student after turning around came to stand still the tray came in rest but not the tumbler, it remained in motion because of inertia and therefore fell down, spilling the water.
Question 5.
Why does a sprinter keep running for sometime even after crossing the finish line?
Answer:
A sprinter keeps running for sometime to some distance even after crossing the finish line because of inertia that opposes the change in state of motion of his body.
Question 6.
What do you mean by momentum ? What is its S.I. unit?
Answer:
Momentum refers to the product of mass with die velocity of a body in motion. It’s a vector quantity which has both the magnitude and direction. The direction is same as the direction of the velocity.
Momentum = mass × velocity
or P = m × v
It’s S.I. unit is kg ms-1 (kilogram meter per second).
Question 7.
State the three laws of motion.
Answer:
First law of motion : It states that an object at rest or in uniform motion will remain in rest or uniform motion unless unbalanced force acts on it.
Second law of motion: It states that the rate of change of momentum of an object is proportional to the applied force and always takes place in the direction of the force.
If P1 and p2 are the change in momentum in time ‘t’ an object of mass ‘m’, then

Third law of motion: It states that when an object exert a force on another object, then the second object exerts the force on the first object. These two forces are always equal in magnitude but in the opposite direction i.e. action and reaction forces are always equal in magnitude but opposite in the direction.
Question 8.
Deduce the first law of motion from second law of motion.
Answer:
When F is the applied force on a body of mass ‘m’ then if body gains acceleration ‘a’ then according to 2nd law of motion.
F = ma
F = m \(\frac{(v-u)}{t}\left(a=\frac{v-u}{t}\right)\)
or Ft = m(v – u) or mv – mu
When F = 0 with body at rest
mv – mu = 0
mv = mu
or v = u
This shows that the object would continue to move with same uniform velocity ‘u’ through the timer.
![]()
Question 9.
How does the acceleration of an object changes with the
(a) applied unbalanced force?
(b) mass of the object?
Answer:
(a) Acceleration of an object is directly proportional to the unbalanced force applied on the object. It increases with the increasing force.
(b) Acceleration of an object is inversely proportional to the mass of the object. Acceleration of an object decreases with increasing mass keeping the applied imbalanced force constant.
Question 10.
Explain why a Karate player breaks a slab of ice or brick or a pile of tiles by striking with his hand in a single blow?
Answer:
A Karate player strikes the slab of ice or a pile of tiles as fast as possible with his hand. In doing so, the entire momentum of the hand is reduced to zero in a short time. This causes the application of large force on pile of tiles or slab of ice to break.
Question 11.
Explain why a fielder in the ground moves his hand backward while catching a moving cricket ball?
Answer:
The fielder in the ground gradually pulls his hand backward when catching the ball so that ball is stopped in longer time. This allows the acceleration of ball to reduce gradually causing less impact on hand/palm to protect them from getting hurt.
Question 12.
Explain why in a high jumping ground, the athletes are made to fall either on a cushioned bed or on a sand bed?
Answer:
When an athlete after making a jump, falls on a cushioned bed or on a sand bed, the time of athletes’ fall after making a jump increases hence, reduces the rate of change of momentum and force to cause less impact on athlete.
Question 13.
Action and reaction force are equal in the magnitude, do they produce equal acceleration in the two bodies? Why?
Answer:
Action and reaction forces are equal in their magnitude but they may or may not produce equal acceleration in the two bodies because acceleration produced is inversely proportional to mass. The body with less mass will experience greater acceleration than body with greater mass.
![]()
Question 14.
Explain how you manage to walk easily on road but end up slipping if happened to step on the banana peel?
Answer:
When we walk on the ground, we push the road or ground below backwardly with a force. This force is the action. Then, in turn we get a reaction of the applied force which is equal in magnitude but opposite in direction to enable us to move forward.
When we happen to step on banana peel, the force of friction is very-very less and hence, we end up slipping.
Question 15.
Explain the principle of the working of jet engine.
Answer:
In a jet engine a large volume of the gases are produced by burning of fuel. These gases are allowed to escape throuh a jet or nozzle at the rear end of jet-engine at a very high speed in the backward direction forcing the body to go in forward direction with high velocity.
Question 16.
What do you mean by interaction? State the different types of interactions.
Answer:
When an object influences another object by the application of force, the first object is said to be interacted with second object.
The interaction may happen when two bodies come in direct contact of each other such as the muscular force applied by a person on an object or from a distance such as magnetic or electrical force. A magnet or an electrical charge exerts its force from a distance Le. without coming in contact of another object.
Question 17.
Where do you find easy to walk, on a sandy or tar road?
Answer:
It is easier to walk on a tar road than on a sandy road. When we step over a patch of sand, the sand particles get displaced by the foot take sometime to reach the sandy ground. Therefore the action from the sandy soil is reduced and so also the reaction in the feet. This reduced action and reaction makes it difficult to walk on sandy road than on tar road.
Question 18.
A student hits a floor and mattress lying on the same floor. In which case, he will hurt himself more? Why?
Answer:
When the student hits the cemented floor and a mattress lying on the floor, then he will feel more hurt on hitting the floor than mattress. The mattress being soft increases the impact time but decreases the rate of change of momentum.
Question 19.
A constant force acts on an object of 5 kg mass for a period of 2 s. It increases its velocity from 3 ms-1 to 7 ms-1. Find the magnitude of the applied force. If the force is applied for 4 seconds, what could be the final velocity?
Answer:
Mass of object = 5 Kg
Initial velocity (u) =3 ms-1
Time taken for applied force = 2s
We know that F = \(\frac{m(v-u)}{t}=\frac{5(7-3)}{2}=\frac{5 \times 4}{2}\) = 10 N
If the force is appled for, 4 seconds, then Initial velocity, u = 3ms-1, F = 10 N, v = 7
F = \(m \frac{(v-u)}{t}\)
10 = \(5 \frac{(v-3)}{4}\)
\(\frac {40}{5}\) = v – 3
v = 8 + 3
v = 11 ms-1
![]()
Question 20.
Which would require a greater force accelerating a 2 kg mass at 5 ms-2 or a 4 kg mass at 2 ms-2?
Answer:
(i) Mass of the object = 2 kg
Acceleration, a = 5 ms-2
Force = Mass × Acceleration = 2 × 5 = 10N
(ii) Mass of the object = 4 kg
Acceleration, a = 2 ms-2
Force = Mass × Acceleration = 4 × 2 = 8N
Therefore, accelerating 2 kg mass would require more force.
Question 21.
A motor car is moving with a velocity of 108 Km/h and it takes 4 s to stop after the brakes are applied. Calculate the force exerted by the brakes on the motor car if its mass along with the passengers in motor car is 1000 kg.
Answer:
Initial velocity of car (u) = 108 km/h.
= \(\frac{108 \times 1000}{3600}\) = 30 ms-1
Final velocity = 0 ms-1
Time taken = 4 s
Mass of motor car = 1000 kg
∴ Magnitude of force applied, F = \(m \frac{(v-u)}{t}\)
= \(1000 \frac{(0-30)}{4}\)
= – 7500 N
The negative sign indicates that the force is acting in the direction opposite to the direction of motion of motor car.
Question 22.
A force of 5N gives an acceleration of 120 ms-2 in mass m2. What acceleration would it give if both the masses m, and m2 are tied together?
Answer:
(i) Force F = 5N
Acceleration, a = 10 ms-2
mass, m = ?
with F = m × a
5 = m × 10
or, m = \(\frac {5}{10}\) = 0.5 kg
(ii) Force, F = 5N
Acceleration, a =20 ms-2
With F = m × a
5 = m × 20
m = \(\frac {5}{20}\)
= \(\frac {1}{4}\)
= 0.25 kg
When masses are tied together = 0.5 + 0.25 kg
= 0.75 kg.
Withforce F =5N
and mass m =0.75 kg
a = \(\frac{F}{m}=\frac{5}{0.75}\)
= 6.67 ms-2
Question 23.
The velocity-time graph of a ball of mass 20 g moving along a straight line on a long table 15 shown in the figure 9.1 given below.
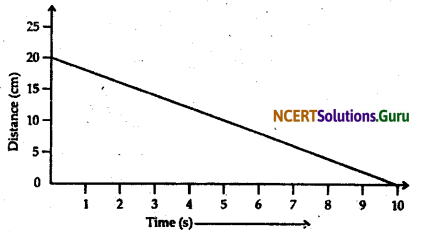
How much force does the table exert on the ball to bring it to rest?
Answer:
Initial velocity of ball (u) = 20cm-1 = 0.2ms-1
Final velocity of ball, (v) = 0
Time taken (t) = 10s
Mass of ball = 20g = 0.02kg

= -0.0004 N
The negative sign show that force is acting against the direction of motion.
![]()
Question 24.
What would be the force required to produce acceleration of 2ms-2 on a body of mass 12 kg? What would be its acceleration, if the force applied is doubled to its initial value?
Answer:
Acceleration, a = 2ms-2
mass, m = 12kg
∴ Force required = Mass × Acceleration
= 12 × 2 = 24 N
When force is doubled, than F = 24 × 2 = 48 N
Mass of body = 12 kg
∴ Acceleration = \(\frac{\text { Force }}{\text { mass }}=\frac{48}{12}\) = 4 ms-2
Question 25.
A man pushes a box of 50 kg with a force of SON. What will be the acceleration of the box due to this force? If the mass of the box was halved what would be the acceleration?
Answer:
Mass of the box, m = 50 kg
Force applied, F = 80 N
Then acceleration, a = \(\frac{\mathrm{F}}{\mathrm{M}}\)
= \(\frac {80}{50}\) = 1.6 ms-2
When the mass is healed = \(\frac {50}{2}\)
= 25kg.
Force applied = 80 N
Then acceleration, a = \(\frac{\mathrm{F}}{\mathrm{M}}\)
= \(\frac {80}{25}\) = 3.2ms-2
Question 26.
A force exerted for 1.2s raises the velocity of an object from 1.8 ms-1 to 4.2 ms-1. If mass of object is 5.5 kg, calculate the force applied on the object?
Answer:
Initial velocity, u = 1.8ms-1
Time taken, t = 1.2s
Final velocity, v = 4.2 ms-1
Mas of the object = 5.5kg
Force applied, F = \(m \frac{(v-u)}{t}\)
= \(5.5 \frac{(4.2-1.8)}{1.2}=\frac{5.5 \times 2.4}{1.2}\) = 11 N
Question 27.
A bullet of mass 20 kg is horizontally fired from a pistol of mass 2kg with a horizontal velocity of 150 ms-1. What is the recoil velocity of the pistol?
Answer:
Mass of bullet =20g = 0.02kg
Mass of pistol = 2kg
Before firing, momentum = 0
Therefore u1 =1
and u2 =0
Final velocity of bullet = 150ms-1
Final velocity of pistol = v
Total momentum of pistol and bullet after firing = m1v1 + m2v2
Initial and final momentum are equal therefore
3.0 + 2v = 0
v = \(\frac {-3}{2}\)1.5ms-1
The negative sign shows that the direction of the motion of bullet and pistol are in opposite direction.
Question 28.
A girl of mass 40 kg jumps with a horizontal velocity of 5ms-1 into a stationary cart with frictionless wheels. The mass of cart is 3kg. What is her velocity when she moves off the cart?
Answer:
Mass of- girl, m1 =40kg
Mass of cart, m2 = 3kg
Initial velocity, u1 = 5 ms-1
Initial velocity, u2 = 0 ms-1
The momentum of the girl and cart before interaction
= 40 × 5 + 3 × 0
= 200 kg ms-1
After interaction, velocity of cart + girl = v.
Total momentum after interaction = (m1, + m2) v.
= (40 + 3) v = 43v
Total momentum before interaction = Total momentum after interaction.
430v = 200
v = 4.65 ms-1
![]()
Question 29.
Two hockey players of opposite teams, while trying to hit a hockey ball in the ground colloid and immediately become entangled. One has mass of 80 kg and moving with a velocity of 5 0 ms-1. While the other has mass of 70 kg and is moving with a velocity of 6 ms-1 towards the first player. In which direction and with what velocity they will move after they combine together? Assume that the friction force acting between the ground and feet of two players is negligible.
Answer:
Mass of Is hockey player = 80kg
It’s initial velocity u = 5 ms-1
Mass of 2nd hockey player = 70 kg
Initial velocity of 2nd player u2 = – 6 ms-1
Therefore total momentum before collision = m1 + u2 + m2u2
= 80 × 5 + 70 × (-6)
= 400 – 420 = -20 kg ms-1
Let velocity of two entangled players after collision = v
Total momentum = (m1 + m2)v = (80 + 70) v = 150M.
According to law of conservation of momentum. Momentum before collosion Momentum after collision
1500 = -20
v = \(\frac {-20}{150}\) = 0.13 ms-1
The entangled players will move indirection of the second player.
Question 30.
A motor car of mass 800 kg was moving with a uniform velocity of 60 km/h along a straight line when the driver applied the brakes after seeing a child crossing road to reduce its speed to half of its original speed. Calculate the change in momentum and force applied by the driver in brakes in 2 s.
Answer:
Mass of car =800 kg
Initial velocity, u = 60 km/h = 16.6 m/s
Final velocity of car v = 30.km/h = 8.3 m/s
Time taken =2s
so Acceleration = \(\frac{v-u}{t}=\frac{16.6-8.3}{2}\)
= \(\frac {6.3}{2}\) = 3.15 ms-2
Change in momentum = mv – mu = m(v – u)
= 800 (16.6 – 8.3) = 6640 kg ms-1
Force required, F = m × a = 800 × 3.15
= 2520N.
Long Answer Type Questions
Question 1.
Describe an experiment on the basis of which Galileo suggested that objects move with constant speed when no force acts on them.
Answer:
Galileo observed the motion of objects on inclined plane. He observed that when a marble rolls down an inclined plane, its velocity increases due to the unbalanced force of gravity. It attains a definite velocity tire time it reaches the bottom. It’s velocity decreases when it climbs upon an inclined plane as shown in the fig. 9.2. He further noted that on a frictionless plane inclined equally on both side, when a marble is released from one side it would roll down the slope and climb up to the opposite side to the same height from which it was released.
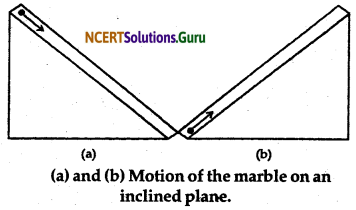
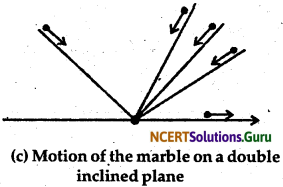
If the angle of inclination on one side is gradually decresed then marble would have to cover a large distance to reach the same height as shown in the fig. (c). If the one side of the plane ultimately is made horizontal (or slope is reduced to zero), the marble would continue to travel forever to reach the same height it was released. These imbalanced forces acting on the marble in this case is zero. I suggests that no imbalanced force is required to keep the marble moving with constant velocity. However, in practical situation, it is difficult to achieve a zero unbalanced force. This is because of the presence of friction for acting in opposite to the direction of motion. Thus, in practice marble stops after tavelling some distance. The effect of friction must be reduced by using smoother marble and smoother plane and providing a lubricant.
![]()
Question 2.
State and explain the first law of motion.
Answer:
First law of motion: According to the first law of motion body or an object at rest or in a uniform motion will remain at rest or in uniform motion unless an unbalanced force acts upon it.
Explanation: This law consists of two parts.
(i) A body at rest remains at rest unless a force is applied on it: A book lying on a table or a box lying on a floor remain at rest until someone tries to disturb it which means it will remain in its respective position of rest unless imbalanced force acts upon them.
(ii) The object in uniform motion will continue moving in straight line with same uniform motion unless unbalanced external force acts on it. This part seems to be contrary in our daily life experiences. Usually, we observe that the moving object slow down and come to rest after sometime. It occurs due to the force of friction that opposes the motion of the object.
The ball is released from a certain height on an inclined plane placed on a horizontal plane. Note the distance moved by the ball before it stops. Roll the same ball from the same height on inclined plane placed on a glass sheet and note the distance travelled by the ball before it stops. We will find that the distance covered by ball glass sheet will be longer than the rough surface. This shows that if the resistance of the air and friction force offered by the surface is reduced the ball on will cover more and more distance. If the surface becomes completely frictionless and their is no resistance of air the ball will continue moving with uniform motion in a straight line.
Question 3.
What is the intertia of rest? Demonstrate it with the help of an activity.
Or
How will you demonstrate that an object will remain at rest unless acted upon by an unbalanced force?
Answer:
Intertia of rest: A body always tends to remain in the position of rest or tendency of body to resist any change in its state of rest is known as inertia of rest. It can be demonstrated by the following activities.
Activity 1 : Take an empty glass tumbler and place a thick or stiff playing card on the top of the empty glass tumbler. Place a five rupees coin on the card as shown in the fig 9.3. Give the card a horizontal flick with a finger. The card shoots away allowing the coin to fall vertically into the glass tumbler due to its inertia of rest. The inertia keeps the coin to maintain its state of rest even when the card flow off.

Activity 2 : Make a pile of similar carom coin on a table as shown in the fig. 9.4. Now give a horizontal hit at the bottom of the pile using a striker. If the hit is strong enough then the bottom coins moves quickly and are removed from their place but the rest of the pile will not move horizontally but they fall vertical on the floor due to the inertia of the other coins.

Question 4.
Derive the relation “F = ma” by using Newtons second law of motion. How will you define the S.I. unit of force from this law?
Answer:
According to the second law of motion, the rate of change of momentum of a body is directly proportional to the imbalanced force applied on the body and always takes place in the direction of the force.
Let a body of mass ‘m’ is moving with an initial velocity along a straight line. It is uniformly accelerated to velocity V in the time T by the application of constant force F through the time t.
The initial momentum of the body = mu
Final momentum of the body = mv
Change of momentum ∝ mv – mu
∝ m (v – u)
Change in momentum per unit time = \(\frac{m(v-u)}{t}\)
But change in momentum per unit time = Applied force.
Therefore F ∝ \(\frac{m(v-u)}{t}\)
But \(\frac{(v-u)}{t}\) = a = acceleration produced produced in the body
F ∝ m.a.
F = k.m.a. (where k is constant of proportionality).
One unit of force is defined as the amount that produces an acceleation of 1m/s2 in an object of mass 1 kg i.e.
1 (unit of force) = k. (1 kg) × 1 (ms-2)
k = I
Putting the value of k in equation (2) we have
F =ma
S.I. Unit of force: We can derive the S.I. unit of force by taking the mass 1 kg and acceleration, a = 1ms-2.
1 unit force = 1 kg × 1 ms-2 = 1 kg ms-2
This unit of force was given the name Newton and is denoted by ‘N’.
![]()
Question 5.
What is the third law of motion? Give some examples to illustrate it.
Answer:
Newton’s third law of motion: According to the third law of motion, when one object exerts a force on another object then the second object exert a force on the first. These two forces are always equal in magnitude but opposite in direction. This says that the forces always occurs in pairs as result of interaction between them, that is the force act on different objects and not on the same object.
Let two bodies A and B interact with each other. The force exerted by body A on B is called action and the force exerted by the body B on A which is equal to magnitude but opposite in direction is called reaction.
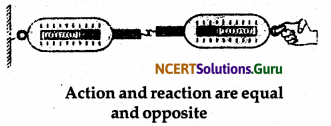
Example: 1. Take two spring balance connected together as shown in the fig. 9.5. The fixed end of the spring balance B attached to a rigid support like ar wall. When a force is applied through the fixed end of the spring balance it shows the same reading on their scale. It means the source exerted by spring balance B on A are equal.
2. A swimmer pushes the water in backward direction with a certain force with his hand (action) and in turn the swimmer is pushed forward due to the reaction of water with the same force.