These NCERT Solutions for Class 9 Science Chapter 8 Motion Questions and Answers are prepared by our highly skilled subject experts to help students while preparing for their exams.
Motion NCERT Solutions for Class 9 Science Chapter 8
Class 9 Science Chapter 8 Motion InText Questions and Answers
Question 1.
An object has moved through a distance. Can it have zero displacement? If yes, support your answer with an example.
Answer:
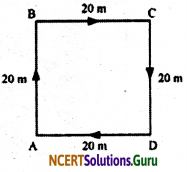
Yes. An object that has moved through a distance can have zero displacement. Displacement is the shortest measurable distance between the initial and the final position of an object. An object which has covered a distance can have zero displacement, if it comes back to its starting point, i.e., the initial position.
Consider the following situation. A man is walking in a square park of length 20 m (as shown in the following figure). He starts walking from point A and after moving along all the corners of the park (point B, C, D), he again comes back to the same point, i.e., A.
In this case, the total distance covered by the man is 20 m + 20 m + 20 + 20 m = 80 m.
However, his displacement is zero because the shortest distance between his initial and final position is zero.
Question 2.
A farmer moves along the boundary of a square field of side 10 m in 40 s. What will be the magnitude of displacement of the farmer at the end of 2 minutes 20 seconds?
Answer:
The farmer takes 40 s to cover 4 × 10 = 40 m.
In 2 min and 20 s (140 s), he will cover a distance = \(\frac{40}{40}\) × 140 = 140 m
Therefore, the farmer completes \(\frac{140}{40}\) rounds (3 complete rounds and a half round) of the field in 2 min and 20 s.
That means, after 2 min 20 s, the farmer will be at the opposite end of the starting point.
Now, there can be two extreme cases.
Case I: Starting point is a corner point of the field.
In this case, the farmer will be at the diagonally opposite comer of the field after 2 min 20 s.
Therefore, the displacement will be equal to the diagonal of the field.
Hence, the displacement will be \(\sqrt{10^{2}+10^{2}}\) = 14.1 m
Case II: Starting point is the middle point of any side of the field.
In this case the farmer will be at the middle point of the opposite side of the field after 2 min 20 s.
Therefore, the displacement will be equal to the side of the field, i.e., 10 m.
For any other starting point, the displacement will be between 14.1 m and 10 m.
Question 3.
Which of the following is true for displacement?
(a) It cannot be zero.
(b) Its magnitude is greater than the distance travelled by the object.
Answer:
(a) Not true
Displacement can become zero when the initial and final position of the object is the same.
(b) Not true
Displacement is the shortest measurable distance between the initial and final positions of an object. It cannot be greater than the magnitude of the distance travelled by an object. However, sometimes, it may be equal to the distance travelled by the object.
![]()
Question 4.
Distinguish between speed and velocity.
Answer:
Speed:
- It refers to the distance travelled by a body in a unit time.
- It is a scalar quantity.
- It is always positive.
Velocity:
- It refers to the net displacement a body undergoes in a unit time.
- It is a vector quantity.
- It can be positive or negative.
Make use of free Average Velocity Calculator to find the average velocity. It will generate the accurate average velocity by taking initial, final velocities.
Question 5.
Under what condition(s) is the magnitude of average velocity of an object equal to its average speed?
Answer:
If the total distance covered by an object is the same as its displacement; then its average speed would be equal to its average velocity.
Question 6.
What does the odometer of an automobile measure?
Answer:
The odometer of an automobile measures the distance covered by an automobile.
Question 7.
What does the path of an object look like when it is in uniform motion?
Answer:
An object having uniform motion has a straight line path.
Question 8.
During an experiment, a signal from a spaceship reached the ground station in five minutes. What was the distance of the spaceship from the ground station? The signal travels at the speed of light, that is, 3 × 108 m s-1.
Answer:
Time taken by the signal to reach the ground station from the spaceship
= 5 min = 5 × 60 = 300 s
Speed of the signal = 3 × 108 m/s
Speed = Speed = \(\frac{\text { Distance travelled }}{\text { Time taken }}\)
∴ Distance travelled = Speed × Time taken = 3 × 108 × 300 = 9 × 1010 m
Hence, the distance of the spaceship from the ground station is 9 × 1010 m.
Question 9.
When will you say a body is in (i) uniform acceleration? (ii) non-uniform acceleration?
Answer:
(i) A body is said to have uniform acceleration if it travels in a straight path in such a way that its velocity changes at a uniform rate, i.e., the velocity of a body increases or decreases by equal amounts in an equal interval of time.
(ii) A body is said to have non-uniform acceleration if it travels in a straight path in such a way that its velocity changes at a non-uniform rate, i.e., the velocity of a body increases or decreases in unequal amounts in an equal interval of time.
![]()
Question 10.
A bus decreases its speed from 80 km h-1 to 60 km h-1 in 5 s. Find the acceleration of the bus.
Answer:
Initial speed of the bus,
u = 80 km/h = 80\(\frac{5}{18}\) = 22.22 m/s
Final speed of the bus,
v = 60km/h = 60 × \(\frac{5}{18}\) = 16.66 m/s
Time take to decrease the speed, t = 5 s
Acceleration a = \(\frac{v-u}{t}=\frac{16.66-22.22}{5}\)
= -1.112 m/s2
Here, the negative sign- of acceleration indicates that the velocity of the car is decreasing.
Question 11.
A train starting from a railway station and moving with uniform acceleration attains a speed 40 km h-1 in 10 minutes. Find its acceleration.
Answer:
Initial velocity of the train, u = 0 (since the train is initially at rest)
Final velocity of the train,
v = 40 km/h = 40 × \(\frac{5}{18}\) = 11.11 m/s
Time taken, t = 10 min = 10 × 60 = 600 s
Acceleration,
a = \(\frac{v-u}{t}=\frac{11.11-0}{600}\) = 0.0185 m/s2
Hence, the acceleration of the train is 0.0185 m/s2.
Question 12.
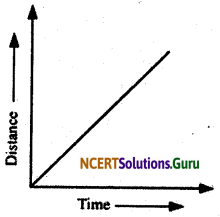
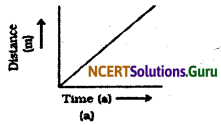
What is the nature of the distance-time graphs for uniform and non-uniform motion of an object?
Answer:
The distance-time graph for uniform motion of an object is a straight line (as shown in the following figure).
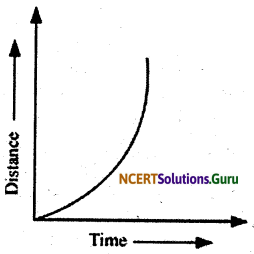
The distance-time graph for non-uniform motion of an object is a curved line (as shown in the given figure).
Question 13.
What can you say about the motion of an object whose distance-time graph is a straight line parallel to the time axis?
Answer:
When an object is at rest, its distance-time graph is a straight line parallel to the time axis.
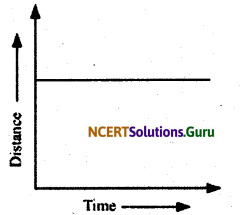
A straight line parallel to the x-axis in a distance-time graph indicates that with a change in time, there is no change in the position of the object. Thus, the object is at rest.
Question 14.
What can you say about the motion of an object if its speed-time graph is a straight line parallel to the time axis?
Answer:
Object is moving uniformly.
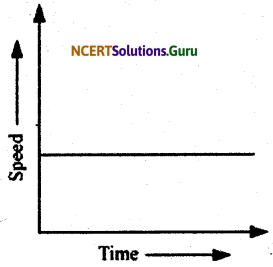
A straight line parallel to the time axis in a speed-time graph indicates that with a change in time, there is no change in the speed of the object. This indicates the uniform motion of the object.
![]()
Question 15.
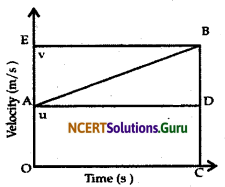
What is the quantity which is measured by the area occupied below the velocity-time graph?
Answer:
Distance
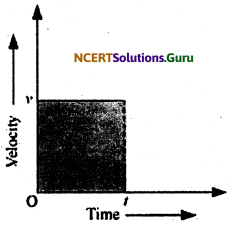
The graph shows the velocity time graph of a uniformly moving body.
Let the velocity of the body at time (t) be v.
Area of the shaded region = length × breath
Where,
Length = t
Breath = v
Area = vt = velocity × time …….. (i)
We know,
Velocity = \(\frac{\text { Displacement }}{\text { Time }}\)
∴ Displacement = Velocity × Time, ……… (ii)
From equations (i) and (ii),
Area = Displacement
Hence, the area occupied below the velocity-time graph measures the displacement covered by the body.
Class 9 Science Chapter 8 Motion Textbook Questions and Answers
Question 1.
A bus starting from rest moves with a uniform acceleration of 0.1 m s-2 for 2 minutes. Find (a) the speed acquired, (b) the distance travelled.
Answer:
(a) 12 m/s (b) 720 m
(a) Initial speed of the bus, u = 0 (since the bus is initially at rest)
Acceleration, a = 0.1 m/s2
Time taken, t = 2 minutes = 120 s
Let v be the final speed acquired by the bus.
∴ a = \(\frac{v-u}{t}\)
0.1 = \(\frac{v-0}{120}\)
(b) According to the third equation of motion: v2 – u2 = 2as
Where, s is the distance covered by the bus (12)2 – (0)2 = 2(0.1)s
s = 720 m
Speed acquired by the bus is 12 m/s.
Distance travelled by the bus is 720 m.
Question 2.
A train is travelling at a speed of 90 km h-1. Brakes are applied so as to produce a uniform acceleration of -0.5 m s-2. Find how far the train will go before it is brought to rest.
Answer:
Initial speed of the train, K = 90 km/h = 25 m/s
Final speed of the train, v = 0 (finally the train comes to rest)
Acceleration = -0.5 m s-2
According to third equation of motion:
v2 = u2 + 2 as
(0)2 = (25)2 + 2 (-0.5) s
Where, s is the distance covered by the train
s = \(\frac{(25)^{2}}{2(0.5)}\) = 625 m
The train will cover a distance of 625 m before it comes to rest.
![]()
Question 3.
A trolley, while going down an inclined plane, has an acceleration of 2 cm s-2. What will be its velocity 3 s after the start?
Answer:
Initial velocity of the trolley, u = 0 (since the trolley was initially at rest)
Acceleration, a = 2 cm s-2 = 0.02 m/s2
Time, t = 3 s
According to the first equation of motion: ν = u + at
Where, ν is the velocity of the trolley after 3 s from start
ν = 0 + 0.02 × 3 = 0.06 m/s
Hence, the velocity of the trolley after 3 s from start is 0.06 m/s.
Question 4.
A racing car has a uniform acceleration of 4 m s-2. What distance will it cover in 10 s after start?
Answer:
Initial velocity of the racing car, u = 0 (since the racing car is initially at rest) Acceleration, a = 4 m/s2
Time taken, t = 10 s
According to the second equation of motion: S= ut + \(\frac {1}{2}\)at2
Where, s is the distance covered by the racing car
Hence, the distance covered by the racing car after 10 s from start is 200 m.
Question 5.
A stone is thrown in a vertically upward direction with a velocity of 5 m s-1. If the acceleration of the stone during its motion is 10 m s-2 in the downward direction, what will be the height attained by the stone and how much time will it take to reach there?
Answer:
Initially, velocity of the stone, u = 5 m/s
Final velocity, ν = 0 (since the stone comes to rest when it reaches its maximum height)
Acceleration of the stone, a = acceleration due to gravity, g = 10 m/s2
(in downward direction)
There will be a change in the sign of acceleration because the stone is being thrown upwards.
Acceleration, a = -10 m/s2
Let s be the maximum height attained by the stone in time t.
According to the first equation of motion:
ν = u + at
0 = 5 + (-10) t
∴ t = \(\frac {-5}{10}\) = 0.5 S
According to the third equation of motion: ν2 = u2 + 2 as
(0)2 = (5)2 + 2 (-10)s
= S = \(\frac {52}{20}\) = 1.25
Hence, the stone attains a height of 1.25 m in 0.5 s.
Question 6.
An athlete completes one round of a circular track of diameter 200 m in 40 s. What will be the distance covered and the displacement at the end of 2 minutes 20 s?
Answer:
Diameter of a circular track, d = 200 m
Radius of the track, r = r = \(\frac{d}{2}\) = 100 m
Circumference = 2πr = 2π (100) = 200π m
In 40 s, the given athlete covers a distance of 200p m.
In 1 s, the given athlete covers a distance = \(\frac{200 \pi}{40} m\)
The athlete runs for 2 minutes 20 s = 140 s
∴ Total distance covered in
s = \(\frac{200 \times 22}{40 \times 7}\) × 140 = 2200m
The athlete covers one round of the circular track in 40 s. This means that after every 40 s, the athlete comes back to his original position. Hence, in 140 s he had completed 3 rounds of the circular track and is taking the fourth round.
He takes 3 rounds in 40 × 3 = 120 s. Thus, after 120 s his displacement is zero.
Then, the net displacement of the athlete is in 20 s only. In this interval of time, he moves at the opposite end of the initial position. Since displacement is equal to the shortest distance between the initial and final position of the athlete, displacement of the athlete will be equal to the diameter of the circular track.
∴ Displacement of the athlete = 200 m
Distance covered by the athlete in 2 min 20 s is 2200 m and his displacement is 200 m.
Question 7.
Joseph jogs from one end A to the other end B of a straight 300 m road in 2 minutes 30 seconds and then turns around and jogs 100 m back to point C in another 1 minute. What are Joseph’s average speeds and velocities in jogging (a) from A to B and (b) from A to C?
Answer:
(a) 2m/s, 2 m/s (b) 1.90 m/s, 0.95 m/s
(a) From end A to end B
![]()
Distance covered by Joseph while jogging from A to B = 300 m
Time taken to cover that distance = 2 min 30 seconds = 150 s
Average speed = \(\frac{\text { Total distance covered }}{\text { Total time taken }}\)
Total distance covered = 300 m
Total time taken = 150 s
Average velocity = \(\frac {300}{150}\) = 2m/s
Average velocity = \(\frac{\text { Displacement }}{\text { Time interval }}\)
Displacement = shortest distance between A and B = 300 m
Time interval = 150 s
Average velocity = \(\frac {300}{150}\) = 2m/s
The average speed and average velocity of Joseph horn A to B are the same and equal to 2 m / s.
(b) From end A to end C
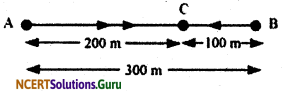
Average speed = \(\frac{\text { Total distance covered }}{\text { total time taken }}\)
Total distance covered = Distance from A to B + Distance from B to C
= 300 + 100 = 400 m
Total time taken = Time taken to travel from A to B + Time taken to travel from B to C = 150 + 60 = 210 s
Average speed = \(\frac {400}{210}\) = 1.90 m/s
Average velocity = \(\frac{\text { Displacement }}{\text { Time interval }}\)
Displacement from A to C = AC = AB – BC = 300 – 100 = 200 m
Time interval = time taken to travel from A to B + time taken to travel from B to C
= 150 + 60 = 210 s
Average velocity = \(\frac {200}{210}\) = 0.95 tn / s
The average speed of Joseph from A to C is 1.90 m/s and his average velocity is 0.95 m/s.
![]()
Question 8.
Abdul, while driving to school, computes the average speed for his trip to be 20 km h-1. On his return trip along the same route, there is less traffic and the average speed is 30 km h-1. What is the average speed for Abdul’s trip?
Answer:
Case I: While driving to school
Average speed of Abdul’s trip = 20 km/h
Average speed = \(\frac{\text { Total distance }}{\text { Total time taken }}\)
Total distance = Distance travelled to reach school = d
Let total time taken = t1
∴ 20\(\frac{d}{t_{1}}\)
t1 = \(\frac{d}{20}\) ………(i)
Case II: While returning from school
Total distance = Distance travelled while returning front school = d
Now, total time taken = t2
30 = \(\frac{d}{t_{2}}\) ……….(ii)
Average speed for Abdul’s trip = \(\frac{\text { Total distance covered in the trip }}{\text { Total timetaken }}\)
Where,
Total distance covered in the trip = d + d = 2d
Total time taken, t = Time taken to go to school + Time taken to return to school
= t1 + t2
∴ Average speed = \(\frac{2 d}{t_{1}+t_{2}}\)
From equations (i) and (ii),
Average Speed = \(\frac{2 d}{\frac{d}{20}+\frac{d}{30}}=\frac{2}{\frac{3+2}{60}}\)
Average Speed = \(\frac {120}{5}\) =24 m/s
Hence, the average speed for Abdul’s trip is 24 m/s.
Question 9.
A motorboat starting from rest on a lake accelerates in a straight line at a constant rate of 3.0 m s-2 for 8.0 s. How far does the boat travel during this time?
Answer:
Initial velocity, u = 0 (since the motor boat is initially at rest)
Acceleration of the motorboat, a = 3 m/s2
Time taken, t = 8 s
According to the second equation of motion:
s = ut + \(\frac {1}{2}\)at2
Distance covered by the motorboat, s
s = 0 + \(\frac {1}{2}\)3(8)2 = 96 m
Hence, the boat travels a distance of 96 m.
Question 10.
A driver of a car travelling at 52 km h-1 applies the brakes and accelerates uniformly in the opposite direction. The car stops in 5 s. Another driver going at 3 km h-1 in another car applies his brakes slowly and stops in 10 s. On the same graph paper, plot the speed versus time graphs for the two cars. Which of the two cars travelled farther after the brakes were applied?
Answer:
Case A:
Initial speed of the car, u1 = 52 km/h = 14.4 m/s
Time taken to stop the car, t1 = 5 s
Final speed of the car becomes zero after 5 s of application of brakes.
Case B:
Initial speed of the car, u2 = 3 km/h = 0.833 m/ss ≅ 0.83 m/s
Time taken to stop the car, t2 = 10 s
Final speed of the car becomes zero after 10 s of application of brakes.
Plot of the two cars on a speed-time graph is shown in the following figure:
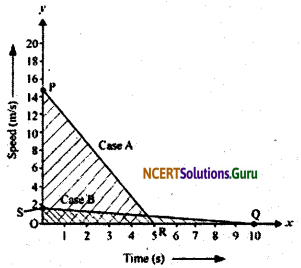
Distance covered by each car is equal to the area under the speed-time graph.
Distance covered in case A,
s1 = \(\frac {1}{2}\) × OP × OR = \(\frac {1}{2}\)14.4 × 5 = 36 m
Distance covered in case B,
s2 = \(\frac {1}{2}\) × OS × OQ = \(\frac {1}{2}\) × 0.83 × 10 = 4.15m
Area of ΔOPR > Area of ΔOSQ
Thus, the distance covered in case A is greater than the distance covered in case B.
Hence, the car travelling with a speed of 52 km/h travels farther after brakes were applied.
Question 11.
Fig 8.11 shows the distance-time graph of three objects A, B and C. Study the graph and answer the following questions:
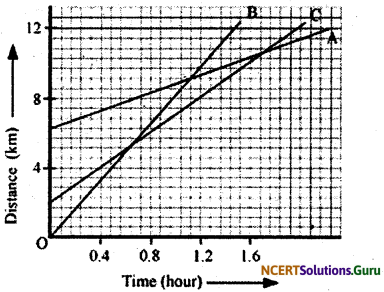
(a) Which of the three is travelling the fastest?
(b) Are all three ever at the same point on the road?
(c) How far has C travelled when B passes A?
(d) How far has B travelled by the time it passes C?
Answer:
(a) Object B
(b) No
(c) 5.714 km
(d) 5.143 km
(a) Speed = \(\frac{\text { Distance }}{\text { Time }}\)
slope of the graph = \(\frac{y-\text { axis }}{x- \text { axis }}=\frac{\text { Distance }}{\text { Time }}\)
∴ Speed = slope of the graph
Since slope of object B is greater than objects A and C, it is travelling the fastest.
(b) AD three objects A, B and C never meet at a single point. Thus, they were never at the same point on road.
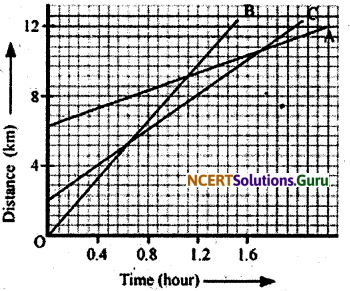
(c)
On the distance axis:
7 small boxes = 4 km
∴ 1 small box = \(\frac {4}{7}\) km
Initially, object C is 4 blocks away from the origin.
∴ Initial distance of object C from origin = \(\frac {16}{7}\) km
Distance of object C from origin when B passes A = 8 km
Distance covered by C
= \(8-\frac{16}{7}=\frac{56-16}{7}=\frac{40}{7}\) = 5.714 km
Hence, C has travelled a distance of 5.714 km when B passes A.
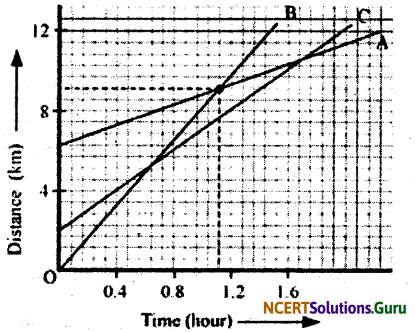
(d)
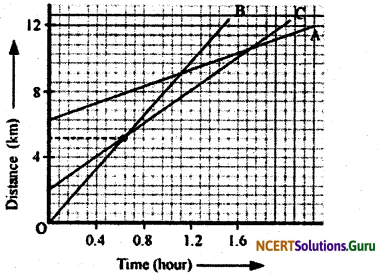
Distance covered by B at the time it passes C = 9 boxes
= \(\frac {4}{7}\) × 9 = \(\frac {36}{7}\) = 5.143 km
Hence, B has travelled a distance of 5.143 km when B passes A.
![]()
Question 12.
A ball is gently dropped from a height of 20 m. If its velocity increases uniformly at the rate of 10 m s-2, with what velocity will it strike the ground? After what time will it strike the ground?
Answer:
Distance covered by the ball, s = 20 m
Acceleration, a= 10 m/s
Initially, velocity, u = 0 (since the ball was initially at rest)
Final velocity of the ball with which it strikes the ground, v
According to the third equation of motion:
ν2 = u2 + 2 as
ν2 = 0 + 2 (10) (20)
v = 20 m/s
According to the first equation of motion:
ν = u + at
Where,
Time, f taken by the baU to strike the ground is,
20 = 0 + 10(t)
t = 2s
Hence, the ball strikes the ground after 2 s with a velocity of 20 m/ s.
Question 13.
The speed-time graph for a car is shown is Fig. 8.12.
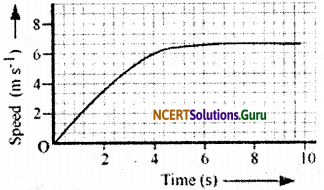
(a) Find out how far the car travels in the first 4 seconds. Shade the area on the graph that represents the distance travelled by the car during the period.
(b) Which part of the graph represents uniform motion of the car?
Answer:
(a)
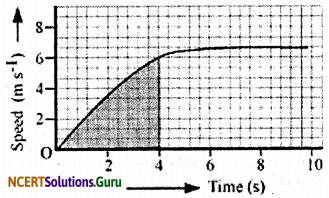
The shaded area which is equal to represents the distance travelled by the car in the first 4 s.
(b)
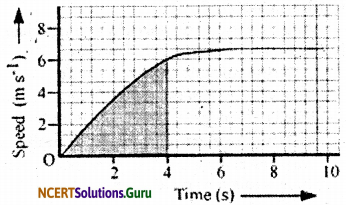
The part of the graph in red colour between time 6 s to 10 s represents uniform motion of the car.
Question 14.
State which of the following situations are possible and give an example for each of these:
(a) an object with a constant acceleration but with zero velocity.
(b) an object moving in a certain direction with an acceleration in the perpendicular direction.
Answer:
(a) Possible:
When a ball is thrown up at maximum height, it has zero velocity, although it will have constant acceleration due to gravity, which is equal to 9.8 m/s2.
(b) Possible:
When a car is moving in a circular track, its acceleration is perpendicular to its direction.
Question 15.
An artificial satellite is moving in a circular orbit of radius 42250 km. Calculate its speed if it takes 24 hours to revolve around the earth.
Answer:
Speed = \(\frac{\text { Distance }}{\text { Time }}\)
r Time
Distance = 2πr = 2 × 3.14 × 42 × 42250 = 265330 km
Time = 24 h
Speed = \(\frac{265330}{24}\) = 11055.4 km/h
Class 9 Science Chapter 8 Motion Additional Important Questions and Answers
Multiple choice Questions
Question 1.
The change in velocity of an object per unit time is called
(a) Average velocity
(b) Acceleration
(c) Force
(d) Momentum
Answer:
(b) Acceleration
Question 2.
If the distance-time graph of a body ¡s parabola, then its motion is
(a) Uniform
(b) Non-uniform
(d) Body’s in rest
(d) Body is in vibratory motion
Answer:
(a) Uniform
![]()
Question 3.
Retardation is
(a) Positive acceleration
(b) Zero acceleration
(c) Non-uniform acceleration
(d) Zero acceleration
Answer:
(b) Zero acceleration
Question 4.
If the displacement of an object is proportional to square of time, then the object moves with
(a) uniform velocity
(b) uniform acceleration
(c) increasing acceleration
(d) decreasing acceleration,
Answer:
(b) uniform acceleration
Question 5.
Suppose a boy is enjoying a ride on a merry-go-round which is moving with a constant speed of 10 ms-1. It implies that the boy is
(a) at rest
(b) moving with no acceleration
(c) in accelerated motion
(d) moving with uniform velocity
Answer:
(c) in accelerated motion
Question 6.
In which of the following cases of motions, the distance moved and the magnitude of displacement are equal?
(a) If the car is moving on straight road
(b) If the car is moving in circular path
(c) The pendulum is moving to and fro
(d) The earth is revolving around the Sun
Answer:
(a) If the car is moving on straight road
Question 7.
When a body completes one round in a circular path of radius ‘r’, its displacement is equal to
(a) r
(b) 2r
(c) 2nr
(d) Zero
Answer:
(d) Zero
Question 8.
The S.I. unit used to express acceleration is
(a) ms
(b) ms-1
(c) Ms-2
(d) m2m-1
Answer:
(c) Ms-2
Question 9.
A body falls freely from a point and reaches the ground in 1 second, then the height of the point from the earth is equal to
(a) 9.8 m
(b) 4.9 m
(c) 10m
(d) 19.6 m
Answer:
(b) 4.9 m
![]()
Question 10.
A body starts moving from rest with a uniform acceleration of 2ms-2.
(a) 6 m
(b) 9m
(c) 12 m
(d) 18 m
Answer:
(b) 9m
Question 11.
Which of the following figures (Fig.) represents uniform motion of a moving object correctly?
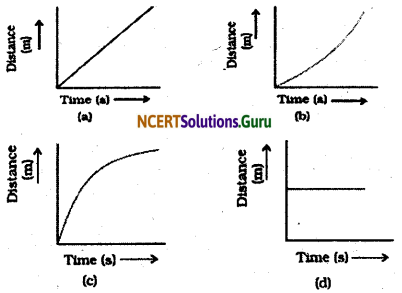
Answer:
Question 12.
Which of the following is a vector quantity?
(a) Speed
(b) Distance
(c) Velocity
(d) energy
Answer:
(a) Speed
Very Short Answer Type Questions
Question 1.
How will you describe the position of an object?
Answer:
The position of an object can only be described with respect to a fixed point called reference point or origin.
Question 2.
When is the motion of a body said to be rectilinear motion?
Answer:
When a body moves in a straight line, its motion is said to be rectilinear motion.
Question 3.
Define velocity. Give its S.I. unit.
Answer:
Velocity is defined as the displacement produced per unit time. It’s S.I. unit is ms-1.
![]()
Question 4.
Define acceleration. Give its S.I. unit.
Answer:
The change in velocity of an object per unit time is called its acceleration.
Acceleration = \(\frac{\text { Final velocity – Intitial velocity }}{\text { Time }}\)
It’s S.I. unit is ms-2.
Question 5.
What does the slope of the following graphs indicate?
(a) Distance-time graph passing through the origin and making an angle with the time axis.
(b) Speed-time graph making an angle with lime axis and a straight line passing through the origin.
Answer:
(a) Speed of the object.
(b) Acceleration of the object.
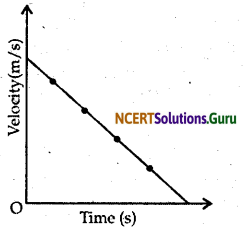
Question 6.
Draw a velocity-time graph showing negative acceleration of the body.
Answer:
Question 7.
The graph of two friends A and B are shown in the figure 8.13 below:
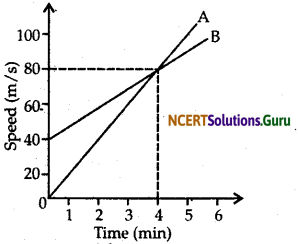
(a) Which of the two friends is moving faster?
(b) Where and when will they meet?
Answer:
(a) A is moving faster than B because of its greater slope.
(b) The two will meet after 4 minutes at distance of 80 meters.
Question 8.
What does the following graph indicate?
(a) Distance-time graph is a straight line making an angle with time-axis
(b) Speed-time graph is a straight line making an angle with the time-axis and passing through the origin.
Answer:
(a) Uniform motion of body.
(b) Uniform positive acceleration.
Question 9.
Draw a graph describing the osillatory motion of a body.
Answer:
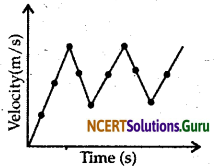
Question 10.
What is the nature of uniform circular motion?
Answer:
The uniform circular motions are always accelerated motion.
Short Answer Type Questions
Question 1.
When is a body said to be in motion? Explain with an example that the motion of a body is relative to the position of other objects.
Answer:
A body is said to be in motion if its position continues to change with the surroundings. Motion is relative i.e. an object/ body may appeard to be moving to some but not others. Such as two students travelling in a bus while sitting on same seat. For people outside they are in motion but with respect to each other, the two friends are in state of rest.
![]()
Question 2.
What do you mean by distance and displacement? How are they different?
Answer:
The length of the actual path travelled or covered between initial and final position of an object is called distance.
The change in position of an object is a given direction from its initial position is called displacement.
The differences between distance and displacements are:
| Distance | Displacement |
| 1. It refers to the actual length covered by a body between its initial and final position. | It refers to the minimum distance between initial and final position of the body. |
| 2. It’s a scalar quantity. | It’s a vector quantity. |
| 3. It is always positive. | It can be positive or negative. |
Question 3.
A bus starts from point A and goes to point B after travelling 60 km on a straight road and then returns to point A.
(i) What is the total distance covered by the bus?
(ii) What is its displacement?
Answer:
(i) Total distance travelled by bus from A to B and back to point A, then
AB + BA = 60m + 60m = 120m
(ii) The net displacement is zero because the final position coincides with initial position.
Question 4.
What do you mean by uniform and non-uniform acceleration?
Answer:
Uniform motion: When a body covers equal distance in equal interval of time, how small time interval may be, the motion is called uniform motion.
If a body covers 60 km in an hour moving with a uniform motion, then it would cover 30 km in half hour and 15 km in 15 minutes.
Non-uniform motion: A body is said to be in non-uniform motion which it covers unequal distances in equal interval of time or regular changes its direction. Most of the motion we see in daily life like that of vehicles on city roads are non-uniform motion.
![]()
Question 5.
What is the speed and average speed of a body in motion?
Answer:
The distance covered by a body in motion in unit time is called its speed.
Speed = \(\frac{\text { Distance travelled }}{\text { Time }}\)
If a car covers 40 km in 1st hours, 60 km in 2nd hour and 50 km in 3rd hour, then its, average speed is
\(\frac{40+60+50}{3}\) = 50 km/h
Question 6.
On a stormy night, the ligtning is seen first and thunder is heard later, though they are produced simultaneously at same time. Why?
Answer:
The lightning is seen first and thunder is heard later because of the difference in speed of light and sound. The light travelling with speed of 3 × 108 ms-1 reaches the earth earlier than sound travelling with speed of 340 ms-1.
Question 7.
On a rainy day, the sound of thunder is heard after 5 seconds of the flash of lightning. :
Calculate the distance of the nearest point of ligtning.
Answer:
In atmosphere, lightning and thunder occur at same time.
Time taken by sound to reach to earth = 5s
Speed of sound = 346 ms-1
∴ Distance of nearest point of lightning = 346 × 5 = 1730 m
Question 8.
What do you mean by positive and negative acceleration? Give examples.
Answer:
When the acceleration of a body increases with time, it is called positive aceleration such as the free falling body experiences an increase in its velocity by 9.8 m/s, every second.
When the acceleration of a body decreases with time, it is called negative acceleration such as the stopping of car after application of breakes in time t, covering a distance of s metres.
Question 9.
Give examples of the following motion:
(a) Uniform motion in a straight line in which the velocity is increasing
(b) A body moving with constant speed in which velocity is changing at uniform rate.
(c) Non-uniform motion with constant acceleration in the direction of motion.
(d) Non-uniform motion in which acceleration is not constant.
Answer:
(a) The motion of a train between two stations on a straight track between certain interval of time when its velocity becomes constant is an example of uniform motion in which velocity remains constant.
(b) When a body is moving in a circular path with constant speed, its direction changes at every point hence, due to change in its direction, its velocity also changes simultaneously.
(c) The motion of a free falling body is an example of non-uniform motion with the constant acceleration in tire direction of motion as it fall downward with constant acceleration of 9.8 ms-2 due to gravity of the earth.
(d) When a train starts moving from a railway station, it increases its speed by unequal amount in equal interval of time till it attains the maximum speed.
![]()
Question 10.
What is the importance of graphs in daily life.
Answer:
A graph provides a convenient method to represent pictorially the basic information about an event. A graph can be bar graph, line graph or a pie chart. These graphs are used in:
- Comparing and solving the linear motion and equations with two variable.
- Finding the motion of a body to be uniform or non-uniformotion.
- Calculating the distance travelled by a body from speed-time graph.
Question 11.
Draw the distance-time graph of a uniform motion. How will you calculate the speed of the object from this graph.
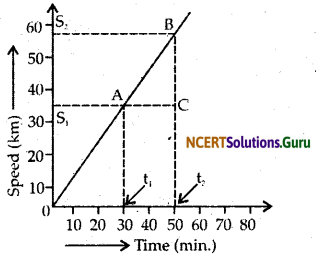
Answer:
Tire given graph is the distance time graph. To determine the speed of object between A and B, draw,a line from A, parallel to X-axis and an another line parallel to speed-axis from point B. These two lines meet at point C and form a triangle ABC. In ΔDBC, AC denotes the time interval and BC denotes the distance travelled. Hence,
Speed (V) = \(\frac{\mathrm{BC}}{\mathrm{AC}}=\frac{S_{2}-S_{1}}{t_{2}-t_{1}}\) Sloped line A
Question 12.
The time of arrival and departure of a train at three station A, B and C and their distances from station A are given the table below. Plot the distance for graph for the motion of the tain assuming that its motion between the onation is uniform.
| Station | Distance from Station | Time of arrival | Time of departure |
| A | 0 km | 8 : 00 | 8 : 15 |
| B | 120 km | 11 : 15 | 11 : 30 |
| C | 180 km | 13 : 00 | 13 : 15 |
Answer:
The distance timetable for the motion of the train

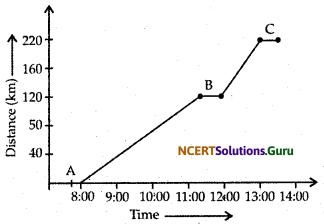
Question 13.
Megha and his sister Anu goes to the school on bicycle. Both of them start at the same time but take different time to reach the school although they follow the same route. Table below shows the distance moved by both at different instant of time, plot the distance-time graph for their motion on the same graph and interpret the graph.

Answer:
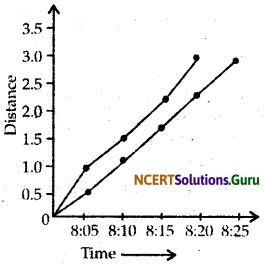
The distance-time gaph shows both are moving with non-uniform motion. The average speed of Megha is greater than that of Anu.
![]()
Question 14.
The average walking speed of a boy while going to school is 4 km/h. It take half an hour to reach the school. Calculate the school’s distance from home.
Answer:
Average speed of the boy = 4 km/h
Time taken to reach school = \(\frac {1}{2}\) hour
Distance of school from house = Speed × Time
= 4 km/h × \(\frac {1}{2}\) hour = 2 km
Question 15.
The odometer of a car reads 2000 km from the start of a trip by John. The trip takes 8 hours and shows reading of 2400 km. What is the average speed of John’s car in km/h and m/ s?
Answer:
Distance covered by car = Final reading – Initial read
= 2400 – 2000 = 400 km
Time taken by John to cover 400 km = 8 hr
∴ Average speed = \(\frac{400 \mathrm{~km}}{8 \mathrm{hr}}\) = 50km/hr
Average speed (in ms-11) \(\frac{50 \times 1000}{60 \times 60}\) = 13.9 ms-1
Question 16.
Usha swims in a 90 m long swimming pool. She covers 180 m in one minute swimming from one end of pool and back to the pool along a straight path. Find the average speed and average velocity?
Answer:
Total distance covered by Usha in one minium = 180 m.

Question 17.
Narang is moving his car with a velocity of 90 km/h. How much distance will he cover in (a) one minute (b) one second.
Answer:
Velocity of car = 90 km/h
(a) Distance covered in one minute
= \(\frac{90}{60}=\frac{3}{2}=\frac{3 \times 1000}{2}\) = 1500 m
(b) Distance covered in one second
\(\frac{90}{60 \times 60} k m=\frac{90 \times 1000}{60 \times 60}\) = 25 m
Question 18.
An electric train is moving with an aver age velocity of 120 km/h. How much distance will it cover in 30s ?
Answer:
Velocity of train (V) = 120 km/h.
= \(\frac{120 \times 1000}{60 \times 60}=\frac{100}{3} \mathrm{~m} / \mathrm{s}\)
Time taken = 30s
∴ Distance covered in 30s
= Average × Time velocity = \(\frac {100}{3}\) × 30 = 1000 m
Question 19.
In a long distance race, the athletes were expected to take four rounds of the track such that the line of finish was same as the line of start. The length of track is 200 m.
(a) Calculate the total distance covered by the athletes.
(b) Displacement of athletes when they touch the finishing line.
(c) Is the motion of athletes uniform or non-uniform?
Answer:
(a) In four rounds, total distance covered
= 4 × length of track = 4 × 200 = 800 m
(b) Displacement upon touching the finishing line would be zero as track is a circular track.
(c) Motion of athletes would be non-uniform as they are not completing the race at the same time i.e. distance covered by them in equal interval of time is not equal.
![]()
Question 20.
A circular track has a circumference of 314 m with AB as one of its diameter. A cyclist traveels from A to B along the circular path in 30s. Find
(a) Speed of cyclist.
(b) Displacement of cyclist.
Answer:
(a) Circumference of circular track = 314
∴ Distance from A to B = \(\frac {314}{2}\) = 157 m.
Time taken by cyclist = 30 s.
Time = \(\frac{\text { Distance }}{\text { Time }}=\frac{157}{30}\) = 5.23 m/s
(b) Diplsacement of cyclist from A to B which represents diameter of circular track
2πr = 314
2 × 3.14 × r =314
r = \(\frac{314}{3.14 \times 2}\) = 50m
When r = 50 m, d = 2r = 50 × 2 = 100 m
Question 21.
A car travels a certain distance at an average speed of 30 km/h and returns back with an average speed of 50 km/h. Calculate the average speed of car.
Answer:
Let distance covered by car travelling at 30 km/h = x
∴ Time taken = \(\frac{x}{30}\)h
Similarly when coming back time taken = \(\frac{x}{50}\)h
Total time taken = \(\frac{x}{30}+\frac{x}{50}=\frac{5 x+3 x}{150}=\frac{8 x}{150} h\)
Total distance covered = x + x = 2x
Average speed of car = \(\frac{2 x}{8 x / 50}=\frac{2 x \times 150}{8 x}=\frac{75}{2}\) = 37.5 km/h
Question 22.
Rahul starting from rest paddles his bicycle to attain a velocity of 6 m s-1 in 30s. Then he applies brakes so that the velocity of bicycle comes to 4ms-1 in next 5 seconds. Calculate acceleration of bicycle in both cases.
Answer:
In first case, initial velocity (u) = 0
Final velocity (ν) =6 ms-1
Time taken = 30s
Acceleration (a) = ?
We know that,
a = \(\frac{v-u}{t}\)
d = \(\frac{6-0}{30}=\frac{1}{5}\) = 0.2 ms-1
In second case, u = 6ms-1, ν = 0.2 ms-1,
Time = 68
∴ a = \(\frac{4-6}{5}=\frac{-2}{5}\) = -0.4 ms-2
Question 23.
A train starting from rest attains a velocity of 72 km/h in 5 minutes. Assuming that the acceleration is uniform, find (i) the acceleration and distance travelled by the train while attaining this velocity.
Answer:
Initial velocity, u = 0 final velocity (ν) = 72 km/h
Time (t) = 5 minutes = 5 × 60 = 300 s
Acceleration (a) = ?
a = \(\frac{v-u}{t}=\frac{20-0}{300}=\frac{1}{15} m s^{-2}\)
Let distance travelled by train = S
2as = ν2 – u2
2 × \(\frac {1}{5}\) × 5 = (20)2 (72 km/h = 20 mis)
S = 2 × \(\frac {1}{5}\) × 5 = 3000m = 3 km.
Question 24.
A can accelerates uniformly from 18 km/h to 36 km/h in 5 seconds. Calculate (i) The acceleration, (ii) Distance covered by car is that time.
Answer:
Initial velocity of car (h) = 18 km/h
= \(\frac{18 \times 100}{60 \times 60} 5 \mathrm{~m} / \mathrm{s}\)
Final velocity of car (ν) =36 km/h
= \(\frac{36 \times 100}{60 \times 60}=10 \mathrm{~m} / \mathrm{s}\)
Time (t) = 5s.
(i) ∴ Acceleration, a = \(\frac{v-u}{t}=\frac{10-5}{5} 1 \mathrm{~ms}^{-2}\)
(ii) Let distance covered by car = S
2as = ν2 – u2
2 × 1 × s = (10)2 – (5)2
2 × 1 × s = 100 – 25
s = \(\frac {75}{2}\) = 37.5m
![]()
Question 25.
The brakes applied to a car produce a negative acceleration of – 6 m/s2. The car takes 2 seconds to stop after applying the brakes. Calculate the distance it would cover before coming to a stop.
Answer:
Acceleration of car, a = – 6 ms-2
Time taken by car to stop = 2s
Final velocity ν = 0
We know that
ν = u + at
= 4 – 6 × 2
or u = 12m/s
Let distance covered = s
u = ut + \(\frac {1}{2}\)at–
s = 12 × 2 + \(\frac {1}{2}\) × (6) × (2)–
= 24 + 12 = 36 m.
Question 26.
Find the initial velocity of car which is stopped in 10 seconds after appplication of brakes. Also calculate the distance travelled by the car if its negative acceleation is – 2.5 ms-2.
Answer:
Final velocity (ν) = 0
Let initial velocity =u
Acceleration (a) = -2.5 ms-2
Time taken (t) = 10 seconds
We know that,
ν = u + at
0 = u – 2.5 × 10
u = 25 ms-1
Let distance covered = s
s = ut + \(\frac {1}{2}\)at2
= 25 x 10 –\(\frac {1}{2}\) × 2.5(10)2
= 250 + 125 = 375 m
Question 27.
A ball is thrown upward with initial velocity of 90 km/h in upward direction. Calculate
(i) Maximum height reached.
(ii) Time taken to reach the maximum height.
Answer:
Initial velocity of ball, u = 90 km/h
= \(\frac{90 \times 1000}{3600}=25 \mathrm{~m} / \mathrm{s}\)
Final velocity of ball, ν = 0 (at max height)
Acceleration, a = -10ms-2
Let the height gained by ball = s
2as = ν2 – u2
2 × (-10) × s = 0 – (25)2
– 20S = – 625
s = \(\frac {625}{20}\) = 31.25 m
Let time taken to achieve the height = t
ν = u + at
0 = 25 – 10 × t
t = \(\frac {25}{10}\) = 2.5
Question 28.
Can the average speed of a moving object be zero? Can the average velocity of a moving object be zero? Give example.
Answer:
The average speed of a moving object cannot be zero while the average velocity of a moving object can be zero.
A car start from point A and travels 40 km in an hour and then returns to point A again in 40 minutes.
Then Average speed = \(\frac{(40+40) \mathrm{km}}{1.40 \mathrm{hr}}=\frac{80}{1.40} \mathrm{hr}=57.14 \mathrm{~km} / \mathrm{hr}\)
The displacement produced after the comple-tion of return to point A = 0.
Average velocity = \(\frac{\text { Total displacement }}{\text { Total time }}\) = 0.
Question 29.
A radar spots an enemy plane. A radio pulse emitted by radar and reflected by the plane reaches back in 0.5 x 10-3 s. Find the distance between plane and radar.
(Speed of radar pulse = 3 × 108 m/s)
Answer:
Total time taken for pulse to reach and get reflected = 0.5 × 10-3 s
= \(\frac{0.5 \times 10^{-3}}{2}\)
Distance = Speed × Time
= 3 × 108 × \(\frac{0.5 \times 10^{-3}}{2}\) = 0.75 × 105m = 7.5 km
![]()
Question 30.
Draw a velocity time graph for a uniformly accelerated motion. How will you determine the distance covered by a body in a given interval of time using the graph.
Answer:
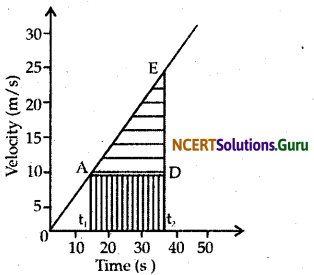
The velocity time graph for uniformly accelerated motion is a straight line curve passing through the origin and makes an angle with time axis. Using the graph, the distance travelled by a body between any given time interval can eas easily be determined.
Let the time interval be t1 and t2 The distance covered would be equal to area of ABCDE
Area of ABCDE = Area of ΔADE + Area of rectangle ABCD
= \(\frac {1}{2}\) (AD × DE) + (AB × BC)
Long Answer Type Questions
Question 1.
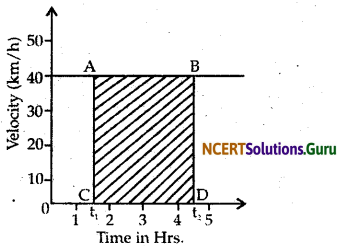
Draw a velocity time graph of a car moving with uniform velocity of 40 km/h. Using the graph determine the distance travelled by car in a given time interval of t1 and t2.
Answer:
The velocity-time graph of a car moving with the uniform velocity shown in the figure the graph is parallel to time-axis.
To determine the distance travelled between the time interval t1 and t2, perpendicular are drawn from point t1 and t2 on the graph.
Distance travelled = Velocity × time
= AC × CD = 40 × (t2 – t1) km
= Area of rectangle ABCD
Question 2.
Derive the relation V = u + at from the velocity-time graph for uniform motion.
Answer:
The velocity-time graph for a uniformly accelerated motion is given in figure. A represents
initial velocity and B represent final velocity in time t shown by OC.
Draw AD || OC, so that
BD + DC = BC or
BA + CA = BC
If BC = u, OA = u
Them ν = BD + u
ν – u = BD ….. (i)
But accleration (a) = \(\frac{\text { Change in velocity }}{\text { Time }}\)
= \(\frac{\mathrm{BD}}{\mathrm{AD}}=\frac{\mathrm{BD}}{\mathrm{BC}}\)
or a = \(\frac{\mathrm{BD}}{\mathrm{t}}\)
BD = at
or ν = u + at
![]()
Question 3.
Derive the relation s = ut + 1at2 from velocity-time graph of a uniform accelerated motion.
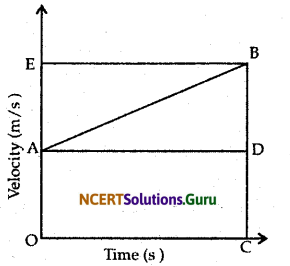
Answer:
The velocity-time graph for a uniform accelerated motion is shown in figure. Initial velocity = u, at point A,
Final velocity = ν, at point B
Time = t
From point, perpendicular BL is drawn on time-axis and BE on velocity-axis respectively. OA represents initial velocity OE or BC represents final velocity in time interval, t or OC.
The distance travelled by object is given by the area enclosed with in OBC under the velocity time graph AB.
Area of OBC = Area of rectangle OADC + Area of ΔADB
= (OA × OC) + \(\frac {1}{2}\)(AD × BD)
Acceleration (a)

Question 4.
Derive the relation v2 – u2 = 2a from velocity-time graph of a uniformly accelerated motion.
Answer:
The velocity time graph of an acclerated motion is shown in the figure.
The distance covered by object moving under uniform accleration ‘a’ is given by area of trapezium OABC
∴ Distance s = \(\frac {1}{2}\)(OA + BC) × OC
OA = u, BC = ν and OC = t
s = \(\left(\frac{u+v}{a}\right) \times t\)
But we know ν = u + at