NCERT Solutions for Class 9 Science Chapter 10 Gravitation

These NCERT Solutions for Class 9 Science Chapter 10 Gravitation Questions and Answers are prepared by our highly skilled subject experts to help students while preparing for their exams.

Gravitation NCERT Solutions for Class 9 Science Chapter 10

Class 9 Science Chapter 10 Gravitation InText Questions and Answers

Question 1.
State the universal law of gravitation.
Answer:
The universal law of gravitation states that every object in the universe attracts every other object with a force called the gravitational force. The force acting between two objects is directly proportional to the product of their masses and inversely proportional to the square of the distance between their centers.

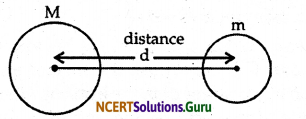
For two objects of masses ml and m2 and the distance between them r, the force (F) of attraction acting between them is given by the universal law of gravitation as:
F = \(\frac{G m_{1} m_{2}}{r^{2}}\)

Where, G is the universal gravitation constant given by:
G = 6.67 × 10^-11 Nm² kg^-2

Question 2.
Write the formula to find the magnitude of the gravitational force between the earth and an object on the surface of the earth.
Answer:
Let ME be the mass of the Earth and m be the mass of an object on its surface. If R is the radius of the Earth, then according to the universal law of gravitation, the gravitational force (F) acting between the Earth and the object is given by the relation:
F = \(\frac{G m_{1} m_{2}}{r^{2}}\)

Question 3.
What do you mean by free fall?
Answer:
Gravity of the Earth attracts every object towards its centre. When an object is released from a height, it falls towards the surface of the Earth under the influence of gravitational force. The motion of the object is said to have free fall.

Question 4.
What do you mean by acceleration due to gravity?
Answer:
When an object falls towards the ground from a height, then its velocity changes during the fall. This changing velocity produces acceleration in the object. This acceleration is known as acceleration due to gravity (g). Its value is given by 9.8 m/s².

Question 5.
What are the differences between the mass of an object and its weight?
Answer:
Mass:

1. It refer to quantity contained in an object
2. It is a scalar quantity.
3. It’s S.I. unit is Kg.
4. It remains constant at places.
5. It is measured by physical or beam balance

Weight:

1. It refers to force with which a body is attracted towards the earth.
2. It is a vector quantity
3. It’s S.I. unit is Newton.
4. It varies depending upon the value of g.
5. It is measured by spring balance.

Question 6.
Why is the weight of an object on the moon \(\frac {1}{6}\)th its weight on the earth?
Answer:
Let ME be the mass of the Earth and m be an object on the surface of the Earth. Let RE be the radius of the Earth. According to the universal law of gravitation, weight W_E of the object on the surface of the Earth is given by,
W_E = \(\frac{\mathrm{GM}_{\mathrm{E}} m}{\mathrm{R}_{\mathrm{E}}{ }^{2}}\)
Let M_M and R_M be the mass and radius of the moon.
Then, according to the universal law of gravitation, weight W_M of the object on the surface of the moon is given by,
W_M = \(\frac{\mathrm{GM}_{\mathrm{E}} m}{\mathrm{R}_{\mathrm{M}}{ }^{2}}\)
\(\frac{W_{M}}{W_{\mathrm{E}}}=\frac{M_{\mathrm{M}} R_{\mathrm{E}}{ }^{2}}{\mathrm{~W}_{\mathrm{E}} \mathrm{R}_{\mathrm{M}}{ }^{2}}\)
Where, ME = 5.98 × 10²⁴ kg, MM = 7.36 × 10²² kg
R_E = 6.4 × 10⁶ m, R_M = 1.74 × 10⁶ m
∴ \(\frac{W_{M}}{W_{\mathrm{E}}}=\frac{7.36 \times 10^{22} \times\left(6.37 \times 10^{6}\right)^{2}}{5.98 \times 10^{24} \times\left(1.74 \times 10^{6}\right)^{2}}=0.165 \approx \frac{1}{6}\)
Therefore, weight of an object on the moon is \(\frac {1}{6}\) of its weight on the Earth.

Question 7.
Why is it difficult to hold a school bag having a strap made of a thin and strong string?
Answer:
It is difficult to hold a school bag having a thin strap because the pressure on the shoulders is quite large. This is because the pressure is inversely proportional to the surface area on which the force acts. The smaller is the surface area; the larger will be the pressure on the surface. In the case of a thin strap, the contact surface area is very small. Hence, the pressure exerted on the shoulder is very large.

Question 8.
What do you mean by buoyancy?
Answer:
The upward force exerted by a liquid on an object immersed in it is known as buoyancy. When you try to immerse an object in water, then you can feel an upward force exerted on the object, which increases as you push the object deeper into water.

Question 9.
Why does an object float or sink when placed on the surface of water?
Answer:
If the density of an object is more than the density of the liquid, then it sinks in the liquid.

This is because the buoyant force acting on the object is less than the force of gravity. On the other hand, if the density of the object is less than the density of the liquid, then it floats on the surface of the liquid. This is because the buoyant force acting on the object is greater than the force of gravity.

Question 10.
You find your mass to be 42 kg on a weighing machine. Is your mass more or less than 42 kg?
Answer:
When you weigh your body, an upward force acts on it. This upward force is the buoyant force. As a result, the body gets pushed slightly upwards, causing the weighing machine to show a reading less than the actual value.

Question 11.
You have a bag of cotton and an iron bar, each indicating a mass of 100 kg when measured on a weighing machine. In reality, one is heavier than other. Can you say which one is heavier and why?
Answer:
The bag of cotton is heavier than the iron bar. This is because the surface area of the cotton bag is larger than the iron bar. Hence, more buoyant force acts on the bag than that on an iron bar. This makes the cotton bag heavier than its actual value. For this reason, the iron bar and the bag of cotton show the same mass on the weighing machine, but actually the mass of cotton bag is more than that of the iron bar.

Class 9 Science Chapter 10 Gravitation Textbook Questions and Answers

Question 1.
How does the force of gravitation between two objects change when the distance between them is reduced to half?
Answer:
According to the universal law of gravitation, gravitational force (F) acting between two objects is inversely proportional to the square of the distance (r) between them, i.e.,
F ∝ \(\frac{1}{r^{2}}\)
If distance r becomes r/2, then the gravitational force will be proportional to
\(\frac{1}{\left(\frac{r}{2}\right)^{2}}=\frac{4}{r^{2}}\)
Hence, if the distance is reduced to half, then the gravitational force becomes four times larger than the previous value.

Question 2.
Gravitational force acts on all objects in proportion to their masses. Why then, a heavy object does not fall faster than a light object?
Answer:
All objects fall on ground with constant acceleration, called acceleration due to gravity (in the absence of air resistance). It is constant and does not depend upon the mass of an object. Hence, heavy objects do not fall faster than light objects.

Question 3.
What is the magnitude of the gravitational force between the earth and a 1 kg object on its surface? (Mass of the earth is 6 × 10²⁴ kg and radius of the earth is 6.4 × 10⁶ m).
Answer:
According to the universal law of gravitation, gravitational force exerted on an object of mass m is given by:
F = \(\frac{\mathrm{GMm}}{r^{2}}\)
Where,
Mass of Earth, M = 6 × 10²⁴ kg
Mass of object, m = 1 kg
Universal gravitational constant, G = 6.7 × 10^-11 Nm² kg^-2
Since the object is on the surface of the Earth, r = radius of the Earth (R)
r = R = 6.4 × 10⁶ m
Gravitational force, F = \(\frac{\mathrm{GMm}}{\mathrm{R}^{2}}\)
= \(\frac{6.7 \times 10^{-11} \times 6 \times 10^{24} \times 1}{\left(6.4 \times 10^{6}\right)^{2}}\) = 9.8 N

Question 4.
The earth and the moon are attracted to each other by gravitational force. Does the earth attract the moon with a force that is greater or smaller or the same as the force with which the moon attracts the earth? Why?
Answer:
According to the universal law of gravitation, two objects attract each other with equal force, but in opposite directions. The Earth attracts the moon with an equal force with which the moon attracts the earth.

Question 5.
If the moon attracts the earth, why does the earth not move towards the moon?
Answer:
The Earth and the moon experience equal gravitational forces from each other. However, the mass of the Earth is much larger than the mass of the moon. Hence, it accelerates at a rate lesser than the acceleration rate of the moon towards the Earth. For this reason, the Earth does not move towards the moon

Question 6.
What happens to the force between two objects, if
(i) the mass of one object is doubled?
(ii) the distance between the objects is doubled and tripled?
(iii) the masses of both objects are doubled?
Answer:
(i) Doubled
(ii) One-fourth and one-ninth
(iii) four times
According to the universal law of gravitation, the force of gravitation between two objects is given by:
F = \(\frac{\mathrm{G} m_{1} m_{2}}{r^{2}}\)
(i) F is directly proportional to the masses of the objects. If the mass of one object is doubled, then the gravitational force will also get doubled.

(ii) F is inversely proportional to the square of the distances between the objects. If the distance is doubled, then the gravitational force becomes one-fourth of its original value.
Similarly, if the distance is tripled, then the gravitational force becomes one-ninth of its original value.

(iii) F is directly proportional to the product of masses of the objects. If the masses of both the objects are doubled, then the gravitational force becomes four times the original value.

Question 7.
What is the importance of universal law of gravitation?
Answer:
The universal law of gravitation proves that every object in the universe attracts every other object.

Question 8.
What is the acceleration of free fall?
Answer:
When objects fall towards the Earth under the effect of gravitational force alone, then they are said to be in free fall. Acceleration of free fall is 9.8 ms^-2, which is constant for all objects (irrespective of their masses).

Question 9.
What do we call the gravitational force between the Earth and an object?
Answer:
Gravitational force between the earth and an object is known as the weight of the object.

Question 10.
Amit buys few grams of gold at the poles as per the instruction of one of his friends. He hands over the same when he meets him at the equator. Will the friend agree with the weight of gold bought? If not, why? [Hint: The value of g is greater at the poles than at the equator].
Answer:
Weight of a body on the Earth is given by:
W = mg
Where,
m = Mass of the body
g = Acceleration due to gravity

The value of g is greater at poles than at the equator. Therefore, gold at the equator weighs less than at the poles. Hence, Amit’s friend will not agree with the weight of the gold bought.

Question 11.
Why will a sheet of paper fall slower than one that is crumpled into a ball?
Answer:
When a sheet of paper is crumbled into a ball, then its density increases. Hence, resistance to its motion through the air decreases and it falls faster than the sheet of paper.

Question 12.
Gravitational force on the surface of the moon is only \(\frac {1}{5}\) as strong as gravitational force on the Earth. What is the weight in newtons of a 10 kg object on the moon and on the Earth?
Answer:
Weight of an object on the moon = \(\frac {1}{6}\) × Weight of an object on the Earth
Also,
Weight = Mass × Acceleration
Acceleration due to gravity, g = 9.8 m/s²
Therefore, weight of a 10 kg object on the Earth = 10 × 9.8 = 98N
And, weight of the same object on the moon = \(\frac {1}{6}\) × 98 = 16.3 N

Question 13.
A ball is thrown vertically upwards with a velocity of 49 m/s. Calculate
(i) the maximum height to which it rises.
(ii) the total time it takes to return to the surface of the earth.
Answer:
(i) 122.5 m (ii) 10 s
According to the equation of motion under gravity: v² – u² = 2 gs
Where,
u = Initial velocity of the ball
v = Final velocity of the ball
s = Height achieved by the ball
g = Acceleration due to gravity
At maximum height, final velocity of the ball is zero, i.e., v = 0
u = 49 m/s
During upward motion, g = – 9.8 m s^-2
Let h be the maximum height attained by the ball.
Hence,
0-(49)² = 2 × (-9.8) × h
h = \(\frac{49 \times 49}{2 \times 9.8}\) = 122.5 m
Let t be the time taken by the ball to reach the height 122.5 m, then according to the equation of motion:
v = u + gt
We get,
0 = 49 + t × (-9.8)
9.8t = 49
t = \(\frac{49}{9.8}\) = 5s
But,
Time of ascent = Time of descent
Therefore, total time taken by the ball to return = 5 + 5 = 10 s

Question 14.
A stone is released from the top of a tower of height 19.6 m. Calculate its final velocity just before touching the ground.
Answer:
According to the equation of motion under gravity:
v₂ – u₂ = 2 gs
Where,
u = Initial, velocity of the stone = 0
v = Final velocity of the stone
s = Height of the stone = 19.6 m
g = Acceleration due to gravity = 9.8 m s^-2
∴ v₂ – 0₂ = 2 × 9.8 × 19.6
v₂ = 2 × 9.8 × 19.6 = (19.6)²
v = 19.6 ms^-1
Hence, the velocity of the stone just before touching the ground is 19.6 m s^-1.

Question 15.
A stone is thrown vertically upward with an initial velocity of 40 m/s. Taking g = 10 m/s², find the maximum height reached by the stone. What is the net displacement and the total distance covered by the stone?
Answer:
According to the equation of motion under gravity:
v₂ -u₂ = 2 gs
Where,
u = Initial velocity of the stone = 40 m/s
v = Final velocity of the stone = 0
s = Height of the stone
g = Acceleration due to gravity = -10 m s^-2
Let h be the maximum height attained by the stone.

Therefore,
0 – (40)2 = 2 × h × (-10).
h = \(\frac{40 \times 40}{20}\) = 80 m
Therefore, total distance covered by the stone during its upward and downward journey = 80 + 80 = 160 m
Net displacement of the stone during its upward and downward journey = 80 + (-80) = 0

Question 16.
Calculate the force of gravitation between the earth and the Sun, given that the mass of the earth = 6 × 10²⁴ kg and of the Sun = 2 × 10³⁰ kg. The average distance between the two is 1.5 × 10¹¹ m.
Answer:
According to the universal law of gravitation, the force of attraction between the Earth and the Sim is given by:
F = \(\frac{\mathrm{GM}_{\text {Sun }} \mathrm{M}_{\text {Earth }}}{\mathrm{R}^{2}}\)
Where,
MSun = Mass of the Sun = 2 × 10³⁰ kg
MEarth = Mass of the Earth = 6 × 10²⁴ kg
R = Average distance between the Earth and the Sun = 1.5 × 10¹¹ m
G = Universal gravitational constant = 6.7 × 10^-11 Nm² kg^-2
F = \(\frac{6.7 \times 10^{-11} \times 2 \times 10^{36} \times 6 \times 10^{24}}{\left(1.5 \times 10^{11}\right)^{2}}\) = 3.57 × 10²² N

Question 17.
A stone is allowed to fall from the top of a tower 100 m high and at the same time another stone is projected vertically upwards from the ground with a velocity of 25 m/s. Calculate when and where the two stones will meet.
Answer:
Let the two stones meet after a time t.
For the stone dropped from the tower:
Initial velocity, u = 0
Let the displacement of the stone in time t from the top of the tower be s.
Acceleration due to gravity, g = 9.8 m s^-2
From the equation of motion,
S = ut + \(\frac {1}{2}\)gt²
= 0 × t + \(\frac {1}{2}\) × 9.8 × t² ………. (i)

(ii) For the stone thrown upwards:
Initial velocity, u = 25 m s^-1
Let the displacement of the stone from the ground in time t be s’.
Acceleration due to gravity, g = -9.8 ms^-2
Equation of motion,
s’ = ut + \(\frac {1}{2}\)gt²
= 25f – \(\frac {1}{2}\) × 9.8t²
∴ s’ = 25t – 9t² ………. (2)
The combined displacement of both the stones at the meeting point is equal to the height of the tower 100 m.
∴ s + s’ = 100
\(\frac {1}{2}\)gt² + 25t – \(\frac {1}{2}\)gt² = 100
∴ t = \(\frac {100}{25}\) = 4 s
In 4 s, the falling stone has covered a distance given by equation (1) as
s = \(\frac {1}{2}\) × 10 × 4² = 80m
Therefore, the stones will meet after 4 s at a height (100 – 80) = 20 m from the ground

Question 18.
A ball thrown up vertically returns to the thrower after 6 s. Find
(a) the velocity with which it was thrown up,
(b) the maximum height it reaches, and
(c) its position after 4 s.
Answer:
(a) 29.4m/s
(b) 44.1 m
(c) 39.2 m above the ground

(a) Time of ascent is equal to the time of descent The ball takes a total of 6 s for its upward and downward journey.
Hence, it has taken 3 s to attain the maximum height.
Final velocity of the ball at the maximum height, v = 0
Acceleration due to gravity, g = -9.8 ms^-2
Equation of motion, v = u + gt will give,
0 = u + (-9.8 × 3)
u = 9.8 × 3 = 29.4 ms^-1
Hence, the ball was thrown upwards with a velocity of 29.4 ms^-1.

(b) Let the maximum height attained by the ball be h.
Initial velocity during the upward journey, u = 29.4 ms^-1
Final velocity, v = 0
Acceleration due to gravity, g = -9.8 ms^-2
From the equation of motion, s = ut + \(\frac {1}{2}\)at²
h = 29.4 × 3+ \(\frac {1}{2}\) × -9.8 × (3)² = 44.1m

(c) Ball attains the maximum height after 3 s. After attaining this height, it will start falling downwards.
In this case,
Initial velocity, u = 0
Position of the ball after 4 s of the throw is given by the distance travelled by it during its downward journey in 4s -3s = 1s.
Equation of motion, s = ut + \(\frac {1}{2}\)gt² will give,
s = 0 × t + \(\frac {1}{2}\) × 9.8 × 1² = 4.9 m
Total height = 44.1 m
This means that the ball is 39.2 m (44.1 m – 4.9 m) above the ground after 4 seconds.

Question 19.
In what direction does the buoyant force on an object immersed in a liquid act?
Answer:
An object immersed in a liquid experiences buoyant force in the upward direction.

Question 20.
Why does a block of plastic released under water come up to the surface of water?
Answer:
Two forces act on an object immersed in water. One is the gravitational force, which pulls the object downwards, and the other is the buoyant force, which pushes the object upwards. If the upward buoyant force is greater than the downward gravitational force, then the object comes up to the surface of the water as soon as it is released within water. Due to this reason, a block of plastic released under water comes up to the surface of the water.

Question 21.
The volume of 50 g of a substance is 20 cm³. If the density of water is 1 g cm^-3, will the substance float or sink?
Answer:
If the density of an object is more than the density of a liquid, then it sinks in the liquid. On the other hand, if the density of an object is less than the density of a liquid, then it floats on the surface of the liquid.
Here, density of the substance = \(\frac{\text { Mass of the substance }}{\text { Volume of the substance }}=\frac{50}{20} 2.5 \mathrm{~g} \mathrm{~cm}^{-3}\)
The density of the substance is more than the density of water (1 g cm^-3). Hence, the substance will sink in water.

Question 22.
The volume of a 500 g sealed packet is 350 cm³. Will the packet float or sink in water if the density of water is 1 g cm^-3? What will be the mass of the water displaced by this packet?
Answer:
Density of the 500 g sealed packet
\(\frac{\text { Mass of the packet }}{\text { Volume of the packet }}=\frac{500}{350}=1.428 \mathrm{gcm}^{-3} \)
The density of the substance is more than the density of water (1 g cm^-3). Hence, it will sink in water.
The mass of water displaced by the packet is equal to the volume of the packet, i.e., 350 g.

Class 9 Science Chapter 10 Gravitation Additional Important Questions and Answers

Multiple Choice Questions
Choose the correct option:

Question 1.
Two objects of different masses falling freely near the surface of moon would
(a) have same velocities at any instant
(b) have different accelerations
(c) experience forces of same magnitude
(d) undergo a change in their inertia
Answer:
(a) have same velocities at any instant

Question 2.
The value of acceleration due to gravity
(a) is same on equator and poles
(b) is least on poles
(c) is least on equator
(d) increases from pole to equator
Answer:
(c) is least on equator

Question 3.
The gravitational force between two objects is F. If masses of both objects are halved without changing distance between them, then the gravitational force would become
(a) F/4
(b) F/2
(c) F
(d) 2F
Answer:
(a) F/4

Question 4.
A boy is whirling a stone tied with a string in an horizontal circular path. If the string breaks, the stone
(a) will continue to move in the circular path
(b) will move along a straight line towards the centre of the circular path
(c) will move along a straight line tangential to the circular path
(d) will move along a straight line perpendicular to the circular path away from the boy
Answer:
(c) will move along a straight line tangential to the circular path

Question 5.
An object is put one by one in three liquids having different densities. The object floats with 1/9, 2/11, 3/7, and parts of their volumes outside the liquid surface in liquids of densities d₁, d₂ and d₃ respectively. Which of the following statement is correct?
(a) d₁ > d₂ > d₃
(b) d₁ > d₂ < d₃
(c) d₁ < d₂ > d₃
(d) d₁ < d₂ < d₃
Answer:
(d) d₁ < d₂ < d₃

Question 6.
In the relation F = GMm/d2, the quantity G
(a) depends on the value of g at the place of observation
(b) is used only when the earth is one of the two masses
(c) is greatest at the surface of the earth
(d) is universal constant of nature
Answer:
(d) is universal constant of nature

Question 7.
Law of gravitation gives the gravitational force between
(a) the earth and a point mass only
(b) the earth and Sim only
(c) any two bodies having some mass
(d) two charged bodies only
Answer:
(c) any two bodies having some mass

Question 8.
The value of quantity G in the law of gravitation
(a) depends on mass of earth only
(b) depends on radius of earth only
(c) depends on both mass and radius of earth
(d) is independent of mass and radius of the earth
Answer:
(d) is independent of mass and radius of the earth

Question 9.
Two particles are placed at some distance. If the mass of each of the two particles is doubled, keeping the distance between them unchanged, the value of gravitational force between them will be
(a) 1/4 times
(b) 4 times
(c) 1/2 times
(d) unchanged
Answer:
(b) 4 times

Question 10.
The atmosphere is held to the earth by
(a) gravity
(b) wind
(c) clouds
(d) earth’s magnetic field
Answer:
(a) gravity

Question 11.
The force of attraction between two unit point masses separated by a unit distance is called
(a) gravitational potential
(b) acceleration due to gravity
(c) gravitational field
(d) universal gravitational constant
Answer:
(d) universal gravitational constant

Question 12.
The weight of an object at the centre of the earth of radius R is
(a) zero
(b) infinite
(c) R times die weight at the surface of the earth
(d) 1/R₂ times the weight at surface of the earth
Answer:
(a) zero

Question 13.
An object weighs 10 N in air. When immersed fully in water, it weighs only 8 N. The weight of the liquid displaced by the object will be
(a) 2 N
(b) 8 N
(c) 10 N
(d) 12 N
Answer:
(a) 2 N

Question 14.
A girl stands on a box having 60 cm length, 40 cm breadth and 20 cm width in three ways. In which of the following cases, pressure exerted by the brick will be
(a) maximum when length and breadth form the base
(b) maximum when breadth and width form the base
(c) maximum when width and length form the base
(d) the same in all the above three cases
Answer:
(b) maximum when breadth and width form the base

Very Short Answer Type Questions

Question 1.
State what causes the revolution of planets around the sun?
Answer:
Gravitational force of attraction between the sun and planets.

Question 2.
What is the direction of gravitation force acting between the two objects?
Answer:
The force of gravitation between two objects act along the line joining their centres of mass.

Question 3.
How does the gravitation force of attraction vary with the distance between them?
Answer:
The gravitation force of attraction is universely proportional to the square of distance between die centres of their mass.

Question 4.
State the effect on the gravitational force of attraction between two objects
(i) When distance is halved
(ii) When distance is doubled
Answer:
(i) When distance is halved, the force increases by four times.
(ii) When distance is doubled, the force decreases by four times.

Question 5.
How does the gravitation force of attraction between two objects depend upon their masses?
Answer:
The force of gravitation is directly proportional to the product of the masses of two objects.
F ∝ m₁.m₂

Question 6.
If the mass of a body is doubled and that of another body is tripled, what would be the effect of gravitational force?
Answer:
The gravitational force would increase by six times.

Question 7.
State any one physical quantity that does not affect the magnitude of acceleration due to gravity.
Answer:
MaSs of the body.

Question 8.
What is the magnitude of universal gravitational constant?
Answer:
6.67 × 10^-11 Nm²kg^-2.

Question 9.
Does the value of universal gravitational constant change in universe?
Answer:
No, its a constant value.

Question 10.
What is the Value of ‘g’ acceleration due to gravity on moon?
Answer:
The value of acceleration due to gravity on moon surface is 1/6 th of value of acceleration of gravity on earth i.e. 1.63 ms^-2.

Question 11.
If a body of mass ‘m’ revolves in a circle of radius ‘r’, then what would be the magnitude of the acceleration produced in the body?
Answer:
The magnitude of acceleration produced (a) = \(\frac{v^{2}}{r}\)

Question 12.
What is the relation between ‘g’ and ‘G’?
Answer:
g = \(\frac{\mathrm{GM}}{\mathrm{R}^{2}}\)
When M is mass of earth and R is the radius of earth.

Question 13.
Why do the nails and pins have pointed ends?
Answer:
The nails and pins have pointed ends to reduce area and increase the effect of applied force i.e. pressure.

Question 14.
What is the S.I. unit of density and relative density?
Answer:
Relative density has no unit but for density S.I. unit kg/m³.

Question 15.
State the principle that describes the working of hydrometer or lactometer.
Answer:
Archimedes principle.

Question 16.
What is lactometer?
Answer:
It is a device used to measure the purity of milk i.e. amount of water present in milk.

Question 17.
What is hydrometer?
Answer:
It is a device used to measure the density of a liquid.

Question 18.
State Archimedes principle.
Answer:
The principle states that when an object is immersed in fluid partially or completely, it experiences an upward thrust that is equal to the weight of the fluid displaced by it.

Question 19.
Where will a student find the mass of 1kg heavier, when weighted in air or in water? Why?
Answer:
In air because the buoyant force in air is less than in water.

Question 20.
If a student drops a feather and an iron block in vacuum from a particular height. Which of the two will land first? Why?
Answer:
Both feather and iron block would land at the same time because acceleration due gravity is independent of mass.

Short Answer Questions

Question 1.
What do you understand by gravitation and gravity?
Answer:
Gravitation refers to the force with which any two objects in universe attract each other irrespective of their masses and distance between them. Gravity refers to force with which earth attracts an object towards its centre.

Question 2.
Does earth attracts moon towards itself? If yes, why does the moon then not fall on the earth?
Answer:
Earth and moon have gravitational force that acts in between them. Moon revolving round the earth undergoes a change in its acceleration because of changing direction. Moreover, the motion of moon around earth is because of centripetal gravitational force which is balanced by moon’s centrifugal gravitational force to prevent it’s falling down on the earth.

Question 3.
It is seen that an apple is attracted towards the earth. Does the apple attract the earth? If yes, why does the earth not move towards the apple?
Answer:
According to universal law of gravitation apple also attracts the earth with the same force as the earth attracts the apple but in opposite direction.
Force acting on the apple due to earth’s attraction, F = mg.
Apple also attracts the earth with same force. Therefore, acceleration produced on the earth
(a) = \(\frac{\mathrm{F}}{\mathrm{M}_{\mathrm{e}}}=\frac{m g}{\mathrm{M}_{e}}\)

However, the mass of earth is 6.0 × 10²⁴ kg which is very large as compared to the mass of an apple. Therefore, the value of acceleration produced in the earth is very-very small or negligible for the earth to show any visible movement towards the apple.

Question 4.
State the factors which affect the gravitation force of attraction in between two objects?
Answer:
There are two factors which affect the force of attraction between two objects. These factors include:

1. Mass, because the force of gravitation is directly proportional to the product of the masses of two bodies.
2. Distance between the two bodies because of the force of attraction is inversely proportional to the square of the distance in between them.

Question 5.
What is gravitational constant ‘G’ ? What is its S.I. unit?
Answer:
The gravitational force of attraction between two bodies/objects is given by
F = \(\mathrm{G} \frac{m_{1} m_{2}}{d^{2}}\)
Where ‘G’ is universal gravitational constant.
G = \(\frac{\mathrm{F} d^{2}}{m_{1} m_{2}}\)
Putting the S.I. units of different physical quantities.
G = \(\frac{\mathrm{N} m^{2}}{\mathrm{~kg} . \mathrm{kg}}\) = nm²kg^-2
Hence, S.I. units of G is Mm² kg^-2.

Question 6.
What do you understand by acceleration due to gravity? Does it depend upon the mass?
Answer:
It refers to the acceleration gained by a free falling body towards the earth. It is represented by symbol ‘g’ and its value is 9.8 m/s² i.e. a free falling body gains an acceleration of 9.8 m/s² every second during tire course of its fall.
It does not depend upon the mass of the object.

Question 7.
What is the difference between ‘g’ and ‘G’ ?
Answer:

g	G
1. It represents acceleration produced in free, falling body due to gravitational force.	1. It represents universal gravitational constant.
2. It’s value is 9.8 ms-2	2. It’s value is 6.67 × 10-11 Mm2 kg-2
3. It’s value is not fixed but changes from place to place.	3. It’s value is a fixed value.

Question 8.
Calculate the value of ‘g’ on the surface of earth.
Answer:
We know that g = \(\frac{\mathrm{GM}}{\mathrm{R}^{2}}\)
M, mass of earth = 6.0 × 10²⁴ kg
R1 radius of earth = 6.4 × 10⁶ m.
G, Gravitational constant = 6.67 × 10^-11 Nm² kg^-2
g = \(\frac{6.67 \times 10^{-11} \mathrm{Nm} \mathrm{kg}^{-2} \times 6.0 \times 10^{24} \mathrm{~kg}}{\left(6.4 \times 10^{6}\right)^{2} \mathrm{~m}}\)
= \(\frac{400.38}{40.96}=9.8 \mathrm{~ms}^{-2}\)

Question 9.
What will happen to the weight of a body when it is taken down inside the earth?
Answer:
The weight of the body decreases because the effective mass of the earth with which it attracts the body towards it centre decreases. The decrease in weight due to decresing effecting mass of the earth overpowers the increase in weight due to decrease in distance.

Question 10.
Define mass and weight. What are their S.I. units?
Answer:
Mass is defined as the quantity of matter contained in a body that remains unchanged throughout the universe. It’s S.I. units is kilograms. Weight is defined as the force with which the earth attracts the object towards its centre.
Weight (W) = m × g
where m = mass of body
g = accelertion due to gravity
The S.I. unit of weight is Netwon(N).

Question 11.
Where do you expect the weight of a body to be more, at poles or at equator? Why?
Answer:
The earth is not a perfect spherical structure. It is compressed at poles therefore the radius of earth is greater at equator than at poles. With value of ‘g’ inversely proportional to square of distance from the centre of earth, the value of ‘g’ is comparitively more at poles than at equator. Therefore, the weight of an object is maximum at poles and minimum at equator.

Question 12.
Write the equation of motion for free falling bodies due to gravitational force of attraction on earth.
Answer:
When u = initial velocity, v = final velocity,
g = acceleration due to gravity, s = distance covered and time = t, then
V = u + gt
s = ut + \(\frac {1}{2}\)gt²
2gs = v² – u²

Question 13.
According to Cartesian convention what are the sign for acceleration due to gravity ‘g’. Velocity ‘v’ and distance covered ‘s’ ?
Answer:
(i) According to cartesian convention ‘g’ is always taken in negative since its acts in downward direction. It is always taken in negative whether a body goes up or comes down.

(ii) The value of velocity V is taken in positive when a body goes in upward direction and when it come down, it value is taken in negative. (Fig. 10.2)
(iii) Distance is also taken in positive when a body goes up and taken in negative when falls down on the earth.

Question 14.
What is thrust and pressure? How are they different?
Answer:

Thrust	Pressure
1. It is the force that acts on an object perpendicular to its surface.	It is the thrust acting per unit area of a surface.
2. It S.I. unit is Newton (N).	It’s unit is Netwon per metre square (N/m2)

Question 15.
Why cutting tools like pair of scissors, knives or axes have sharp edges?
Answer:
The edges of pair of scissors, knives and axes are made sharp to increase the effect of the applied force on them. The pressure is universely proportional to area i.e. with the decreasing area, pressure increases.

Question 16.
What is bouyant force? How will you determine the bouyant force?
Answer:
Bouyant force is an upward force that is exerted on a body when it is partially or fully immersed in a liquid like water. However, the magnitude of bouyant force depends upon the density of liquid, with increasing density of fluid, the bouyant force also increases.

The magnitude of the force of bouyancy is determined by measuring the weight of the fluid displaced by the object when immersed in a liquid.

Question 17.
Does a body experience the same bouyant force in different fluids? If not, why?
Answer:
A body immersed in different fluids such as water, alcohol and cooking oil will experience different bouyant force because the bouyant force exerted on a body immersed in a fluid depends upon, the fluid’s density. The bouyant force increases with increasing density of the fluid.

Question 18.
What is law of floatation?
Answer:
The law of floatation describes, the conditions in which a body would float or sink. When immersed in a liquid, the law states that:

• If relative density of a body is more than one, it would sink in the water.
• If relative density is less than one, it will float on water.

Question 19.
Why a nail or a rupee coin sinks in water but a ship floats in water?
Answer:
The weight of water displaced by a nail or a rupee coin is less than the weight of the nail or rupee coin. Therefore, with less upward thrust applied on them, they sink in water.

A ship being large is so designed that the water displaced by the ship is more than the weight of the ship i.e. upward thrust is more on ship to keep it floating in water.

Question 20.
What do you understand by density and the relative density? What are their S.I. units?
Answer:
Density refers to the mass per unit volume of a substance.
Mass of substance = \(\frac{\text { Mass of substance }}{\text { Volume of substance }}\)
It’s S.I. unis is kg/m³.
Relative density refers to the ratio of the density of a substance to the density of pure water.
Relative density = \(\frac{\text { Density of substance }}{\text { Density of water }}\)
Relative density being a ratio has no unit.

Question 21.
What is the force of gravitation in between two boys having mass equal to 50 kg and 40 kg respectively and separated by a distance of lm from each other?
Answer:
Mass of one boy m₁ = 50 kg, Mass of other boy, m₂ = 40 kg Distance between them, d = 1m.
Value of G = 6.67 × 10^-1 Nm² kg^-2
According to law of gravitation, force of attraction between them is given by
F = G \(\frac{m_{1} m_{2}}{d^{2}}\)
= \(\frac{6.67 \times 10^{-11} \times 50 \times 40}{(1)^{2}}\)
= 1.334 × 10^-7 N

Question 22.
Calculate the force exerted by earth on the moon. If the mass of the earth 6.0 × 10²⁴ kg and that of the moon is 7.4 × 10²² kg. The distance between the earth and the moon is 3.84 × 10^-11. (G = 6.67 × 10^-11 Nm² kg^-2).
Answer:
Mass of the earth, M = 6.0 × 10²⁴ kg.
Mass of the moon, m = 7.4 × 10²² kg.
The distance between moon and earth, r = 3.84 × 10²⁴ m.
The force exerted by earth on moon is given by

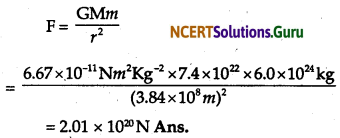
Question 23.
A car falls off a ledge and drops in % seconds. Let g = -10 ms^-2.
(i) What will be its speed on striking the ground?
(ii) What is its average speed during the % second?
(iii) How high is the ledge from the ground.
Answer:
Given: Initial velocity of car = 0 ms^-1
Acceleration due to gravity, g = -10 ms^-2
lime taken, t = 1/2 second.
(i) Let speed on striking the groun d,v = ?
v = u + gt
= 0 – 10 × \(\frac {1}{2}\) = -5 ms^-1
Negative sign indicates that car is moving downward.

(ii) Average speed of the car
\(\frac{u+v}{2}=\frac{0+(-5)}{2}=2.5 \mathrm{~ms}^{-1}\)
Average speed is 2.5 ms^-1 downward.

(iii) Let the height of ledge from the ground
h = ut + \(\frac {1}{2}\)gt²
= 0 × \(\frac {1}{2}\) + \(\frac {1}{2}\) (-10)(\(\frac {1}{2}\))2
= \(-\frac{5}{4}\) = -1.25 m.
The distance travelled has a negative sign this means that the car is moving in downward direction.

Question 24.
A stone is dropped from 180 m high tower. How long does the stone tak to reach the ground ? What is the velocity when it touches the ground ? (Take g = -10 ms^-2)
Answer:
Height of the tower, h = – 180m
Initial velocity, u = 0
Let time taken to reach the ground, t = ?
Let velocity with which it touches the ground, v = ?
We know that
h = ut + \(\frac {1}{2}\)gt²
-180 = 0 × t + \(\frac {1}{2}\) (-10)t²
180 = 5t²
t2 = \(\frac {180}{5}\) = 36 or t = 6
(ii) u = u+gt = 0 – 15 × 6
= -60 m/s
Negative sign indicates that the body is moving in downward direction.

Question 25.
A body is thrown vertically upward rises to a height of 10m. Calculate.
(i) The velocity with which body was thrown upward.
(ii) The time taken by the body to reach the highest point.
Answer:
(i) Maximum height reached by the body, h = 10m.
Let initial velocity =?
Final velocity, v =0
Acceleration due to gravity g = – 9.8 ms^-2
We know that v² – u² = 2 (-9.8) × 10
u² = 196
u = \(\sqrt{196}\) = 14ms^-1

(ii) Initial velocity of the body = 14 ms^-1
v = u + gt
0 = 14 – 9.8 × t
t = \(\frac {14}{9.8}\) = 1.43 second
Time taken by the body to reach maximum height = 1.43 s.

Question 26.
The mass of an object is 50 kg on earth. What is its weight on the earth and what will be its weight on the moon?
Answer:
Mass of the object = 50 kg.
Acceleration due to gravity at earth, g = 9.8 ms^-2
Weight on earth = m × g = 50 × 9.8 = 490 N
Acceleration due to gravity, g on moon = \(\frac{9.8}{6} m \mathrm{~s}^{-2}\)
Weight on moon = m × g
= \(\frac{50 \times 9.8}{6}\) = 81.67 N

Question 27.
Find the mass of an object whose weight on the earth is 49 N. What is its mass on the surface of moon?
Answer:
Weight on the earth, W = 49 N.
Acceleration due to gravity on earth, g = 9.8 ms^-2.
We know that W = m.g.
m = \(\frac{W}{g}=\frac{49}{9.8}\) = 5 kg.
Mass of the body on earth = 5 kg.
Mass of the body on moon = 5 kg
(Because the mass remains constant at every place).

Question 28.
Calculate the mass of the moon. If the radius of the moon ‘R_m‘ is 1.60 × 10⁶ m. The acceleration due to gravity at moon is 1/6th of the gravity at earth.
Answer:
Let mass of the moon = M_m
Mass of the earth = m_e
We know that acceleration due to gravity ‘g’ at each is given by g = \(\frac{\mathrm{GM}_{e}}{\mathrm{R}_{\mathrm{e}}{ }^{2}}\)
Similarly, gravity at moon, g will be given by

Question 29.
A block of wood is a kept on tabletop. The mass of the wooden block is 5kg and its dimension are 40 cm × 20 cm × 10cm. Find the pressure exerted by the wooden block on the tabletop if it is made to lie on the tabletop with its side& of dimension (i) 20m × 10cm. (ii) 40 cm × 20 cm.
Answer:
The mass of the wooden block = 5 kg.
The force exerted by wooden block = mg = 5 × 9.8 = 49 N
(i) When wooden block lie with its 20 cm × 10 cm side on the tabletop.
Area of block in contact with table top = 20 × 10 = 200 cm² = 0.02 m²
Force = \(\frac{\text { Force }}{\text { Area }}=\frac{49}{0.02}\) = 2450 Nm²

(ii) When wooden block lie with its side 40 × 20 cm on the table top:
Area in contact with table = 40 × 20 = 800 cm² = 0.08 m².
Pressure = \(\frac{\text { Force }}{\text { Area }}=\frac{49}{0.08}\) = 612.5 Nm^-2.

Question 31.
The relative density of silver is 10.8. The density of water is 1 kg m^-3. What is the density of silver?
Answer:
Relative density of silver = 10.8 kgm^-3
Density of water = 10³kg m^-3
Relative density = \(\frac{\text { Density of silver }}{\text { Density of water }}\)
Density of silver = Relative density × Density of water
= 10.8 × 10³ kgm^-3

Question 32.
A cubical block of mass 5 kg with each side 5 cm is lying on a table top. Calculate the pressure exerted by the block.
Answer:
Mass of the block = 5 kg
Thrust exerted by the block =m × g
= 5 × 9.8 = 49.0 N
Side of cubical block = 5 cm = 0.05 m
Area of the surface in contact with table top
= (0.05)² = 0.0025 m² = 2.5 × 10^-3 m²
Pressure exerted = \(\frac{\text { Thrust }}{\text { Area }}\)
= \(\frac{49.0}{2.5 \times 10^{-3}}\) = 1.86 × 10⁴ Nm^-2 or Pa.

Long Answer Questions

Question 1.
State the Kepler’s laws that describe the motion of the planets around the earth.
Answer:
The motion of the planets are governed by the following Kepler’s laws.
(i) The orbit of a planet is elliptical with the Sun at one of the focus, as shown in the figure 10.3.
(ii) The line joining the planet and the sun sweeps equal area in equal intervals of time. Thus, in the given figure if the time of interval of moving from A to B is the same as that from C to D, then the area OAB and OCD are equal.

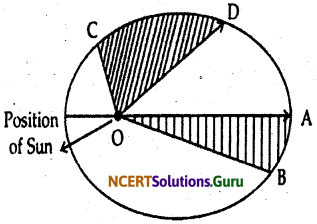
(iii) The cube of the mean distance of a planet from the Sun is proportional to the square of its orbital period, i.e. time taken by the planet to complete its orbit T:
r³ ∝ T²
or \(\frac{r^{3}}{\mathrm{~T}^{2}}\) = constant
where r = Mean distance of the planet from sun.
T = Orbital period.

Question 2.
What is inverse square rule? How did Newton guess or arrived the inverse square rule?
Answer:
Inverse square rule: When a planet revolves around the sun, the force of attraciton between sun and planet is inversely proportional to the square of radius of the orbit.
F ∝ \(\frac{1}{r^{2}}\)
F = Force of attraction between sun and planet.
r = Radius of the orbit of a planet.

Newton showed that the cause of planetary motion is the gravitational force of attraction that sun exert on planets. Newton used the third law of Kepler to guess the inverse square rule.

Suppose a planet is moving in an orbit. We can assume Planetary orbits as circular orbit. Let the radius of the circular orbit is ‘r’ and planet is moving with a linear velocity ‘v’.
Then, the force ‘F’ acting on the planet of mass ‘m’ is given by
F = \(\frac{m v^{2}}{r}\)
or F ∝ \(\frac{v 2}{\bar{r}}\) ………(i)
(m = mass of planet is contant)
If let T is the taken by the planet to complete one orbit, then,

Therefore, we have, v² ∝ \(\frac{1}{r}\)
combining (i) and (ii) we have
F ∝ \(\frac{1}{r^{2}}\)

Question 3.
What do you mean by acceleration due to gravity? How will you prove that acceleration due to gravity is independent of the mass and nature of the body?
Answer:
Acceleration due to gravity: When body falls freely due to the gravitational force of attraction of the earth, there is no change in its direction of motion but its velocity changes by equal amounts in each second. So the acceleration produced in the body due to earth’s gravitation force of attraction is known as the acceleration due to gravity. It is denoted by.

Let a body of mass ‘m’ is falling downward due to force of gravity and acceleration produced in the body is ‘g’. Then according the Newton’s second law of motion, gravitation force acting on the body is given by
F = mg ……..(i)
But the gravitation force of attraction between the body of mass ‘m’ and earth is given by
F = \(\frac{\mathrm{GM}_{m}}{d^{2}}\)
where M = mass of the earth
d = distance between the body and the centre of the earth from (i) and (ii)
mg = \(\frac{\mathrm{GM}_{m}}{d^{2}}\)
g = \(\frac{\mathrm{GM}}{d^{2}}\)
The expression of ‘g’ is independent of the mass of the object. Hence, acceleration due to gravity of the earth does not depend upon the mass and nature of the object.

Question 4.
Show that the weight of an object on the moon’s surface is 1/6th that of the earth.
Answer:
Let the mass of an object on moon’s surface is ‘m’.
Let weight of the object on moon’s surface = W
Let, Mass of moon =M
Radius of moon = R
Now the force of attraction by which moon attracts an object is equal to the weight of the object.
Therefore, Wm = \(\frac{\mathrm{GM}}{\mathrm{R}^{2}}\) ………(1)
Let the weight of the same object on earth = We
The force with which earth attracts the object is equal to the weight of the object on earth.
Therefore We = \(\frac{\mathrm{GM}_{\mathrm{e}} \mathrm{m}}{\mathrm{R}_{e}^{2}} \) ……..(2)
Where Me = mass of the earth and Re = Radius of earth.

But Mass of the earth is 100 times that of the moon and radius of the earth is 4 times the radius of moon.
Therefore, M_e = 100 M
and R_e = 4R
Putting these values in equation (2) we have
We = \(\frac{G(100 M) \times m}{(4 R)^{2}}\)
= \(\mathrm{G} \frac{100 \mathrm{Mm}}{16 \mathrm{R}^{2}}\) ……..(3)
Dividing equation (1) by (3)

or Weight on the moon = \(\frac {1}{6}\) × weight on the earth.

Question 5.
Show with the help of an activity that whenever a body is immersed in a liquid, it loses same weight due to force acting on the body in the upward direction (bouyant force).
Or
Show with the help of an activity that whenever an object is immersed in a fluid, a force acts on the object in upward direction.
Answer:
When an object is immersed in liquid, a force acts on the body in upward direction. ‘It can be shown by the following activity. (Fig. 10.4)

Activity: Take a piece of stone and tie it to one end of a spring balance. Suspend the stone by holding the string as shown in the figure. Note the extension produced in the reading in the spring balance due to the weight of the stone. Now, slowly dip the stone in water in a container.

As the stone is dipped in water, it loses the reading on spring balance scale. It continues declining till it gets completely immersed in water.

The decrease in extension of the spring shows that a force is acting on the stone in the upward direction. This upward thrust causes or brings a loss in the weight.

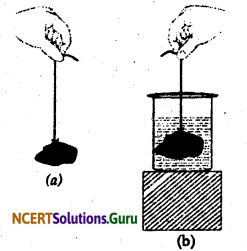
(a) Observe the elongation of the rubber string due to the weight of a piece of stone suspended form it in air.
(b) The elongation decreases as the stone, is immersed in water.

Question 6.
What is Archimedes principle? State some of its applications.
Answer:
Archimedes principle states that when an object is immersed in a fluid partially or fully, it experiences an upward thrust or force that is equal to the weight of the fluid displaced. The principle has helped.

• In designing ships and submarines.
• In designing lactometer to assess the purity of milk.
• In desgining hydrometer to measure the density of liquids.
• In assessing the purity of a given substance.