NCERT Solutions for Class 9 Maths Chapter 9 Areas of Parallelograms and Triangles Ex 9.4

These NCERT Solutions for Class 9 Maths Chapter 9 Areas of Parallelograms and Triangles Ex 9.4 Questions and Answers are prepared by our highly skilled subject experts.

NCERT Solutions for Class 9 Maths Chapter 9 Areas of Parallelograms and Triangles Exercise 9.4

Question 1.
Parallelogram ABCD and rectangle ABEF are on the same base AB and have equal areas. Show that the perimeter of the parallelogram is greater than that of the rectangle.
Solution:
Given: Parallelogram ABCD and rectangle ABEF with the same base AB and equal areas.

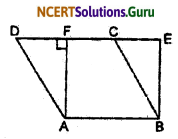
To prove that: Perimeter of ||gm ABCD > perimeter of rectangle ABEF.
i.e., AB + BC + CD + AD > AB + BE + EF + AF.
Proof: Since opposite sides of a ||gm and a rectangle are equal.
∴ AB = CD (Opposite sides of || gm)
and AB = EF (Opposit sides of rectangle)
∴ CD = EF
or AB + CD = AB + EF ……(i)
Now, we know that all the segments tlat can be drawn to a given line from a point not lying on it, the perpendicular segment is the shortest.
∴ BE < BC and AF < AD
∴ BC + AD > BE + AF ……(ii)
Adding (i) and (ii) we get
AB + CD + BC + AD > AB + EF + BE + AF
or, AB + BC + CD + AD > AB + BE + EF + AF
Therefore, the perimeter of || gm ABCD > perimeter of rectangle ABEF.

Question 2.
In Fig. 9.30, D and E are two points on BC such that BD = DE = EC. Show that ar (ABD) = ar (ADE) = ar (AEC). Can you now answer the question that you have left in the ‘Introduction’, of this chapter, whether the Held of Budhia has been actually divided into three parts of equal area?

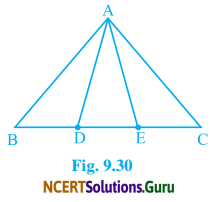
Solution:
Given: In ΔABC, D and E are two points on BC such that BD = DE = EC.
To prove that: ar (ΔABD) = ar (ΔADE) = ar (ΔAEC)
Construction: Draw AL ⊥ BC
Proof: In ΔADE
ar (ΔADE) = \(\frac {1}{2}\) × DE × AL ……(i)
ar (ΔABD) = \(\frac {1}{2}\) × BD × AL
or, ar (ΔABD) = \(\frac {1}{2}\) × DE × AL …(ii) (∵ BD = DE)
From equation (i) and (ii)
ar (ΔADE) = ar (ΔABD) …..(iii)
Again, ar (ΔAEC) = \(\frac {1}{2}\) × EC × AL
or, ar (ΔAEC) = \(\frac {1}{2}\) × DE × AL ……(iv) (∵ EC = DE given)
From equation (i) and (iv)
ar (ΔADE) = ar (ΔAEC) …..(v)
From equation (iii) and (v)
ar (ΔABD) = ar (ΔADE) = ar (ΔAEC)
Yes, Budhiya has used the result of this question in dividing her land into three equal parts.

Question 3.
In Fig. 9.31, ABCD, DCFE, and ABFE are parallelograms. Show that ar (ADE) = ar (BCF).

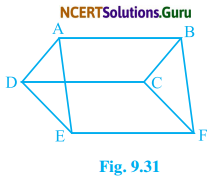
Solution:
In ΔADE and ΔBCF
AD = BC (Opposite sides of || gm ABCD)
DE = CF (Opposite sides of || gm DCFE)
and AE = BF (Opposite sides of || gm ABFE)
By S-S-S congruency condition.
ΔADE ≅ ΔBCF
We know that two congruent triangles have equal areas.
Therefore, ar (ΔADE) = ar (ΔBCF)

Question 4.
In Fig. 9.32, ABCD is a parallelogram, and BC is produced to a point Q such that AD = CQ. If AQ intersects DC at P, show that ar (BPC) = ar (DPQ).

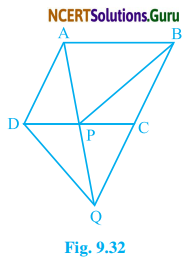
Solution:
Given: ABCD is a parallelogram in which side BC is produced to Q such that AD = CQ.
To prove that: ar (ΔBPC) = ar (ΔDPQ)
Construction: Join AC which intersects BP at O.
Proof: ΔBPC and ΔAPC lie on the same base PC and between the same parallel lines AB and CD.
∴ ar (ΔBPC) = ar (ΔAPC) ……(i)
(Δs on the same base and between same parallels are equal in the area)
Again, ΔCQD and ΔACQ lie on the same base CQ and between the same parallel lines AD and BQ.
∴ (ΔCQD) = ar (ΔACQ) …….(ii)
(As on the same base and between same parallels are equal in the area)
or, ar (ΔCQD) – ar (ΔCQP) = ar (ΔACQ) – ar (ΔCQP)
(Subtract ar (ΔCQP) both side)
ar (ΔDPQ) = ar (ΔAPC) ……(iii)
From equation (i) and (iii),
ar (ΔBPC) = ar (ΔDPQ)

Question 5.
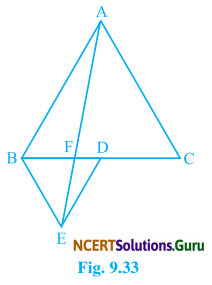
In Fig. 9.33, ABC and BDE are two equilateral triangles such that D is the midpoint of BC. If AE intersects BC at F, show that
(i) ar (BDE) = \(\frac {1}{4}\) ar (ABO)
(ii) ar (BDE) = \(\frac {1}{2}\) ar (BAE)
(iii) ar (ABC) = 2ar (BEC)
(iv) ar (BFE) = ar (AFD)
(v) ar (BFE) = 2ar (FED)
(vi) ar (FED) = \(\frac {1}{8}\) ar (AFC)

Solution:
Given: ABC and BED are two equilateral triangles. D is the midpoints of BC, and AE intersects BC at F.
To prove that:
(i) ar (BDE) = \(\frac {1}{4}\) ar (ABO)
(ii) ar (BDE) = \(\frac {1}{2}\) ar (BAE)
(iii) ar (ABC) = 2ar (BEC)
(iv) ar (BFE) = ar (AFD)
(v) ar (BFE) = 2ar (FED)
(vi) ar (FED) = \(\frac {1}{8}\) ar (AFC)

Construction: Join CE and AD and draw EG ⊥ BC and join.
Proof: ΔABC and ΔDEF both equilateral Δs.
∴ ∠ABC = ∠BDE (each 60°)
But it is the pair of alternate interior angle and we know that if pair of alternate interior angles are equal then the two lines are parallel.
∴ AB || DE
Similarly, AC || BE and AD || EF
(i) ar (ΔBDE) = \(\frac{\sqrt{3}}{4}\) (BD)²
(∵ Area of equilateral Δ = \(\frac{\sqrt{3}}{4}\) a²)
= \(\frac{\sqrt{3}}{4}\left(\frac{1}{2} \mathrm{BC}\right)^{2}\) (∵ D is mid point of BC)
\(\frac{\sqrt{3}}{4} \times \frac{1}{4} \mathrm{BC}^{2}\)
= \(\frac {1}{4}\) ar (ΔABC)
(∵ Area of equilateral Δ = \(\frac{\sqrt{3}}{4}\) a²)
So, ar (ΔBDE) = \(\frac {1}{4}\) ar (ΔABC)

(ii) ar(ΔBDE)= \(\frac {1}{2}\) ar(ΔBEC)
(∵ ED is the median of ΔEBC and median divide a Δ into two equal parts)
ΔBEC and ΔBAE lie on same base BE and between same parallels BE and AC.
∴ ar (ΔBEC) = ar (ΔBAE) ……(b)
(Δs on same base and between same parallels are equal in area)
From equation (a) and (b)
ar (ΔBDE) = \(\frac {1}{2}\) ar (ΔBAE)

(iii) We have
ar (ΔBEC) = ar (ΔBAE) ……(i)
(Prove above equ. (b))
Now, ΔBAE and ΔBAD lie on same base BA and between same parallels AB and DE.
∴ ar (ΔBAE) = ar (ΔBAD) ……(ii)
But ar (ΔBAD) = \(\frac {1}{2}\) ar (ΔABC) ……(iii)
(∵ median divides a triangle into two equal parts)
From equation (i), (ii) and (iii)
ar (ΔBEC) = \(\frac {1}{2}\) ar (ΔABC)
or, ar (ΔABC) = 2 ar (ΔBEC)

(iv) ΔBDE and ΔADE lie on same base DE and between same parallels DE and AB.
∴ ar (ΔBDE) = ar (ΔADE)
or, ar (ΔBDE) – ar (ΔDEF) = ar (ΔADE) – ar (ΔDEF)
[Subtract ar (ΔDEF) both side]
or, ar (ΔBFE) = ar (ΔAFD)

(v) In ΔABC and ΔDEB

Again, ΔDEB and ΔDEA lie on same base DE and between same parallels DE and AB.
∴ ar (ΔDEB) = ar (ΔDEA)
or, ar (ΔDEB) – ar (ΔDEA) = ar (ΔDEA) – ar (ΔDEF)
(Subtract ar (ΔDEF) both side)
or, ar (ΔBEF) = ar (ΔADF) ……(b)

(vi) We have given that
BC = 2BD = 2 (BF + FD) (∵ BD = BF + FD)
= 2 (2FD + FD) [From equation (c), BF = 2DF]
or, BC = 6FD ……(d)

Question 6.
Diagonals AC and BD of a quadrilateral ABCD intersect each other at P. Show that: ar (APB) × ar (CPD) = ar (APD) × ar (BPC)
Solution:
Given: ABCD is a quadrilateral in which diagonal, AC, and BD intersect each other at P.
To prove that: ar (APB) × ar (CPD) = ar (APD) × ar(BPC)

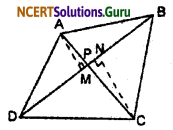
Construction: Draw, AM ⊥ BD, and CN ⊥ BD.
Proof: ar (ΔAPB) × ar (ΔCPD) = \(\frac {1}{2}\) × PB × AM × \(\frac {1}{2}\) × PD × CN
= \(\frac {1}{2}\) × PB × CN × \(\frac {1}{2}\) × PD × AM
= ar (ΔBPC) × ar (ΔAPD)
∴ ar (ΔAPB) × ar (ΔCPD) = ar (ΔAPD) × ar (ΔBPC)

Question 7.
P and Q are respectively the midpoints of sides AB and BC of a triangle ABC and R is the midpoint of AP. Show that
(i) ar (PRQ) = \(\frac {1}{2}\) ar (ARC)
(ii) ar (RQC) = \(\frac {3}{8}\) ar(ABC)
(iii) ar (PBQ) = ar (ARC)

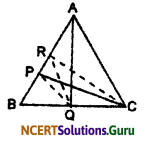
Solution:
Given: P and Q are the midpoint of the side AB and BC respectively and R is the midpoint of AP.
To prove that:
(i) ar (PRQ) = \(\frac {1}{2}\) ar (ARC)
(ii) ar (RQC) = \(\frac {3}{8}\) ar(ABC)
(iii) ar (PBQ) = ar (ARC)
Construction: Join AQ, CP, CR and PQ.
Proof: (i) In ΔAPC,
R is the mid point of AP.
So, ar (ΔARC) = ar (ΔPRC)
(Median divide a triangle into two equal parts)
or, ar (ΔARC) = \(\frac {1}{2}\) ar (ΔAPC) ……(i)
Now, ar (ΔAPC) = \(\frac {1}{2}\) ar (ΔABC) ……(ii)
(PC is the median of ΔABC)
and ar (ΔAQB) = \(\frac {1}{2}\) ar (ΔABC) ……(iii)
(∵ AQ is the median of ΔABC)
From equation (i) and (ii) we get
ar (ΔAPC) = ar (ΔAQB) ……(A)
From equation (ii) and (iii) we get
ar (ΔAPC) = ar (ΔAQB) …..(iv)
Again, ar (ΔAPQ) = \(\frac {1}{2}\) ar (ΔABQ) ……(v)
(∵ PQ is the median of ΔAQB)
ar (ΔPRQ) = \(\frac {1}{2}\) ar (ΔAPQ)
(∵ QR is the median ΔAQP)
or, ar (ΔPRQ) = \(\frac {1}{2}\) × \(\frac {1}{2}\) ar (ΔABQ) (∵ from equation (v))
= \(\frac {1}{4}\) ar (ΔAQB) (∵ from equation (A))
or, ar (ΔPRQ) = \(\frac {1}{4}\) . 2 ar (ΔARC)
(∵ ar ΔARC = \(\frac {1}{2}\) ar (ΔAPC))
or, ar (ΔPRQ) = \(\frac {1}{2}\) ar (ΔARC)

(ii) In ΔRBC, RQ is the median.
∴ ar (ΔRBQ) = ar (ΔRCQ) …….(I)
(median divide a Δ into tqo equal parts)
But, ar (ΔRBQ) = ar (ΔAQB) – ar (ΔAQR)
= \(\frac {1}{2}\) ar (ΔABC) – \(\frac {1}{8}\) ar (ΔABC)
(∵ ar (ΔAQB) = \(\frac {1}{2}\) ar (ΔABC) and ar(ΔAQR) = \(\frac {1}{8}\) ar (ΔABC))
ar (ΔRBQ) = \(\frac {3}{8}\) ar (ΔABC) ……..(II)
From equation I and II we can say.
ar (ΔRQC) = \(\frac {3}{8}\) ar (ΔABC)

(iii) In ΔABQ, QP is the median
ar (ΔPBQ) = \(\frac {1}{2}\) ar (ΔABQ)
(∵ QP is the median)
= \(\frac {1}{2}\) × \(\frac {1}{2}\) ar (ΔABC)
(∵ ar (ΔABQ) = \(\frac {1}{2}\) ar (ΔABC))
or, ar(ΔPBQ) = \(\frac {1}{4}\) ar(ΔABC) ……(a)
Again, ar (ΔARC) = \(\frac {1}{4}\) ar (ΔACP)
(∵ CR is the median of ΔACP)
= \(\frac {1}{2}\) × \(\frac {1}{2}\) ar (ΔABC)
(∵ ar (ΔACP) = \(\frac {1}{2}\) ar (ΔABC))
or, ar (ΔARC) = \(\frac {1}{4}\) ar (ΔABC) ……(b)
From equation (a) and (b) we get
ar (ΔPBQ) = ar (ΔARC).

Question 8.
In Fig. 9.34, ABC is a right triangle right angled at A. BCFD, ACFG and ABMN are squares on the sides BC, CA, and And AB respectively. Line AX ⊥ DE meets BC at Y. Show that:
(i) ΔMBC ≅ ΔABD
(ii) ar (BYXD) = 2 ar (MBC)
(iii) ar (BYXD) = ar (ABMN)
(iv) ΔFCB ≅ ΔACE
(v) ar (CYXE) = 2 ar (FCB)
(vi) ar (CYXE) = ar (ACFG)
(vii) ar (BCED) = ar (ABMN) + ar (ACFG)

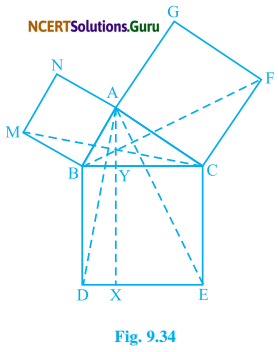
Solution:
(i) In ΔMBC and ΔABD
MB = AB (Sides of square ABMN)
BC = BD (Sides of square BCED)
∠MBA = ∠CBD (each 90°)
or, ∠MBA + ∠ABC = ∠CBD + ∠ABC
or, ∠MBC = ∠ABD
So, By S-A-S congruency condition
ΔMBC ≅ ΔABD …….(i)

(ii) BYXD and ΔABD lie on the same base BD and between the same parallels BD and AX.
∴ ar (BYXD) = 2 ar (ΔABD)
[If a rectangle and a triangle lie on the same base and between same || is then the area of Δ is half of the rectangle]
or, a (DBYXD) = 2 ar (ΔMBC) [from (i) congruent Δ is have equal area]

(iii) We have
ar (BYXD) = 2 ar (ΔMBC) ……(ii)
(Prove above)
and ar (ABMN) = 2 ar (OMBC) …….(iii)
(Because they lie on same base BM and between same || lines MB and NC]
From equation (ii) and (iii)
ar (BYXD) = ar (ABMN)

(iv) In ΔFCB and ΔACE
FC = AC (Sides of square)
CB = CE (Sides of square)
∠FCA = ∠BCE (each 90°)
∠FCA + ∠ACB = ∠BCE + ∠ACB (Add ∠ACB both side)
or, ∠FCB = ∠ACE
So, by S-A-S Congruency Condition
ΔFCB = ΔACE …….(iv)

(v) CYXE and ΔACE lie on samp base CE and between the same parallels CE and AX.
(∵ ar (CYXE) = 2ar (ΔACE))
(If a rectangle and a Δ lie on the same base and between same || lines then ar if the rectangle is double the area of Δ)
or, ar (CYXE) = 2 ar (∠FCB)
(From equ. (iv) congruent Δ have equal area)

(vi) ACFG and ΔFCB lie on same base CF and between same parallels CF and BG.
∴ ar (ACFG) = 2ar (ΔFCB) …….(vi)
From equation (v) and (vi)
ar (CYXE) = ar (ACFG)

(vii) ΔABC, is a right angle triangle right angled at A.
∴ By pythagorus theorem,
BC² = AB² + AC²
or, ar (Square BCED) = ar (Square ABMN) + ar (Square ACFG) [∵ Area of square = (side)²]
ar(BCED) = ar(ABMN) + ar(ACFG).