These NCERT Solutions for Class 9 Maths Chapter 8 Quadrilaterals Ex 8.2 Questions and Answers are prepared by our highly skilled subject experts.
NCERT Solutions for Class 9 Maths Chapter 8 Quadrilaterals Exercise 8.2
Question 1.
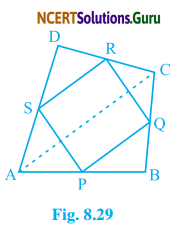
ABCD is a quadrilateral in which P, Q, R, and S are midpoints of the sides AB, BC, CD, and DA (see fig. 8.29). AC is a diagonal. Show that
(i) SR || AC and SR = \(\frac {1}{2}\) AC
(ii) PQ = SR
(iii) PQRS is a parallelogram.
Solution:
Given. ABCD is a quadrilateral in which P, Q, R, and S are the midpoints of side AB, BC, CD, and AD respectively.
To prove that:
(i) SR || AC and SR = \(\frac {1}{2}\) AC
(ii) PQ = SR
(iii) PQRS is a parallelogram.
Proof:
(i) In ΔADC
S and R are the mid-point of side AD and DC respectively.
We know that the line segment joining the midpoints of any two sides of a triangle is parallel to the third side and is half of it.
SR || AC and SR = \(\frac {1}{2}\) AC ……(i)
(ii) In ΔABC,
P and Q are the mid points of side AB and BC respectively.
Therefore, PQ || AC and PQ = \(\frac {1}{2}\) AC …….(ii)
From equation (i) and (ii),
PQ || SR and PQ = SR
(iii) We have
PQ = SR (Prove above)
and PQ || SR (Prove above)
We know that if one pair of opposite sides of a quadrilateral are parallel and equal then the quadrilateral is a parallelogram.
∴ PQRS is parallelogram.
![]()
Question 2.
ABCD is a rhombus and P, Q, R, and S are the midpoints of the sides AB, BC, CD, and DA respectively. Show that the quadrilateral PQRS is a rectangle.
Solution:
Given: Arhmbus ABCD in which P, Q, Rand S are the midpoints of sides AB, BC, CD, and DA respectively. PQ, QR, RS, and SP are joined.
To prove that: PQRS is a rectangle.
Construction: Join AC and BD.
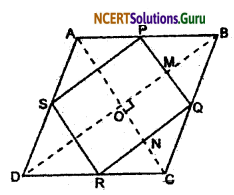
Proof: In order to prove that PQRS is a rectangle, it is sufficient to show that it is a parallelogram whose one angle is a right angle. First, we shall prove that PQRS is a parallelogram.
In ΔABC,
P and Q are the mid points of AB and BC respectively.
∴ PQ || AC and PQ = \(\frac {1}{2}\) AC ……(i)
In ΔADC,
R and S are the mid points of CD and AD respectively.
∴ RS || AC and RS = \(\frac {1}{2}\) AC ……(ii)
From equation (i) and (ii) we have
PQ || RS and PQ = RS
Thus, PQRS is a quadrilateral such that one pair of opposite sides PQ and SR is equal and parallel. So, PQRS is a parallelogram.
PQ || AC (Opposite sides of || gm)
∴ MQ || ON
QR || BD (Opposite sides of || gm)
∴ QN || OM
Therefore, OMQN is a parallelgram.
and ∠NOM = 90°
[Diagomals of a rhombus bisects each other at a right angle]
So, ∠MQN = 90°
[Opposite angles of || gm are equal]
Therefore, PQRS is a parallelogram in which ∠Q is a right angle.
∴ PQRS is a rectangle.
![]()
Question 3.
ABCD is a rectangle and P, Q, R, and S are midpoints of the sides AB, BC, CD, and DA respectively. Show that the quadrilateral PQRS is a rhombus.
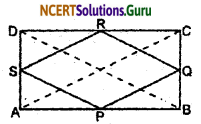
Solution:
Given: A rectangle ABCD in which P, Q, R, and S are the midpoints of sides AB, BC, CD, and DA respectively. PQ, QR, RS, and SP are joined.
To prove that: PQRS is a rhombus.
Construction: Join AC and BD.
Proof: In ∆ABC,
P and Q are mid points of AB and BC respectively.
∴ PQ || AC and PQ = \(\frac {1}{2}\) AC …..(i)
Similarly in ∆ACD,
SR || AC and SR = \(\frac {1}{2}\) AC ……(ii)
From equation (i) and (ii) we have
PQ || SR and PQ = SR
Therefore, PQRS is a parallelogram
∴ SR || PQ (Opposite sides of || gm PQRS)
and SR = PQ
Now, in ∆BCD,
Q and R are mid points of side BC & CD.
∴ QR || AC and QR = \(\frac {1}{2}\) BD
But, AC = BD (In rectangle diagonals are equal)
QR = \(\frac {1}{2}\) AC ……(iii)
From equation (i) and (iii) we have
PQ = QR
but PQ = SR and PS = QR
Therefore, PQ = QR = RS = PS
∴ PQRS is a rhombus.
![]()
Question 4.
ABCD is a trapezium in which AB || DC, BD is a diagonal, and E is the midpoint of AD. A line is drawn through E parallel to AB intersecting BC at F (see fig. 8.30). Show that F is the midpoint of BC.
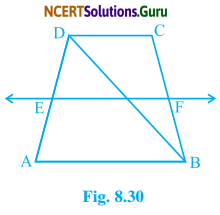
Solution:
In ∆ABD,
E is the midpoints of AD and EF || AB
∴ EF || CD
We know that a line through the midpoint of a side of a triangle parallel to another side bisects the third side. So, G is the midpoint of DB.
Now, in ∆DBC
G is the midpoint of DB and GF || CD
∴ F is the midpoint of BC.
Question 5.
In a parallelogram ABCD, E and F are the midpoints of sides AB and CD respectively (see fig. 8.31). Show that the line segment AF and EC trisect the diagonal BD.
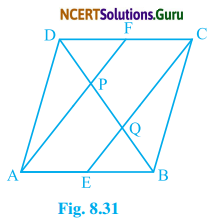
Solution:
We have,
ABCD is a parallelogram
∴ AB || CD
So, AE || FC ……(i)
Again, AB = CD (Opposite sides of ||gm ABCD)
∴ \(\frac {1}{2}\) AB = \(\frac {1}{2}\) CD
or, AE = FC …….(ii)
From equation (i) and (ii)
Therefore, AFCE is a parallelogram.
Now, in ΔDQC,
F is the mid point of CD,
and FP || CQ
We know that a line through the midpoint of a side of a triangle parallel to another side bisects the third side.
So, P is the midpoint of DQ
or, DP = PQ ……(i)
Similarly in ΔAPB, Q is midpoint of BP
i.e. PQ = BQ …..(ii)
From equation (i) and (ii)
PQ = DP = BQ
∴ AF and CE trisect the diagonal BD.
![]()
Question 6.
Show that the line segments joining the midpoints of the opposite sides of a quadrilateral bisect each other.
Solution:
Given: ABCD is a quadrilateral in which P, Q, R, and S are the midpoints of side AB, BC, CD, and AD respectively.
To prove that: PR & QS bisect each other. Construction: Join PQ, QR, RS, and SP and join BD.
Proof: In ΔABD,
S and P are the midpoint of side AD and AB respectively we know that the line segment joining the midpoints of any two sides of a triangle is. parallel to the third side and is half of it.
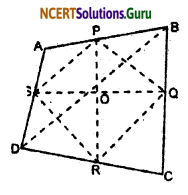
Therefore, SP || BD and SP = \(\frac {1}{2}\) BD …….(i)
Similarly,
In ΔBCD,
Q and R is the mid points of side BC & CD
∴ QR || AC and QR = \(\frac {1}{2}\) AC ……(ii)
From equation (i) and (ii)
SP || QR and SP = QR
We know that if one opposite pair of a quadrilateral are parallel and equal, then the quadrilateral is a parallelogram.
∴ SPQR is a parallelogram.
So, PR and QS bisect each other.
[Because diagonal of a parallelogram bisects each other]
![]()
Question 7.
ABC is a triangle right angled at C. A line through the midpoint M of hypotenuse AB and parallel to BC intersects AC at D. Show that
(i) D is the mid point of AC
(ii) MD ⊥ AC
(iii) CM = MA = \(\frac {1}{2}\) AB
Solution:
Given: ABC is a right-angled triangle right angle at C. M is the midpoint of side AB and DM || BC.
To prove that:
(i) D is the mid point of AC
(ii) MD ⊥ AC
(iii) CM = MA = \(\frac {1}{2}\) AB
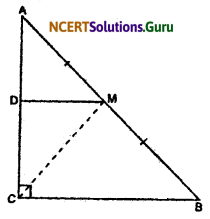
Construction: Join CM.
Proof: (i) In ΔABC,
M is the mid point of side AB and MD || BC
We know that a line through the midpoint of a side of a triangle parallel to another side bisects the third side.
So, D is the midpoint of AC.
(ii) We have DM || CB
∴ ∠MDC + ∠DCB = 180°
(Sum of interior angles of the same side of transveralsi)
or, ∠MDC + 90° = 180°
or, ∠MDC = 90°
Therefore, MD ⊥ AC
![]()
(iii) In ΔAMD and ΔCMD
AD = CD (Prove above)
∠ADM = ∠CDM, (Each 90°)
DM = DM (Common)
By S-A-S congruency condition
ΔAMD ≅ ΔCMD
∴ AM = CM …..(i) (By CPCT)
But AM = AB ……(ii)
(Given M is the mid point of AB)
From (i) and (ii)
CM = MA = \(\frac {1}{2}\) AB