These NCERT Solutions for Class 9 Maths Chapter 7 Triangles Ex 7.3 Questions and Answers are prepared by our highly skilled subject experts.
NCERT Solutions for Class 9 Maths Chapter 7 Triangles Exercise 7.3
Question 1.
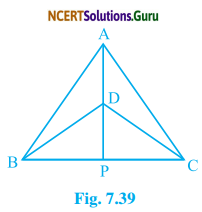
∆ABC and ∆DBC are two isosceles triangles on the same base BC and vertices A and D are on the same side BC (see Fig. 7.39). If AD is extended to intersect BC at P, show that
(i) ∆ABD ≅ ∆ACD
(ii) ∆ABP ≅ ∆ACP
(iii) AP bisects ∠A as well as ∠D.
(iv) AP is the perpendicular bisector of BC
Solution:
(i) In ∆ABD and ∆ACD
AB = AC (∵ ABC is an isosceles ∆)
BD = CD (∵ DBC is an isosceles ∆)
AD = AD (Common)
By S-S-S Congruency condition
∆ABD = ∆ACD
∴ ∠BAD = ∠CAD ……(A) (By C.P.CT)
(ii) In ∆ABP and ∆ACP
AB = AC (∵ ABC is an isoscles ∆)
∠BAP = ∠CAP
AP = AP
By S-A-S Congruency Condition
∠ABP = ∠ACP
Therefore, BP = CP …….(i) (By C.P.C.T.)
![]()
(iii) We have
∆ABD = ∆ACD (From (A))
∴ ∠BAD = ∠CAD (By C.P.C.T.)
∴ AP bisects ∠A
Again,
In ∆BDP and ∆GDP
BD = CD (∵ ∆BDC is an isoscles ∆)
DP = DP (Common)
BP = CP (From equation (i))
By S-S-S Congruency Condition
∆BDP ≅ ∆CDP ………(B)
∴ ∠BDP = ∠CDP (By C.P.C.T)
Therefore, AP bisects ∠D …….(iii)
From equation (ii) and (iii) we can say AP bisects ∠A as well as ∠D.
(iv) we have
∆BDP = ∆CDP (from (B))
∴ BP = CP ……(iv) (By C.P.C.T.)
Again, ∠BPD = ∠CPD (By C.P.C.T.)
Now, ∠BPD + ∠CPD = 180
or, ∠BPD + ∠BPD = 180
2∠BPD = 180
∴ ∠BPD = 90 ……(v)
Therefore, From equations (iv) and (v) we can say AP is the perpendicular bisector of BC.
![]()
Question 2.
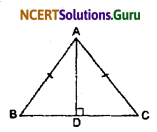
AD is an altitude of an isosceles triangle ABC in which AB = AC. Show that
(i) AD bisects BC
(ii) AD bisects ∠A
Solution:
(i) In ∆ABD and ∆ACD
AB = AC (Given)
∠ADB = ∠ADC (each 90°)
AD = AD (Common)
By R.H.S Congruency Condition
∆ABD = ∆ACD ……(i)
∴ BD = CD (By C.P.C.T.)
Therefore, AD bisects BC.
(ii) We have
∆ABD = ∆ACD (from equation (i))
∴ ∠BAD = ∠CAD (By C.P.C.T.)
Therefore, AD bisects ∠A.
![]()
Question 3.
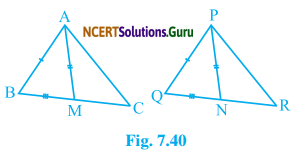
Two sides AB and BC and median AM of one triangle ABC are respectively equal to sides PQ and QR and median PN of ∆PQR (see Fig. 7.40). Show that:
(i) ∆ABM ≅ ∆PQN
(ii) ∆ABC ≅ ∆PQR
Solution:
(i) In ∆ABM and ∆PQN
AB = PQ (Given)
BM = QN (Given)
AM = PN (Given)
By S-S-S Congruency Condition,
∆ABM ≅ ∆PQN …..prove (i)
∴ ∠B = ∠Q (By C.P.C.T)
(ii) Now, In ∆ABC and ∆PQR
AB = PQ (Given)
BM = QN (Given)
∴ 2BM = 2QN
or, BC = QR
(Because M and N are respectively the midpoint of side BC and QR)
∠B = ∠Q (Prove above)
By S-A-S Congruency Condition
∆ABC ≅ ∆PQR …….prove (ii)
![]()
Question 4.
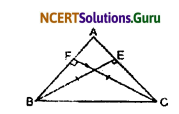
BE and CF are two equal altitudes of a triangle ABC. Using the R.H.S congruence rule, prove that the triangle ABC is isosceles.
Solution:
In ∆BFC and ∆CEB
CR = BE (Given)
∠BFC = ∠CEB (Each 90°)
BC = BC (Common)
∴ By R-H-S congruency condition,
∆BFC ≅ ∆CEB
∴ ∠B = ∠C (By C.P.C.T)
Therefore, AB = AC (Sides opposite to equal angles of a ∆)
Hence, ∆ABC is isosceles.
![]()
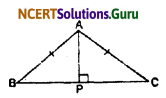
Question 5.
ABC is an isosceles triangle with AB = AC. Draw AP ⊥ BC to show that ∠B = ∠C.
Solution:
In ∆ABP and ∆ACP
AB = AC (Given)
∠APB = ∠APC (Each 90°)
AP = AP (Common)
By R-H-S Congruency Condition,
∆ABP ≅ ∆ACP
or, ∠B = ∠C (By C.P.C.T)