These NCERT Solutions for Class 9 Maths Chapter 13 Surface Areas and Volumes Ex 13.7 Questions and Answers are prepared by our highly skilled subject experts.
NCERT Solutions for Class 9 Maths Chapter 13 Surface Areas and Volumes Exercise 13.7
Question 1.
Find the volume of the right circular cone with
(i) radius 6 cm, height 7 cm.
(ii) radius 3.5 cm, height 12 cm.
Solution:
(i) We have given
radius of right circular cone = 6 cm
and height of right circular cone = 7 cm.
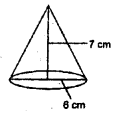
Volume of right circular cone = \(\frac{1}{3} \pi r^{2} h\)
= \(\frac{1}{3} \times \frac{22}{7} 6 \times 6 \times 7\)
= 264 cm3
(ii) We have given
Radius of cone = 3.5 cm
and height of cone = 12 cm.
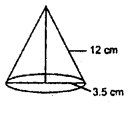
Volume of cone = \(\frac{1}{3} \pi r^{2} h\)
= \(\frac{1}{3} \times \frac{22}{7}\) × 3.5 × 3.5 × 12
= 154 cm3
![]()
Question 2.
Find the capacity in litres of a conical vessel with
(i) radius 7 cm, slant height 25 cm.
(ii) height 12 cm and slant height 13 cm.
Solution:
(i) We have given that,
Radius of conical vessel = 7 cm
and slant height = 25 cm
By Pythagoras theorem,
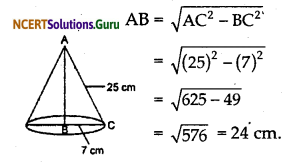
∴ Volume of conical vessel = \(\frac{1}{3} \pi r^{2} h\)
= \(\frac{1}{3} \times \frac{22}{7}\) × 7 × 7 × 24
= 1232 cm3
We know that
1000 cm3 = 1 l
∴ 1232 cm3 = 1.232 l
Therefore, capacity of conical versel is 1.232 litres.
(ii) We have given that
Height of conical vessel (h) = 12 cm
Slant height of conical vessel (l) = 13 cm
By Pythagoras theorem
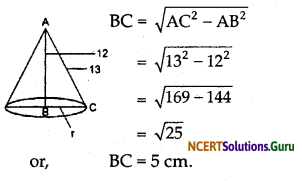
∴ Volume of conical vessel = \(\frac{1}{3} \pi r^{2} h\)
= \(\frac{1}{3} \times \frac{22}{7}\) × 5 × 5 × 12
= \(\frac{2200}{7}\) cm3
Since, 1000 cm3 = 1 l
\(\frac{2200}{7}\) cm3 = \(\frac{2.2}{7}\) l
Therefore, the capacity of conical vessel is \(\frac{2.2}{7}\) litres.
![]()
Question 3.
The height of a cone is 15 cm. If its volume is 1570 cm3, find the radius of the base.
Solution:
We have given
Height of cone (h) = 15 cm
and volume of cone = 1570 cm3
We know that
Volume of cone = \(\frac{1}{3} \pi r^{2} h\)
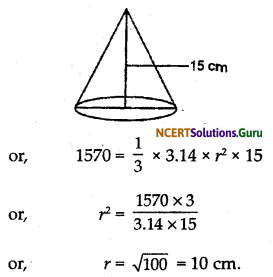
Therfore, radius of required cone = 10 cm.
Question 4.
If the volume of a right circular cone of height 9 cm is 48π cm3, find the diameter of its base.
Solution:
We have given that
Height of cone = 9 cm
and volume of cone = 48π
But we know that volume of cone = \(\frac{1}{3} \pi r^{2} h\)

Therefore diameter of required right circular cone is 2 × 4 = 8 cm.
Question 5.
A conical pit top diameter 3.5 is 12 m deep. What is its capacity in kilo liters.
Solution:
We have given that
diameter of conical pit = 3.5m.
radius of conical pit = \(\frac{3.5}{2}\) m = 1.75 m
and height of conical pit = 12 m
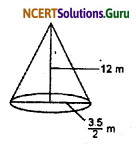
∴ Volume of conical pit = \(\frac{1}{3} \pi r^{2} h\)
= \(\frac{1}{3} \times \frac{22}{7}\) × 1.75 × 1.75 × 12
= 38.5 m3
We know that
1 m3 = 10001
38.5 m3 = 1000 × 38.5
= 38500 litres
= 38.5 kilolitres.
![]()
Question 6.
The volume of a right circular cone is 9856 cm3. If the diameter of the base is 28 cm, find.
(i) height of the cone
(ii) slant height of the cone
(iii) curved surface area of the cone.
Solution:
(i) We have given that
diameter of cone = 28 cm
Radius of cone = 14 cm
and volume of cone = 9856 cm3
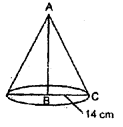
We know that,
Volume of cone = \(\frac{1}{3} \pi r^{2} h\)
9856 = \(\frac{1}{3} \times \frac{22}{7}\) × 14 × 14 × h
h = \(\frac{9856 \times 3 \times 7}{22 \times 14 \times 14}\) = 48 cm
(ii) We have,
height of the cone = 48 cm
and radius of cone = 14 cm
By Pathagoras theorem,
AC = \(\sqrt{\mathrm{AB}^{2}+\mathrm{BC}^{2}}\)
= \(\sqrt{(48)^{2}+(14)^{2}}\)
= \(\sqrt{2304+196}\)
= 50 cm.
Therefore slant height of the cone = 50 cm
![]()
(iii) We know that,
Curved surface area of cone = πrl
= \(\frac {22}{7}\) × 14 × 50
= 2200 cm2
Hence, curved surface area of the cone is 2200 cm2
Question 7.
A right triangle ABC with side 5 cm, 12 cm and 13 cm is revolved about the side 12 cm. Find the volume of the solid so obtained.
Solution:
When we revolved the right ∆ABC about the side 12 cm, then it form a right circular cone of radius 6 cm and height 12 cm.
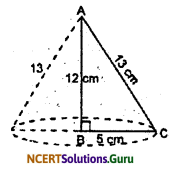
So, volume of such cone = \(\frac{1}{3} \pi r^{2} h\)
= \(\frac {1}{3}\) × π × 5 × 5 × 12
= 100π cm3
Therefore, volume of the solid formed by the revolved a right angle triangle about the side 12 cm is 100π cm3.
Question 8.
If the triangle ABC in the question 7 is revolved about the side 5 cm, then find the volume of the solid so obtained. Find also the ratio of the volumes of the two solid obtained.
Solution:
If we revolved the right angle triangle ABC about the side 5 cm is formed a right circular cone.
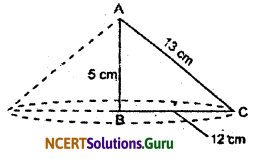
So, volume of the such cone = \(\frac{1}{3} \pi r^{2} h\)
= \(\frac {1}{3}\) × π × 12 × 12 × 5
= 240π
Therefore, volume of the solid formed by the revolved a right angle triangle about the side 5 cm is 240π cm3.
Ratio of the volumes of the two solid obtained by the revolved a right angle triangle is = \(\frac{100 \pi}{240 \pi}\) = 5 : 12
![]()
Question 9.
A heap of wheat is in the form of a cone whose diameter is 10.5 m and height is 3m. Find its volume. The heap is to be covered by canvas to protect it form rain. Find the area of the cavas required.
Solution:
We have given that
Diameter of right circular cone = 10.5 cm
Radius of right circular cone = 3.25 m
and height of the cone = 3m
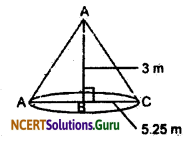
∴ Volume of the cone = \(\frac{1}{3} \pi r^{2} h\)
= \(\frac{1}{3} \times \frac{22}{7}\) × 5.25 × 5.25 × 3
= 86.625 m3
Again,
By Pythagoars theorem.
AC = \(\sqrt{\mathrm{AB}^{2}+\mathrm{BC}^{2}}\)
= \(\sqrt{(3)^{3}+(5.25)^{2}}\)
= \(\sqrt{9+27.5625}\)
= 6.04 m (approx)
Therefore,
Canvas required to covers it = Curved surface area of cone
Now, Curved surface area of cone = πrl
= \(\frac {22}{7}\) × 5.25 × 6.04
= 99.66 m2
Hence, canvas required to cover the conical shape heap of wheat is 99.66 m2.