These NCERT Solutions for Class 9 Maths Chapter 13 Surface Areas and Volumes Ex 13.6 Questions and Answers are prepared by our highly skilled subject experts.
NCERT Solutions for Class 9 Maths Chapter 13 Surface Areas and Volumes Exercise 13.6
Question 1.
The circumference of the base of a cylinderical vessel is 132 cm and its height is 25 cm. How many liters of water can it hold? (1000 cm3 = 1L)
Solution:
We have given that
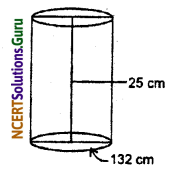
Circumference of base of cylinder = 132 cm
2πr = 132
⇒ r = \(\frac{132 \times 7}{22 \times 2}\) = 21 cm
and height of cylinderical vessel = 25 cm
Volume of cylindrical vessel = πr2h
= \(\frac {22}{7}\) × 21 × 21 × 25
= 34650 cm3
Now, we know that 1000 cm3 = 1L
34650 cm3 = 34.65 L
Therefore, the cylindrical vessel can hold 34.65 liters of water.
![]()
Question 2.
The inner diameter of a cylindrical wooden pipe is 24 cm and its outer diameter is 28 cm. The length of the pipe is 35 cm. Find the mass of the pipe, if 1 cm3 is wood has a mass of 0.6 g.
Solution:
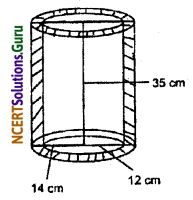
Volume of required wood = volume of outer cylinder – volume of inner cylinder.
= π(14)2 × 35 – π(12)2 × 35
= \(\frac {22}{7}\) × 35((14)2 – (12)2)
= \(\frac {22}{7}\) × 35 × (196 – 144)
= \(\frac {22}{7}\) × 35 × 52
= 5720 cm3
Now, we have given that, mass of 1 cm3 of wood = 0.6
Therefore, mass of 5720 cm3 of wood = 0.6 × 5720 g.
= 3432g
= 3.432 kg.
Question 3.
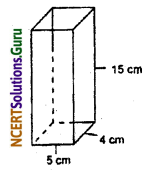
A soft drink is available in two packs — (i) a tin can with a rectangular base of length 5 cm and wide 4 cm having a height of 15 cm and (ii) a plastic cylinder with a circular base of diameter 7 cm and height 10 cm. Which container has greater capacity and by how much.
Solution:
In the first case,
The tin can with a rectangular base of length 5 cm and wide 4 cm having a height of 15 cm.
∴ The volume of this can = l × b × h
= 15 × 4 × 5
= 300 cm3 …….(i)
In the second case,
The circular plastic cylinder has a base diameter is 7 cm and the height of the cylinder is 10 cm.
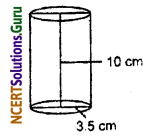
∴ Volume of plastic cylinder = πr2h
= \(\frac {22}{7}\) × 3.5 × 3.5 × 10
= 385 cm3 ……(ii)
From (i) and (ii), it is clear that
The volume of the circular cylinder has a greater capacity of 85 cm3.
![]()
Question 4.
If the lateral surface of a cylinder is 94.2 cm3 and its height is 5 cm, then find
(i) radius of its base
(ii) volume of the cylinder.
Solution:
(i) We have given that lateral surface of cylinder = 94.2 cm3 and height is 5 cm.
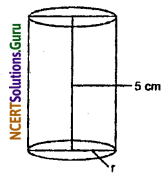
Now, we know that, lateral surface area of cylinder = 2πrh
94.2 = 2 × 3.14 × r × 5
r = \(\frac{94.2}{2 \times 3.14 \times 5}\) = 3 cm
(ii) We know that
Volume of cylinder = 2πrh
= 3.14 × 3 × 3 × 5
= 141.3 cm3.
Question 5.
It costs Rs. 2200 to paint the inner curved surface of a cylindrical vessel 10 m deep. If the cost of painting is at the rate of Rs. 20 per m2, Find.
(i) Inner curved surface area of the vessel.
(ii) radius of the base.
(iii) capacity of the vessel.
Solution:
(i) We have given that
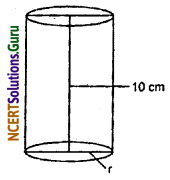
Rate of painting = Rs. 20 per m2
and total cost of curved surface area of cylindrical vessel = Rs. 2200
It means that inner curved surface area of cylindrical vessel = \(\frac{2200}{20}\) = 110 m2
(ii) we know that curved surface ara of cylinder = 2πrh
⇒ 110 = 2 × \(\frac {22}{7}\) × r × 10
⇒ r = \(\frac{110 \times 7}{2 \times 22 \times 10}\) = 1.75 m
(iii) We know that volume of cylinder = πr2h
= \(\frac {22}{7}\) × 1.75 × 1.75 × 10
= 96.25 m3
Therefore, Capacity of the vessel = 96.25 m3 = 96.25 kl
(1 m3 = 1000 l =1 kl)
![]()
Question 6.
The capacity of a closed cylindrical vessel of height 1 m is 15.4 liters. How many square meters of the metal sheet would be needed to make it?
Solution:
We have given that
Capacity of closed cylindrical vessel = 15.41 = \(\frac{15.4}{1000}\) m3
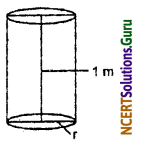
and height of the cylindrical vessel = 1 m.
We know that,
volume of cylinder = πr2h
⇒ \(\frac{15.4}{1000}\) = \(\frac {22}{7}\) × r2 × 1
⇒ r2 = 0.0049
⇒ r = 0.07m
Now, Total surface area of cylindrical vessel = 2πr(h + r)
= 2 × \(\frac {22}{7}\) × 0.07 (1 + 0.07)
= 0.4708 m2
Therefore, a metal sheet would be needed to make the required cylinder is 0.4708 m2.
Question 7.
A lead pencil consists of a cylinder of wood will a solid cylinder of graphite filled in the interior. The diameter of the pencil is 7 mm and the diameter of the graphite is 1 mm. If the length of the pencil is 14 cm, find the volume of the wood and that of the graphite.
Solution:
We have given that
Diameter of pencil = 7 mm
Radius of pencil = 3.5 mm
and height of pencil = 14 cm = 140 mm
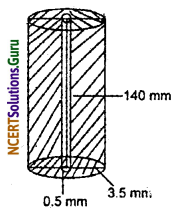
Volume of pencil = πr2h
= \(\frac {22}{7}\) × 3.5 × 3.5 × 140
= 5390 mm3
Agian, we have
Diamter of lead = 1 mm
Radius of lead = 0.5 mm
and height of lead = 14 cm = 140 mm
Volume of lead = πr2h
= \(\frac {22}{7}\) × 0.5 × 0.5 × 140
= 110 mm3
Volume of graphite = 110 mm3 = 0.11 cm3
and volume of wood = 5390 – 110
= 5280 mm3
= 5.28 cm3
![]()
Question 8.
A patient in a hospital is given soup daily in a cylindrical bowl of diameter 7 cm. If the bowl is filled with soup to a height of 4 cm, how much soup the hospital has to prepare daily to serve 250 patients?
Solution:
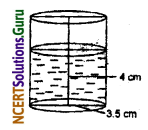
We have given that
Diameter of pencil = 7 mm
Radius of cylindrical bowl = 3.5 cm
and height of soup to serve = 4 cm.
Volume of soup to serve one patient = πr2h
= \(\frac {22}{7}\) × 3.5 × 3.5 × 4
= 154 cm3
Therefore, volume of soup to serve 250 patients are = 250 × 154
= 38500 cm3.
= 38.5 litre.
Hence, Hospital has to prepare daily 38.5 litres of soup to serve 250 patients.