NCERT Solutions for Class 9 Maths Chapter 10 Circles Ex 10.6

These NCERT Solutions for Class 9 Maths Chapter 10 Circles Ex 10.6 Questions and Answers are prepared by our highly skilled subject experts.

NCERT Solutions for Class 9 Maths Chapter 10 Circles Exercise 10.6

Question 1.
Prove that the line of centres of two intersecting circles subtends equal angles at the two points of intersection.
Solution:
Given: Two circles of centre O and O’ intersect each other at A and B.
To prove that: ∠OAO’ = ∠OBO’
Construction: Join OO’.
Proof: In ∆AOO’ and ∆BOO’
AO = BO (Radii of the same circle)
AO’ = BO’ (Radii of the same circle)
OO’ = OO’ (Common)
So, by S-S-S congruency condition
∆AOO’ ≅ ∆BOO’
∴ ∠OAO’ = ∠OBO’ (By CPCT)

Question 2.
Two chords AB and CD of lengths 5 cm and 11 cm respectively of a circle are parallel to each other and are on opposite sides of its centre. If the distance between AB and CD is 6 cm, find the radius of the circle.
Solution:
Let O be the centre of the given circle and let its radius be r cm.
Draw OM ⊥ AB and ON ⊥ CD.
Since OM ⊥ AB, ON ⊥ CD, and AB || CD.
Therefore point M, O and N are collinear. So MN = 6 cm.
Let OM = x cm, Then ON = 6 – x cm
Join OA and OC, then OA = OC = r.
Since the perpendicular from the centre to a chord of the circle bisect the chord.

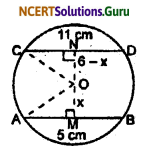
∴ AM = MB = \(\frac {5}{2}\) cm
and CN = ND = \(\frac {11}{2}\) cm.
In right triangle OAM,
OA² = OM² + AM²
r² = x² + \(\left(\frac{5}{2}\right)^{2}\) ……(i)
Now, in right triangle OCN
OC² = ON² + CN²
r² = (6 – x)² + \(\left(\frac{11}{2}\right)^{2}\) …….(ii)
From equation (i) and (ii)
\(x^{2}+\left(\frac{5}{2}\right)^{2}=(6-x)^{2}+\left(\frac{11}{2}\right)^{2}\)

Hence, the radius of the circle is \(\frac{5 \sqrt{5}}{2}\) cm.

Question 3.
The length of two parallel chords of a circle are 6 cm and 8 cm. If the smaller chord is at distance of 4 cm from the centre, what is the distance of the other chord from the centre.
Solution:
Let AB and CD be two parallel chords of a circle with centre O such that AB = 6 cm and CD = 8 cm.
Let the radius of the circle be r cm.
Draw OP ⊥ AB and OQ ⊥ CD.
The length of OP is 4 cm.

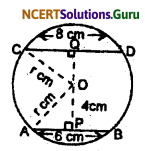
In right triangle OAP,
r² = OP² + AP²
⇒ r² = (4)² + (3)² [∵ AP = \(\frac {1}{2}\) AB = 3 cm]
⇒ r² = 16 + 9 = 25
⇒ r = 5 cm ……(i)
Now, in right triangle OQC,
r² = (OQ)² + (CQ)²
⇒ (5)² = (OQ)² + (4)²
[∵ r = 5 cm prove above and CQ = \(\frac {1}{2}\) CD = 4 cm]
⇒ 25 = (OQ)² + 16
⇒ (OQ)² = 25 – 16 = 9
⇒ OQ = 3 cm
Therefore the distance of the chord CD from the centre is 3 cm.

Question 4.
Let the vertex of an angle ABC be located outside a circle and let the sides of the angle intersect equal chords AD and CE with a circle. Prove that ∠ABC is equal to half the difference of the angles subtended by the chords AC and DE at the centre.
Solution:
Given: Vertex of an angle ABC be located outside a circle, and AD = CE.
Let ∠AOC = ∠x, ∠AOD = ∠z and ∠DOE = ∠y.

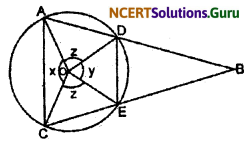
To prove that: ∠ABC = \(\frac {1}{2}\) (x – y)
Proof: AD = CE (given)
∴ ∠AOD = ∠COE (Angle made by equal chord at the centre are equal)
Therefore,
∠x + ∠y + ∠z + ∠z = 360°
⇒ ∠x + ∠y + 2∠z = 360°
⇒ 2∠z = 360° – ∠x – ∠y
⇒ ∠z = 180 – \(\frac {1}{2}\) ∠x – \(\frac {1}{2}\) ∠y ……(A)
Now, ∠ODB = ∠OAD + ∠DOA
(Exterior angle is equal to sum of opposite interior angles)
∠ODB = ∠OAD + ∠z ……(i)
Again, ∠OAD + ∠z + ∠ODA = 180°
(Sum of all three angles of triangles)
or, ∠OAD + ∠z + ∠OAD = 180°
(Angle opposite to equal sides are equal and OA = OD radii of circle)
or, 2∠OAD = 180° – ∠z
or, ∠AOD = \(\frac {1}{2}\) (180° – ∠z) = 90° – \(\frac {1}{2}\) ∠z
Putting the value of ∠AOD in equation (i)
∴ ∠ODB = 90° – \(\frac {1}{2}\) ∠z + ∠z
(∵ ∠OAD = 90° – \(\frac {1}{2}\) ∠z)
or, ∠ODB = 90° + \(\frac {1}{2}\) ∠z ……..(ii)
Similarly, ∠OEB = 90° + \(\frac {1}{2}\) ∠z ……(iii)
Now, in ODBE
∠ODB + ∠B + ∠OEB + ∠y = 360°
(Sum of all angle of ∆ is 360°)
90 + \(\frac {1}{2}\) ∠z + ∠B + 90 + \(\frac {1}{2}\) ∠z + ∠y = 360°
(Use equation (ii) and (iii))
or, 180 + ∠z + ∠B + ∠y = 360
or, ∠B = 180 – ∠y – ∠z …..(iv)
⇒ ∠ABC = \(\frac {1}{2}\) [(Angle subtended by the chorde DE at the centre) – (Angle subtended by the chord AC at the centre)]
⇒ ∠ABC = \(\frac {1}{2}\) [(Difference of the angles subtended by the chorde DE and AC at the centre)]

Question 5.
Prove that the circle drawn with any side of a rhombus as diameter passes through the point of intersection of its diagonals.
Solution:
We have a rhombus ABCD such that its diagonals AC and BD intersect at O.
P, Q, R and S are the mid-points of DC, AB, AD and BC respectively
∴ \(\frac {1}{2}\) AD = \(\frac {1}{2}\) BC
⇒ RA = SB
⇒ RA = OQ ……(ii)
[∴ PQ is drawn parallel to AD and AD = BC]
⇒ \(\frac {1}{2}\) AB = \(\frac {1}{2}\) AD
⇒ AQ = AR ……(iii)
From (i), (ii) and (iii), we have
AQ = QB = OQ
i.e., A circle drawn with Q as centre, will pass through A, B and O.
Thus, the circle passes through the intersection ‘O’ of the diagonals rhombus ABCD.

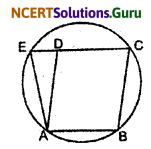
Question 6.
ABCD is a parallelogram. The circle through A, B, and C intersect CD (produced if necessary) at E. Prove that AE = AD.
Solution:
We have a circle passing through A, B, and C is drawn such that it intersects CD at E.
∴ ∠AEC + ∠B = 180° ……(i)
[Opposite angles of a cyclic quadrilateral are supplementary]
But ABCD is a prallelogram (Given)
∴ ∠D = ∠B ……(ii)
[Opposite angles of a parallelogram are equal]
From (i) and (ii), we have
∠AEC + ∠D = 180° …….(iii)
But ∠AEC + ∠AED = 180° (Linear pair) ……(iv)

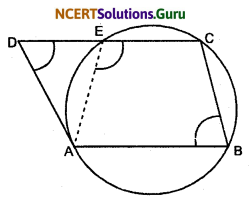
From (iii) and (iv),
We have ∠D = ∠AED
i.e., The base angles of ∆ADE are euqal.
∴ AE = AD

Question 7.
AC and BD are chords of a circle which bisects each other. Prove that
(i) AC and BD are diameters
(ii) ABCD is a rectangle.
Solution:
Given: A circle in which two chords AC and BD are such that they bisect each other.
Let their point of intersection be O.
To Prove: (i) AC and BD are diameters.
(ii) ABCD is a rectangle.
Construction: Join AB, BC, CD, and DA.
Proof: (i) In ∆AOB and ∆COD, we have

(∵ ∠ADC = ∠ABC, opposite angles of || gm ABCD)
From equation (i) and (ii)
∠AED + ∠ABC = ∠ADE + ∠ABC
or, ∠AED = ∠ADE
Thus, in ∆AED, we have
∠AED = ∠ADE
∴ AD = AE. (Side opposite to equal angles are equal)

Question 8.
Bisectors of angles A, B and C of a triangle ABC intersect its circumcircle at D, E and F respectively. Prove that the angle of the triangle DEF are 90° – \(\frac {1}{2}\) ∠A, 90° – \(\frac {1}{2}\) ∠B and 90° – \(\frac {1}{2}\) ∠C.
Solution:
Given: In ∆ABC, AD, BE and CF is the angle bisector of ∠A, ∠B, and ∠C respectively.
Where D, E, and F lie on the circumcircle of ∆ABC.

To prove that:
(i) ∠FDE = 90° – \(\frac {1}{2}\) ∠A
(ii) ∠DEF = 90° – \(\frac {1}{2}\) ∠B
(iii) ∠EFD = 90° – \(\frac {1}{2}\) ∠C
Proof:
(i) ∠ADF = ∠ACF ……(i) (Angles in the same segments of a circle are equal)
Again, ∠ADE = ∠ABE ……(ii) (Angles in the same segment of atcircle are equal)
Adding (i) and (ii)
∠APF + ∠ACF = ∠ACF + ∠ABE
or, ∠FDE = \(\frac {1}{2}\) ∠C + \(\frac {1}{2}\) ∠B ……(iii)
(∵ CF and BE are the bisector of ∠B and ∠C respectively)
Now, In ∆ABC
∠A + ∠B + ∠C = 180° (Sum of all angles of a ∆ is 180°)
or, \(\frac {1}{2}\) (∠A + ∠B + ∠C) = 90°
or, \(\frac {1}{2}\) ∠B + \(\frac {1}{2}\) ∠C = 90 – \(\frac {1}{2}\) ∠A ……(iv)
From equation (iii) and (iv)
∠FDE = 90° – \(\frac {1}{2}\) ∠A
Similarly we can prove
(ii) ∠DEF = 90 – \(\frac {1}{2}\) ∠B
(iii) ∠EFD = 90 – \(\frac {1}{2}\) ∠C.

Question 9.
Two congruent circles intersect each other at points A and B. Through A any line segment PAQ is drawn so that P, Q, lie on the two circles. Prove that BP = BQ.
Solution:
Let C(0, r) and C(O’, r) be two congruent circles.

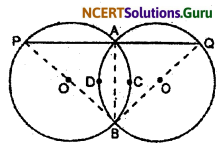
Since AB is a common chord of two congruent circles. Therefore,
arc ACB = arc ADB
∴ ∠BPA = ∠BQA
Thus, in ∆BPQ, we have ∠BPA = ∠BQA
∴ BP = BC (Sides opposite to equal angles of a triangle are equal)

Question 10.
In any triangle ABC, if the angle bisector of ∠A and perpendicular bisector of BC intersect, prove that they intersect on the circumcircle of the triangle ABC.
Solution:
Given: ABC is a triangle in which the bisector of ∠A intersects the circumcircle of ∆ABC at D.
To prove that: Perpendicular bisector of side BC intersects the angle bisector of ∠A at D.

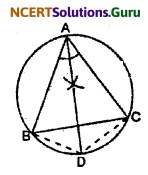
Construction: Join BD and CD.
Proof: ∠BCD = ∠BAD ……(i)
(Angles in the same segment of a circle are equal)
Again, ∠DBC = ∠DAC …….(ii)
(Angles in the same segment of a circle are equal)
But, ∠BAD = ∠DAC …..(iii)
(∵ AD is the bisector of ∠A)
From equation (i), (ii) and (iii)
∠BCD = ∠DBC
or, BD = CD (Side opposite to equal angles of a ∆ are equal)
So, D must be lying on the perpendicular bisector of BC.
Therefore, the perpendicular bisector of side BC intersects the angle bisector of ∠A).