NCERT Solutions for Class 9 Maths Chapter 10 Circles Ex 10.4

These NCERT Solutions for Class 9 Maths Chapter 10 Circles Ex 10.4 Questions and Answers are prepared by our highly skilled subject experts.

NCERT Solutions for Class 9 Maths Chapter 10 Circles Exercise 10.4

Question 1.
Two circles of radii 5 cm and 3 cm intersect at two points and the distance between their centres is 4 cm. Find the length of the common chord.
Solution:
Two circles with centre O, and A having radius 5 cm and 3 cm respectively.
The distance between the centres i.e. OA = 4 cm CD is the common chord. OA is perpendicular to CD and bisects CD.

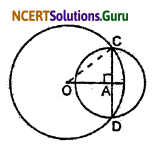
OA ⊥ CD and AC = AD
In ∆OAC, OC = 5 cm, OA = 4 cm.
By Pythagoras theorem
AC² = OC² – OA²
⇒ AC² = 9
⇒ AC = 3 cm
Hence CD passes through the centre of a smaller circle and equal to the diameter of the circle.
CD = 2AC = 2 × 3 = 6 cm

Question 2.
If two equal chords of a circle intersect within the circle, prove that the segments of one chord are corresponding segments of the other chord.
Solution:
Given: AB and CD are two equal chords of the circle which intersect each other at P.

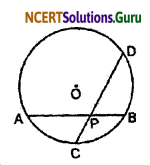
To prove that: Segment ACB ≅ Segment CBD.
Proof: We have given,
chord AB = chord CD
∴ \(\widetilde{\mathrm{AB}} \cong \widetilde{\mathrm{CD}}\)
We know that, the segment made between congruent arcs and equal chords are congruent.
∴ Segment ACB ≅ Segment CBD.

Question 3.
If two equal chords of a circle intersect within the circle, prove that the line joining the point of intersection to the centre makes equal angles with the chords.
Solution:
Given: AB and CD are two equal chords of a circle whose centre is O. Chord AB and CD intersect each other at E.

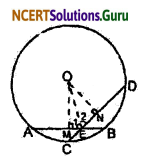
To prove that: ∠1 = ∠2
Construction: Draw OM ⊥ AB and ON ⊥ CD, and join OE.
Proof: In ∆OME and ∆ONE
OM = ON (Equal chords are equidistance from the centre)
∠OME = ∠ONE (Each 90°)
OE = OE (Common)
So, by R-H-S congruency condition
∆OME ≅ ∆ONE
∠1 = ∠2 (By CPCT)

Question 4.
If a line intersects two concentric circles (circles with the same centre) with centre O at A, B, C and D. Prove that AB = CD (see Fig. 10.25)

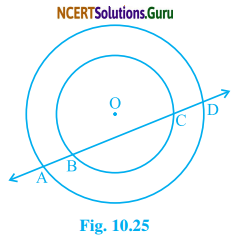
Solution:
Let OM be perpendicular from O on line l.
We know that the perpendicular from the centre of a circle to a chord; bisect the chord. Since BC is a chord of the smaller circle and OM ⊥ BC.
∴ BM = CM ……(i)
Again, AD is a chord of the larger circle and OM ⊥ AD.
∴ AM = DM ……(ii)
Subtracting equation (i) from (ii), we get
AM – BM = DM – CM
or, AB = CD.

Question 5.
Three girls Reshma, Salma, and Mandeep are playing a game by standing on & circle of radius 5 m drawn in a park. Reshma throws a ball to Salma, Salma to Mandip, Mandip to Resma. If the distance between Reshma and Salma and between Salma and Mandip is 6 m each, what is the distance between Reshma and Mandip?
Solution:
Let Reshma, Salma and Mandip are standing on the point R, S, and M respectively where O is the centre of the circle.

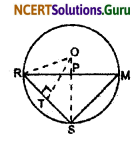
RS = SM = 6m
OR = 5m
∆RSM is Issosclus Triangle
∴ SP ⊥ RM and also P is mid-point of RM
RP = PM
ar (∆ORS) = \(\frac {1}{2}\) × OS × PR
= \(\frac {1}{2}\) × 5 × x …….(i)
Draw OT ⊥ RS here OR = OS (Radii of circle)
So, ∆ORS is Issosceles Triangle
∴ RT = TS = 3 cm
In right ∆OTS,
OS = 5 cm, TS = 3 cm
Using Pythagoras theorem,
OT² = OS² – TS²
⇒ OT² = (5)² – (3)²
⇒ OT² = 16
⇒ OT = √16 = 4 cm
Again, ar (∆ORS) = \(\frac {1}{2}\) × RS × OT
= \(\frac {1}{2}\) × 6 × 4 ……(ii)
From equation (i) and (ii)
\(\frac {1}{2}\) × 5 × x = \(\frac {1}{2}\) × 6 × 4
or \(\frac {5x}{2}\) = 12
x = \(\frac{12 \times 2}{5}=\frac{24}{5}\)
We have to calculate
RM = 2RP = 2 × \(\frac{24}{5}\) = \(\frac{48}{5}\)
∴ RM = 9.6 m
Distance between Reshma and Mandip is equal to 9.6 m.

Question 6.
A circular park of a radius of 20 m is situated in a colony. Three boys Ankur, Syed, and David are sitting at an equal distance on its boundary each having a toy telephone in his hands to talk to each other. Find the length of the string of each phone.
Solution:
Let three boys Ankur, Syed and David are sitting on the point A, B, and C respectively.
O is the centre of the circle.
According to question AB = BC = CA = x (Let)

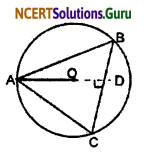
So, ∆ABC is an equilateral triangle
OA = OB = OC = Radius of die circle = 20 meter
Join A, O and extand to D.
As ∆ABC is an equilateral triangle
\(\frac{\mathrm{OA}}{\mathrm{OD}}=\frac{2}{1}\)
or \(\frac{\mathrm{20}}{\mathrm{OD}}=\frac{2}{1}\) (∵ OA = 20 m)
OD = 10 meter
In right angle triangle ACD
(AD)² = (CD)² + (AD)²
⇒ (x)2 = \(\left(\frac{x}{2}\right)^{2}\) + (30)² (∵ AD ⊥ BC and D is the mid point)
⇒ x² = \(\frac{x^{2}}{4}\) + 900
⇒ x² – \(\frac{x^{2}}{4}\) = 900
⇒ \(\frac{4 x^{2}-x^{2}}{4}\) = 900
⇒ \(\frac{3 x^{2}}{4}\) = 900
⇒ x² = \(\frac{900 \times 4}{3}\)
⇒ x² = 1200
⇒ x = √1200
⇒ x = 20√3 meteres
Therefore, the length of the string of each phone is 20√3 meters.