These NCERT Solutions for Class 8 Maths Chapter 6 Square and Square Roots Ex 6.3 Questions and Answers are prepared by our highly skilled subject experts.
NCERT Solutions for Class 8 Maths Chapter 6 Square and Square Roots Exercise 6.3
Question 1.
What could be the possible ‘ones’ digits of the square root of each of the following numbers?
(i) 9801
(ii) 99856
(iii) 998001
(iv) 657666025
Solution:
(i) The unit’s digit of the square root of the number 9801 could be 1 or 9 [1 × 1 = 1, 9 × 9 = 81]
(ii) The units digit of the square root of the number 99856 could be 4 or 6 [4 × 4 = 16 or 6 × 6 = 36]
(iii) The unit’s digit of the square root of the number 998001 could be 1 or 9 [1 × 1 = 1 or 9 × 9 = 81]
(iv) The units digit of the square root of the number 657666025 could be 5 [5 × 5 = 25]
![]()
Question 2.
Without doing any calculation, find the numbers which are surely not perfect squares.
(i) 153
(ii) 257
(iii) 408
(iv) 441
Solution:
We know that the ending digit of a perfect square is 0, 1, 4, 5, 6 and 9
A number ending in 2, 3, 7, or 8 can never be a perfect square
(i) 153 cannot be a perfect square.
(ii) 257 cannot be a perfect square.
(iii) 408 cannot be a perfect square.
(iv) 441 can be a perfect square.
Question 3.
Find the square roots of 100 and 169 by the method of repeated subtraction.
Solution:
(i) √100
100 – 1 = 99
99 – 3 = 96
96 – 5 = 91
91 – 7 = 84
84 – 9 = 75
75 – 11 = 64
64 – 13 = 51
51 – 15 = 36
36 – 17 = 19
19 – 19 = 0
∴ We reach at 0 by successive subtraction of 10 odd numbers
∴ √100 = 10
![]()
(ii) √169
169 – 1 = 168
168 – 3 = 165
165 – 5 = 160
160 – 7 = 153
153 – 9 = 144
144 – 11 = 133
133 – 13 = 120
120 – 15 = 105
105 – 17 = 88
88 – 19 = 69
69 – 21 = 48
48 – 23 = 25
25 – 25 = 0
∴ We reach at 0 by successive subtraction of 13 odd numbers
∴ √169 = 13
Question 4.
Find the square roots of the following numbers by the Prime Factorisation Method.
(i) 729
(ii) 400
(iii) 1764
(iv) 4096
(v) 7744
(vi) 9604
(vii) 5929
(viii) 9216
(ix) 529
(x) 8100
Solution:
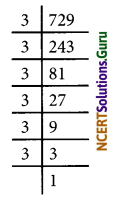
(i) √729
= \(\sqrt{3^{2} \times 3^{2} \times 3^{2}}\)
= 3 × 3 × 3
= 27
∴ √729 = 27
(ii) √400
= \(\sqrt{2^{4} \times 5^{2}}\)
= 22 × 5
= 20
∴ √400 = 20

![]()
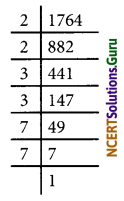
(iii) √1764
= \(\sqrt{2^{2} \times 3^{2} \times 7^{2}}\)
= 2 × 3 × 7
= 42
∴ √1764 = 42
(iv) √4096
= \(\sqrt{2^{12}}\)
= 26
= 2 × 2 × 2 × 2 × 2 × 2
= 64
∴ √4096 = 64

(v) √7744
= \(\sqrt{2^{6} \times 11^{2}}\)
= 23 × 11
= 88
∴ √7744 = 88

(vi) √9604
= \(\sqrt{2^{2} \times 7^{4}}\)
= 2 × 72
= 2 × 49
= 98
∴ √9604 = 98

(vii) √5929
= \(\sqrt{7^{2} \times 11^{2}}\)
= 7 × 11
= 77
∴ √5929 = 77

(viii) √9216
= \(\sqrt{2^{5} \times 3^{2}}\)
= 25 × 3
= 2 × 2 × 2 × 2 × 2 × 3
= 32 × 3
= 96
∴ √9216 = 96

![]()
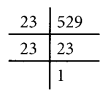
(ix) √529
= \(\sqrt{23^{2}}\)
= 23
∴ √529 = 23
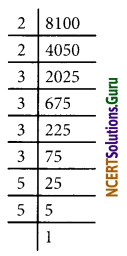
(x) √8100
= \(\sqrt{2^{2} \times 3^{4} \times 5^{2}}\)
= 2 × 32 × 5
= 2 × 9 × 5
= 90
∴ √8100 = 90
Question 5.
For each of the following numbers, find the smallest whole number by which it should be multiple so as to get a perfect square number. Also, find the square root of the square number so obtained.
(i) 252
(ii) 180
(iii) 1008
(iv) 2028
(v) 1458
(vi) 768
Solution:
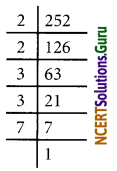
(i) 252 = 22 × 32 × 7
The prime factor 7 has no pair
∴ The number 252 should be multiply by 7 to get a perfect square number 252 × 7 = 1764
√1764
= \(\sqrt{2^{2} \times 3^{2} \times 7^{2}}\)
= 2 × 3 × 7
= 42
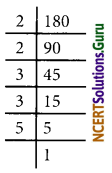
(ii) 180 = 22 × 32 × 5
The prime factor 5 has no pair
∴ The number 180 should be multiplied by 5 to get a perfect square number 180 × 5 = 900
√900
= \(\sqrt{2^{2} \times 3^{2} \times 5^{2}}\)
= 2 × 3 × 5
= 30
![]()
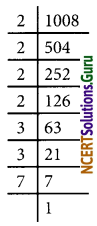
(iii) 1008 = 24 × 32 × 7
The prime factor 7 has no pair
∴ The number 1008 should be multiplied by 7 to get a perfect square number 1008 × 7 = 7056
√7056
= \(\sqrt{2^{4} \times 3^{2} \times 7^{2}}\)
= 4 × 3 × 7
= 84
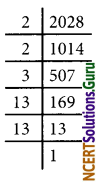
(iv) 2028 = 22 × 33 × 132
The Prime factor 3 has no pair
∴ The number 2028 should be multiplied by 3 to get a perfect square number 2028 × 3 = 6084
√6084
= \(\sqrt{2^{2} \times 3^{2} \times 13^{2}}\)
= 2 × 3 × 13
= 78
(v) 1458 = 2 × 36
The prime factor 2 has no pair
∴ The number 1458 should be multiplied by 2 to get perfect square number 1458 × 2 = 2916
√2916
= \(\sqrt{2^{2} \times 3^{6}}\)
= 2 × 33
= 2 × 3 × 3 × 3
= 54
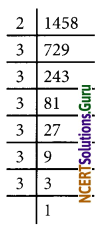
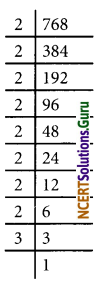
(vi) 768 = 28 × 3
∴ The prime factor 3 has no pair
∴ The number 768 should be multiply be 3 to make it a perfect square.
768 × 3 = 2304
√2304
= \(\sqrt{2^{8} \times 3^{2}}\)
= 24 × 3
= 2 × 2 × 2 × 2 × 3
= 48
Question 6.
For each of the following numbers, find the smallest whole number by which it should be divided so as to get a perfect square. Also, find the square root of the square number so obtained
(i) 252
(ii) 2925
(iii) 396
(iv) 2645
(v) 2800
(vi) 1620
Solution:
(i) 252 = 22 × 32 × 7
The prime factor 7 has no pair
∴ The given number should be divided by 7 to get a perfect square
\(\frac{252}{7}=\frac{2^{2} \times 3^{2} \times 7}{7}\) = 36
√36
= \(\sqrt{2^{2} \times 3^{2}}\)
= 2 × 3
= 6
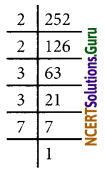
![]()
(ii) 2925 = 32 × 52 × 13
The prime factor 13 has no pair
∴ The given number should be divided by 13 to get a perfect square
\(\frac{2925}{13}=\frac{3^{2} \times 5^{2} \times 13}{13}\)
= 9 × 25
= 225
√225
= \(\sqrt{3^{2} \times 5^{2}}\)
= 3 × 5
= 15

(iii) 396 = 22 × 32 × 11
The prime factor 11 has no pair.
∴ The given no. should be divided by 11 to get a perfect square
\(\frac{396}{11}=\frac{2^{2} \times 3^{2} \times 11}{11}\)
= 4 × 9
= 36
√36
= \(\sqrt{2^{2} \times 3^{2}}\)
= 2 × 3
= 6

(iv) 2645 = 5 × 232
The prime factor 5 has no pair.
∴ The given number should be divided by 5 to get a perfect square
\(\frac{2645}{5}=\frac{5 \times 23^{2}}{5}\) = 232 = 529
√529 = \(\sqrt{23^{2}}\) = 23
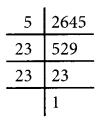
(v) 2800 = 24 × 52 × 7
The prime factor 7 has no pair
∴ The given number should be divided by 7 to get a perfect square
\(\frac{2800}{7}=\frac{2^{4} \times 5^{2} \times 7}{7}\)
= 24 × 52
= 16 × 25
= 400
√400 = 20
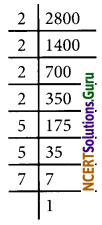
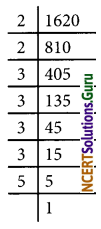
(vi) 1620 = 22 × 34 × 5
The prime factor 5 has no pair.
The given number should be divided by 5 to get a perfect square
\(\frac{1620}{5}=\frac{2^{2} \times 3^{4} \times 5}{5}\)
= 22 × 34
= 4 × 81
= 324
√324
= \(\sqrt{2^{2} \times 3^{4}}\)
= 2 × 32
= 2 × 9
= 18
![]()
Question 7.
The students of class VIII of a school donated ₹ 2401 in all, for Prime Minister National Relief Fund. Each student donated as many rupees as the number of students in the class. Find the number of students in the class.
Solution:
Let the number of students be ‘x’
Amount donated by each student = x
Total amount donated by the class = ₹ x × x = ₹ x2
Given, x2 = 2401
x = √2401
= \(\sqrt{7^{2} \times 7^{2}}\)
= 7 × 7
= 49
Number of students in the class = 49.
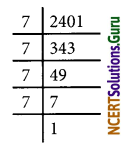
Question 8.
2025 plants are to be planted in a garden in such a way that each row contains as many plants as the number of rows. Find the number of rows and the number of plants in each row.
Solution:
Let the number of rows be x’
Number of plants in a row = x
Number of plants to be planted = x × x = x2
Given, x2 = 2025
x = √2025
= \(\sqrt{3^{4} \times 5^{2}}\)
= 32 × 5
= 9 × 5
= 45
∴ The required number of rows = 45
Also, no. of plants in a row = 45
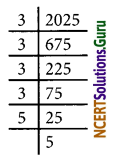
![]()
Question 9.
Find the smallest square number that is divisible by each of the numbers 4, 9, and 10.
Solution:
The least number divisible by each one of 4, 9, and 10 is their L.C.M.

∴ L.C.M = 2 × 2 × 3 × 3 × 5 = 180
Prime factors of 180 = 22 × 32 × 5
The Prime factor 5 is not in pair
180 is not a perfect square
In order to get a perfect square 180 should be multiplied by 5
The required square number = 180 × 5 = 900
Question 10.
Find the smallest square number that is divisible by each of the numbers 8, 15, and 20.
Solution:
The least number divisible by each one of 8, 15, and 20 is their L.C.M.
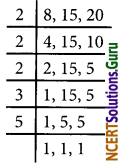
∴ L.C.M = 2 × 2 × 2 × 3 × 5 = 120
The prime factors 2, 3, and 5 are not in pairs.
∴ 120 is not a perfect square.
To get a perfect square 120 should be multiplied by 2, 3, and 5 i.e. 30.
∴ The required smallest square number = 120 × 30 = 3600