These NCERT Solutions for Class 8 Maths Chapter 11 Mensuration Ex 11.3 Questions and Answers are prepared by our highly skilled subject experts.
NCERT Solutions for Class 8 Maths Chapter 11 Mensuration Exercise 11.3
Question 1.
There are two cuboidal boxes as shown in the adjoining figure. Which box requires the lesser amount of material to make?
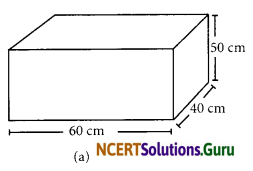
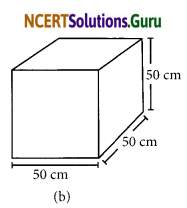
Answer:
(a) Here, l = 60 cm, b = 40 cm; h = 50 cm Total surface area of the cuboid
= 2 (lb + bh + hl)
= 2 [(60 × 40) + (40 × 50) + (50 × 60)] cm2
= 2 [2400 + 2000 + 3000] cm2
= 2 (7400) cm2 = 14800 cm2
(b) Here, l = 50 cm, b = 50 cm, h = 50 cm
Total surface area of the cuboid
= 2 (lb + bh + lh)
= 2 [(50 × 50)+ (50 × 50)+ (50 × 50)] cm2
= 2 [2500 + 2500 + 2500] cm2
= 2 × 7500 cm2 = 15000 cm2
Since, the total surface area of the second (b) is greater:
∴ Cuboid (a) will required lesser material.
![]()
Question 2.
A suitcase with measures 80 cm × 48 cm × 24 cm is to be covered with a tarpaulin cloth. How many metres of tarpaulin of width 96 cm is required to cover 100 such suitcases?
Answer:
Here, length = 80 cm, breadth = 48 cm, height = 24 cm
Total surface are a of asuitcase = 2(lb+bh+lh)
= 2[80 × 48 + 48 × 24 + 24 × 80]
= 2 [3840 + 1152 + 1920]cm2
= 2[6912] cm2 = 13824 cm2
Required tarpaulin for 100 suitcases = 13824 x 100 cm2
Width of the tarpaulin = 96 cm
Length, tarpaulin required = \(\frac{13824 \times 100}{96}\)cm
[1 m = 100 cm]
= \(\frac{13824 \times 100}{96 \times 100}\)m = \(\frac{13824}{96}\)m = 144 m
The required length of tarpaulin for 100 suitcases = 144 m
Question 3.
Find the side of a cube whose surface area is 600 cm2
Answer:
Let the side of a cube be ‘x’ cm
Total surface area of the cube = 600 cm2
6 × x2 = 600
x2 = \(\frac{600}{6}\)
x2 = 100
x2 = 102
x = 10
The required side of the cube =10 cm.
Question 4.
Rukshar painted the outside of the cabinet of measure 1m × 2m × 1.5m. How much surface area did she cover if she painted all except the bottom of the cabinet.
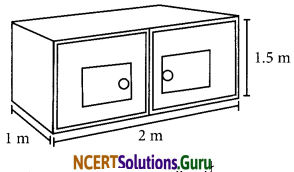
Answer:
Total surface area of the cabinet = 2 × [lb + bh + lh] sq m
Area not to be painted = Bottom of the cabinet = lb
Area to be painted = T.S.A – lb
= 2 (lb + bh + lh) – lb
= 2[1 × 2 + 2 × 1.5 + 1.5 × 1]-(1 × 2)m2
= 2(2 + 3 + 1.5) -2 m2
= 2 × 6.5 – 2 m2
= 13 – 2 m2
= 11 m2
Area to be painted = 11 m2.
![]()
Question 5.
Daniel is painting the walls and ceiling of a cuboidal hall with length, breadth and height of 15 m, 10 m and 7 m respectively. From each can of paint, 100 m2 of area is painted. How many cans of paint will she need to paint the room?
Answer:
Here l = 15 m, b = 10 m and h = 7 m.
Area to the painted = Area of four walls + Area of ceiling.
= 2 (bh + hl) + lb
2 [10 × 7 +7 × 15] + 15 × 10 m2
= 2 [70 + 105] + 150 m2
= 2(175) + 150 m2
= 350 + 150 m2 = 500 m2
= Number of cans needed = \(\frac{\text { Area to be painted }}{\text { Area painted by } 1 \text { can }}\) = \(\frac{500}{100}\) = 5
Number of cans needed = 5.
Question 6.
Describe how the two figures at the right are alike and how they are different. Which box has larger lateral surface area?
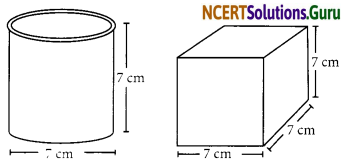
Answer:
Similarity: Both have the same height
Difference: Cylinder has curved and circular surfaces.
but in cube, all faces are identical squares
Lateral surface area of the cylinder
= 2πrh = 2 × \(\frac{22}{7}\) × \(\frac{7}{2}\) × 7 cm2
= 7 × 22 cm2 =154 cm2
Lateral surface area of the cube = 4l2 sq.m
= 4 × 7 × 7 cm2 = 196 cm2
Question 7.
A closed cylindrical tank of radius 7 m and height 3 m is made from a sheet of metal. How much sheet of metal is required?
Answer:
Here r = 7m, h = 3m
Total surface area of the cylinder = 2 π r (r + h)sq. units
= 2 × \(\frac{22}{7}\) × 7(7 + 3) = 44 × 10 m2 = 440 m2
Metal required for the tank = 440 m2.
![]()
Question 8.
The lateral surface area of a hollow cylinder is 4224 cm2. It is cut along its height and formed a rectangular sheet of width 33 cm. Find the perimeter of rectangular sheet?
Answer:
Lateral surface area of the cylinder = 4224 cm2
Let the length of the rectangular sheet be l cm
Width of the sheet = 33 cm.
Area of the rectangular sheet = L.S.A of the cylinder
l × 33 = 4224
l = \(\frac{4224}{33}\) cm = 128 cm
Perimeter of the rectangular sheet = 2 (l + b)
= 2 (128 + 33) cm = 2 × 161 cm = 322 cm
Question 9.
A road roller takes 750 complete revolutions to move once over to level a road. Find the area of the road if the diameter of a road roller is 84 cm and length is 1m.

Answer:
Radius of the roller = \(\frac{84}{2}\) = 42cm
Length of the roller = 1 m = 100 cm
Lateral surface area = 2 π rh sq unit
[road roller is a cylinder]
= 2 × \(\frac{22}{7}\) × 42 × 100 cm2
= 44 × 6 × 100 cm2 = 26400 cm2
Area levelled by 750 revolutions
= 750 × 26400 cm2
=\(\frac{750 \times 26400}{100 \times 100}\)m2 = \(\frac{75 \times 264}{10}\) = 1980 m2
![]()
Question 10.
A company packages its milk powder in cylindrical container whose base has a diameter of 14 cm and height 20 cm. Company places a label around the surface of the container (as shown in the figure). If the label is placed 2 cm from top and bottom, what is the area of the label.

Answer:
Radius of the label = \(\frac{14}{2}\) = 7 cm
Height of the label = [20 – (2 + 2)] cm
= (20 – 4) cm = 16 cm
Area of the label = Lateral surface area of the cylinder.
= 2πrh = 2 × \(\frac{22}{7}\) × 7 × 16
= 44 × 16 cm2 = 704 cm2