These NCERT Solutions for Class 8 Maths Chapter 1 Rational Numbers Ex 1.1 Questions and Answers are prepared by our highly skilled subject experts.
NCERT Solutions for Class 8 Maths Chapter 1 Rational Numbers Exercise 1.1
Question 1.
Using appropriate properties, find:
(i) \(\frac{-2}{3} \times \frac{3}{5}+\frac{5}{2}-\frac{3}{5} \times \frac{1}{6}\)
(ii) \(\frac{2}{5} \times\left(\frac{-3}{7}\right)-\frac{1}{6} \times \frac{3}{2}+\frac{1}{14} \times \frac{2}{5}\)
Solution:


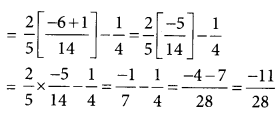
Question 2.
Write the additive inverse of each of the following:
(i) \(\frac{2}{8}\)
(ii) \(\frac{-5}{9}\)
(iii) \(\frac{-6}{-5}\)
(iv) \(\frac{2}{-9}\)
(v) \(\frac{19}{-6}\)
Solution:
(i) Additive inverse of \(\frac{2}{8}\) is \(\frac{-2}{8}\)
(ii) Additive inverse of \(\frac{-5}{9}\) is \(\frac{5}{9}\)
(iii) Additive inverse of \(\frac{-6}{-5}\) is \(\frac{-6}{5}\)
(iv) Additive inverse of \(\frac{2}{-9}=\left(\frac{-2}{9}\right)\) is \(\frac{2}{9}\)
(v) Additive inverse of \(\frac{19}{-6}=\left(\frac{-19}{6}\right)\) is \(\frac{19}{6}\)
![]()
Question 3.
Verify that -(-x) = x for:
(i) x = \(\frac{11}{15}\)
(ii) x = \(\frac{-13}{17}\)
Solution:
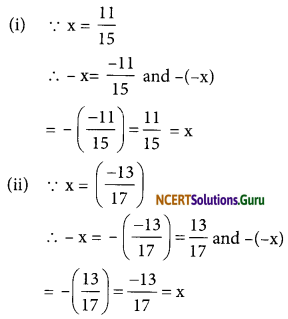
Question 4.
Find the multiplicative inverse of the following:
(i) -13
(ii) \(\frac{-13}{19}\)
(iii) \(\frac{1}{5}\)
(iv) \(\frac{-5}{8} \times \frac{-3}{7}\)
(v) \(-1 \times \frac{-2}{5}\)
(vi) -1
Solution:
(i) Multiplicative inverse of -13 is \(\frac{-1}{13}\)
(ii) Multiplicative inverse of \(\frac{-13}{19}\) is \(\frac{-19}{13}\)
(iii) Multiplicative inverse of \(\frac{1}{5}\) is 5.
(iv) \(\left(\frac{-5}{8} \times \frac{-3}{7}\right)=\frac{(-5) \times(-3)}{8 \times 7}=\frac{56}{15}\)
Multiplicative inverse of \(\frac{-5}{8} \times \frac{-3}{7}\) is \(\frac{15}{56}\)
(v) \(-1 \times \frac{-2}{5}=\frac{(-1) \times(-2)}{5}=\frac{2}{5}\)
Multiplicative inverse of \(-1 \times \frac{-2}{5}\) is \(\frac{5}{2}\)
(vi) Multiplicative inverse of -1 is -1.
![]()
Question 5.
Name the property under multiplication used in each of the following:
(i) \(\frac{-4}{5} \times 1=1 \times \frac{-4}{5}=\frac{-4}{5}\)
(ii) \(\frac{-13}{17} \times \frac{-2}{7}=\frac{-2}{7} \times \frac{-13}{17}\)
(iii) \(\frac{-19}{29} \times \frac{29}{-19}=1\)
Solution:
(i) \(\frac{-4}{5} \times 1=1 \times \frac{-4}{5}=\frac{-4}{5}\)
1 is the multiplicative identity.
(ii) \(\frac{-13}{17} \times \frac{-2}{7}=\frac{-2}{7} \times \frac{-13}{17}\)
Multiplication is commutative.
(iii) \(\frac{-19}{29} \times \frac{29}{-19}=1\)
Multiplicative inverse.
Question 6.
Multiply \(\frac{6}{13}\) by the reciprocal of \(\frac{-7}{16}\).
Solution:
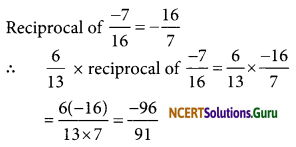
Question 7.
Tell what property allows you to compute \(\frac{1}{3} \times\left(6 \times \frac{4}{3}\right) \text { as }\left(\frac{1}{3} \times 6\right) \times \frac{4}{3}\)
Solution:
\(\frac{1}{3} \times\left(6 \times \frac{4}{3}\right) \text { as }\left(\frac{1}{3} \times 6\right) \times \frac{4}{3}\)
In the given question, we use the associative property.
![]()
Question 8.
Is \(\frac{8}{9}\) the multiplicative inverse of -1\(\frac{1}{8}\)? Why or why not?
Solution:
\(\frac{8}{9} \times-\frac{9}{8}=-1\) but is not equal to 1.
So, \(\frac{8}{9}\) is not the multiplicative inverse of -1\(\frac{1}{8}\)
Question 9.
Is 0.3 the multiplicative inverse of 3\(\frac{1}{3}\)? Why or why not?
Solution:
0.3 = \(\frac{3}{10}\)
3\(\frac{1}{3}\) = \(\frac{10}{3}\)
\(\frac{3}{10} \times \frac{10}{3}=1\)
∴ Multiplicative inverse of 3\(\frac{1}{3}\) is 0.3.
Question 10.
Write:
(i) The rational number that does not have a reciprocal.
(ii) The rational numbers that are equal to their reciprocals.
(iii) The rational number that is equal to its negative.
Solution:
(i) The rational number ‘0’ does not have a reciprocal.
(ii) The rational numbers 1 and (-1) are equal to their reciprocal.
(iii) The rational number ‘0’ is equal to its negative [(0) + (0) = 0]
∴ The negative of 0 is 0.
![]()
Question 11.
Fill in the blanks:
(i) Zero has ________ reciprocal.
(ii) The numbers ________ and ________ are their own reciprocals.
(iii) The reciprocal of -5 is ________
(iv) Reciprocal of \(\frac{1}{\mathrm{x}}\) when x ≠ 0 is ________
(v) The product of two rational numbers is always a ________
(vi) The reciprocal of a positive rational number is ________
Solution:
(i) no
(ii) 1 and -1
(iii) \(\frac{-1}{5}\)
(iv) x
(v) rational number
(vi) positive