These NCERT Solutions for Class 7 Maths Chapter 6 The Triangles and Its Properties InText Questions and Answers are prepared by our highly skilled subject experts.
NCERT Solutions for Class 7 Maths Chapter 6 The Triangles and Its Properties InText Questions
NCERT In-text Question Page No. 113 & 114
Question 1.
Write the six elements (i.e. the 3 sides and the 3 angles) of ΔABC.
Answer:
Six elements of ΔABC are: ∠A, ∠B, ∠C, \(\overline{\mathrm{AB}}\), \(\overline{\mathrm{BC}}\), and \(\overline{\mathrm{CA}}\).
Question 2.
Write the:
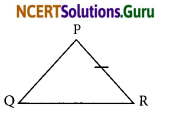
(i) Side opposite to the vertex Q of ΔPQR
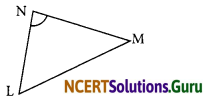
(ii) Angle opposite to the side LM of ΔLMN
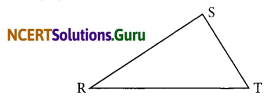
(iii) Vertex opposite to the side RT of ΔRST
Answer:
(i) The side opposite to the vertex Q is \(\overline{\mathrm{PR}}\).
(ii) The angle opposite to the side LM is ∠N.
(iii) Vertex opposite to the side RT is ‘S’.
![]()
Question 3.
Look at figures and classify each of the triangles according to its.
(a) Sides
(b) Angles
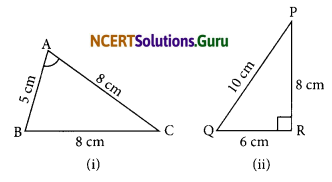
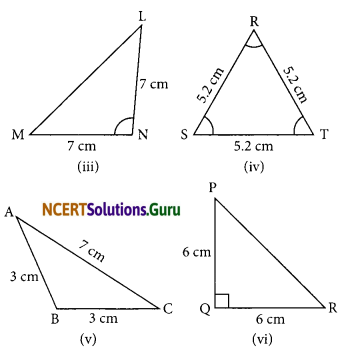
Answer:
(i) (a) Since \(\overline{\mathrm{AC}}=\overline{\mathrm{BC}}\) = 8 cm
∴ ΔABC is an isosceles triangle,
(b) Since all angles of ∴ABC are less than 90°.
∴ It is an acute triangle.
(ii) (a) Since PQ ≠ QR ≠ RP
∴ ΔPQR is a scalene triangle.
(b) Since ∠R = 90°
∴ ΔPRQ is a right triangle.
(iii) (a) In ΔLMN, LN = MN = 7 cm
∴ ΔLMN is an isosceles triangle,
(b) In ΔLMN, ∠N > 90°
∴ ΔLMN is an obtuse triangle.
(iv) (a) In ΔRST, RS = ST = TR = 5.2 cm
∴ It is an equilateral triangle.
(b) All the angles of ΔRST are acute.
∴ It is an acute triangle.
(v) (a) In ΔABC, \(\overline{\mathrm{AB}}=\overline{\mathrm{BC}}\) = 3 cm
∴ It is an isosceles triangle.
(b) In ΔABC, ∠B > 90°
∴ It is an obtuse triangle.
(vi) (a) In ΔPQR, latex]\overline{\mathrm{PQ}}=\overline{\mathrm{QR}}[/latex] = 6 cm
∴ It is an isosceles triangle.
(b) In ΔPQR, ∠Q = 90°
∴ It is a right triangle.
![]()
NCERT In-text Question Page No. 118
Question 1.
An exterior angle of a triangle is of measure 70° and one of its interior opposite angles is for measure 25°. Find the measure of the other interior opposite angle.
Answer:
Exterior angle = 70°
Interior opposite angles are 25° and x.
∴ x + 25° = 70°
[Using the exterior angle property of a triangle]
or x = 70°- 25°= 45°
∴ The required interior opposite angle = 45°.
Question 2.
The two interior opposite angles of an exterior angle of triangle are 60° and 80°. Find the measure of the exterior angle.
Answer:
Interior angles are 60° and 80°.
∵ [Exterior angle] = 60° + 80° = 140°
Question 3.
Is something wrong in this diagram?
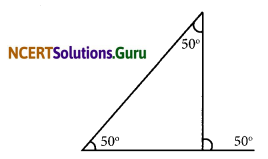
Answer:
We know that an exterior angle of a triangle is equal to the sum of interior opposite angles. Here interior angles are 50° each and exterior angle is 50°.
∴ This triangle cannot be formed.
[∵ 50° ≠ 50° + 50°]
![]()
NCERT In-text Question Page No. 122
Question 1.
Two angles of a triangle are 30° and 80°. Find the third angle.
Answer:
Let the third angle be x.
∴ Using the angle sum property of a triangle,
30° + 80° + x = 180°
or x + 110° = 180°
or x = 180°- 110° = 70°
∴ The measure of the required third angle is 70°.
Question 2.
One of the angles of a triangle is 80° and the other two angles are equal. Find the measure of each of the equal angles.
Answer:
Let each of the equal angles be x
x + x + 80° = 180°
(angle sum property of a triangle)
2x + 80° = 180°
2x = 180° – 80°
2x = 100°
x = \(\frac{100^{\circ}}{2}\) = 50°
∴ The required measure of each of the equal angle is 50°.
Question 3.
The three angles of a triangle are in the ratio 1:2:1. Find all the angles of the triangle. Classify the triangle in two different ways.
Answer:
Let the three angles of a triangle be x, 2x and x
x + 2x + x = 180°
(using the angle sum property)
2x + 2x = 180°
4x = 180°
x \(\frac{180^{\circ}}{4}\) = 45°
Thus, the three angles are 45°, 90° and 45°. It is an isosceles triangle (two angles are equal, opposite sides also equal)
As one angle is 90°.
∴ It is a right-angled triangle.
![]()
NCERT In-text Question Page No. 123 & 124
Question 1.
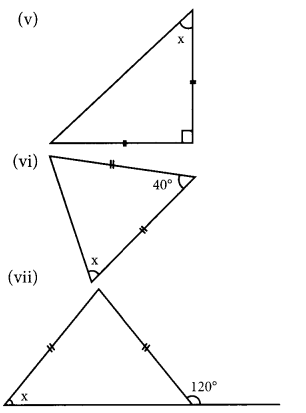
Find angle x in each figure:
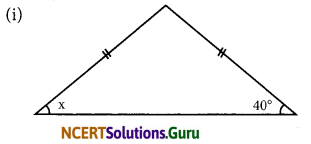
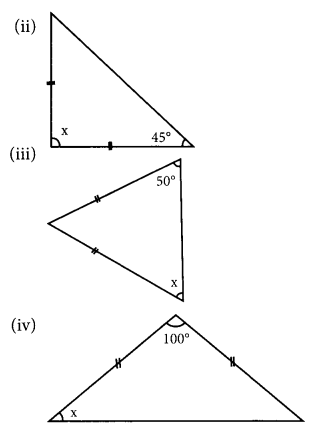
Answer:
(i) Since the two sides in the triangle are equal, the base angle opposite to equal sides are equal.
∴ x = 40°
(ii) Since the two sides of the triangle are equal, the base angles opposite to equal sides are equal so, the other angle = 45°
Sum of three angles of a triangle = 180°
45° + 45° + x = 180°
x + 90° = 180°
x = 180° – 90°
x = 90°
(iii) Since the two sides of the triangle are equal, the base angles opposite to equal sides are equal.
x = 50°
(iv) Base angles opposite to the equal sides of an isosceles triangle are equal and the sum of the measures of the three angles is 180°.
100° + x + x = 180°
2x = 180° – 100°
2x = 80°
x = \(\frac{80^{\circ}}{2}\) = 40°
(v) Base angles opposite to the equal sides of an isosceles triangles are equal and the sum of the measure of three angles of triangle is 180°.
x + x + 90° = 180°
2x + 90° = 180°
2x = 180° – 90°
2x = 90°
x = \(\frac{90^{\circ}}{2}\) = 45°
(vi) Base angles opposite to the equal sides of an isosceles triangle are equal and the sum of the measures of the three angles of triangle is 180°.
x + x + 40° = 180°
2x + 40° = 180°
2x = 180° – 40°
2x = 140°
x = \(\frac{140^{\circ}}{2}\)
= 70°
x = 70°
(vii) In the figure, two sides of the triangle are equal.
∴ The base angles opposite to equal sides are equal one of the base angle = x
other base angle = x
Now, x° and 120° form a linear pair = 180°
x + 120° = 180°
x = 180° -120°
= 60°
Thus, the value of x = 60°
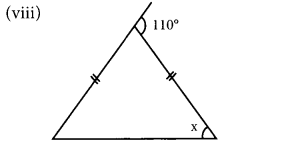
(viii) In the figure, two sides of the triangle are equal.
since, one of the base angles = x
∴ The other base angle = x
Since, exterior angle is equal to sum of the interior opposite angles
∴ x + x = 110°
2x = 110°
x = \(\frac{110^{\circ}}{2}\) = 55°
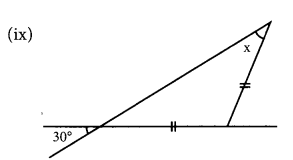
(ix) Two sides of the triangle are equal.
∴ The base angles opposite to the equal sides are equal.
Since, one of the base angle = x
∴ The other base angle = x
Also, the vertically opposite angles 30° and x are equal.
∴ x = 30°
![]()
Question 2.
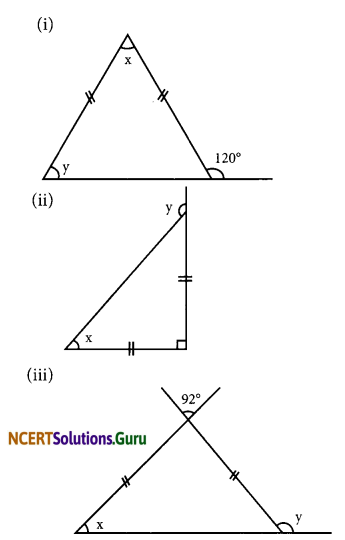
Find angles x and y in each figure.
Answer:
(i) Two sides of the triangle are equal.
∴ The base angles opposite to the equal sides are equal.
The other base angle is y.
Now y and 120° form a linear pair.
∴ y + 120° = 180°
y = 180° – 120° = 60°
∴ x + y + y = 180°
(sum of the three angles = 180°)
x + 60° + 60°= 180°
x+ 120° = 180°
x = 180° – 120°
= 60°
Thus x = 60° and y = 60°
(ii) Two sides of a triangles are equal.
∴ The base angles opposite to equal sides are equal. Since one of the base angle is ‘x’
∴ The other base angle = x
The given triangle is a right-angled triangle.
x + x + 90° = 180°
2x + 90° = 180°
2x = 180° – 90°
2x = 90°
x = \(\frac{90^{\circ}}{2}\) = 45°
Now x and y form a linear pair
x + y = 180°
45°+ y = 180°
y = 180° – 45° = 135°
Thus, x = 45° and y = 135°
(iii) In the given figure, two sides of a triangle are equal.
∴ The base angles are x and x
The third angle = 92°
(vertically opposite angles are equal)
x + x + 92° = 180°
(Sum of the three angles of a triangle is 180°)
2x + 92° = 180°
2x = 180° – 92°
2x = 88°
x = \(\frac{88^{\circ}}{2}\) = 44°
Now, x and y form a linear pair
x + y = 180°
44 + y = 180°
y = 180° – 44° = 136°
Thus, x = 44° and y = 136°
![]()
NCERT In-text Question Page No. 129 & 130
Question 1.
Find the unknown length x in the following figures.
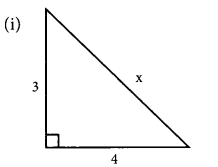
(i) In the given right-angled triangle, the longest side (hypotenuse) is x
x2 = 32 + 42
(using pythagoras property)
= 9 + 16
= 25
or x2 = 52
x = \(\sqrt{25}\)
= 5
x = 5
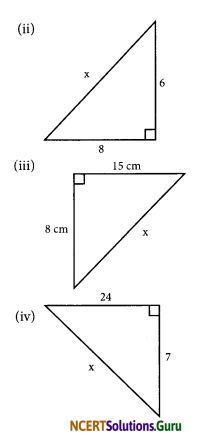
(ii) The given figure is a right-angled triangle.
x2 = 62 + 82
(using pythagoras property)
= 36 + 64
x2 = 100
x2 = 102
∴ x = 10
(iii) The given figure is a right-angled triangle.
x2 = 82 + 152
(using pythagoras property)
x2 = 64 + 225
x2 = 289
x2 = 172
x = 17
(iv) The given figure is a right-angled triangle
x2 = 72 + 242
(using pythagoras property)
x2 = 49 + 576
x2 = 625
x2 = 252
x = 25
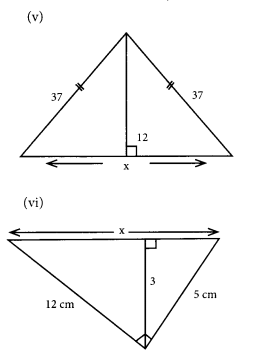
(v) The given figure can be labelled as ΔABC and the altitude is AD. Consider the right-angled triangle ABD
AB2 = AD2 + BD2
(using pythagoras property)
372 = 122 + BD2
1369 = 144 + BD2
1369 – 144 = BD2
1225 = BD2
352 = BD2
∵ BD = 35
In the right-angled triangle ADC
AC2 = AD2 + DC2
(using pythagoras property)
372 = 122 + DC2
1369 = 144 +DC2
1369 – 144 = DC2
1225 = DC2
352 = DC2
∴ DC = 35
∵ BC = BD + DC
= 35 + 35
x = 70
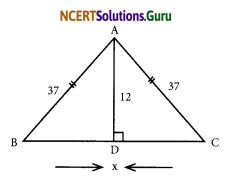
(vi) In the given right-angled triangle
x2 = 122 + 52
(using the pythagoras property)
= 144 + 25
x2 = 169
x2 = 132
∴ x = 13