These NCERT Solutions for Class 6 Maths Chapter 6 Integers InText Questions and Answers are prepared by our highly skilled subject experts.
NCERT Solutions for Class 6 Maths Chapter 6 Integers InText Questions
![]()
NCERT In-text Question Page No. 116
Question 1.
Write the following numbers with appropriate signs:
(a) 100 m below sea level.
(b) 25°C above 0°C temperature.
(c) 15°C above 0°C temperature.
(d) Any five numbers less than 0.
Answer:
(a) 100m below sea level → -100 m
(b) 25°C above 0°C temperature → + 25°C
(c) 15°C below 0°C temperature → -15°C
(d) Five numbers less than 0: {-1, -3, -10, -25, -105}
Note:
(i) If profit is represented by ‘+’ sign, then loss may be represented by sign.
(ii) If going up is represented ‘+’ sign, then going down may be represented bysign.
(iii) If earnings are represented by Vsign, sign, then withdrawal is sign. then spending may be represented by sign.
(iv) If temperature above 0° is ‘+’ sign, then temperature below 0° may be represented by ‘-‘ sign.
(v) If depositing money to bank is ‘+’
NCERT In-text Question Page No. 118
Question 1.
Mark 3, 7, -4, -8, -8, -1 and -3 on the number line.
Answer:
Given numbers are marked on the number line as shown below:

The integer -8 is at A
The integer -4 is at B
The integer -3 is at C
The integer -1 is at D
The integer 3 is at E
The integer 7 is at F
Note : Look at the number line given here. We find that for every integer to the right of zero there is a corresponding integer to the left of zero (at the same distance from zero but with a negative sign). Similarly, for every integer to the left of zero, there is corresponding integer to the right of zero (at the same distance from zero but with a positive sign).
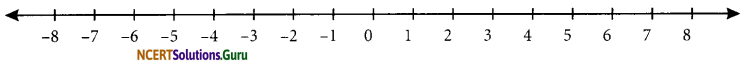
NCERT In-text Question Page No. 119
Question 1.
Compare the following pairs of number using > or <.

Answer:

From the above exercise, Rohini arrived at the following conclusions :
(a) Every positive integer is larger than every negative integer.
(b) Zero is less than every positive integer.
(c) Zero is larger than every negative integer.
(d) Zero is neither a negative integer nor a positive integer.
(e) Farther a number from zero on the right, larger is its value.
(f) Farther a number from zero on the left, smaller is its value.
Do you agree with her? Give examples.
Answer:
a. True
b. True
c. True
d. True
e. True
f. True
NCERT In-text Question Page No. 123
Question 1.
Draw a figure on the ground in the form of a horizontal number line as shown below: Frame questions as given in the said example and ask your friends.

Answer:
Do it yourself.
NCERT In-text Question Page No. 125
Question 2.
Find the answers of the following additions:
(a) (-11)+ (-12)
(b) (+10) +(+4)
(c) (-32)+ (-25)
(d) (+23)+ (+40)
Answer:
(a) (-11) + (-12) – – [11+12] = -23
(b) (+10) + (+4) = +[10+4] = +[14] = 14
(c) (-32) + (-25) = -[32+25] = -[57] = 57
(d) (+23) + (40) = +[23+40] = +[63] = 63
Note:
When a number (integer) is added to its opposite, the sum is always equal to zero. Such two integers are also called the ADDITIVE INVERSE of each other.
Question 3.
Find the solution of the following:
(a) (-7) +(-8)
(b) (-9)+ (+13)
(c) (+7)+ (-10)
(d) (+12) +(-7)
Answer:
(a) (-7) + (+8):
∵ Opposite of (-7) is (+7) and (+8)
= (+7) + (+1)
∴ (-7) + (+8) = (-7) + (+7) + (+1)
= 0 + (+1) [∵ (-7) + (+7) = 0] = +1 =1
(b) (-9)+ (-13):
∵ (+13)=(+9)+(+4)
∴ (-9) + (+13) = (-9) + (+9) + (+4)
= 0 + (+4) [∵ (-9) + (+9) = 0]
= +4 = 4
(c) (+7)+ (-10):
∵ (-10) = (-7)+(-3)
∴ (+7) + (-10) = (+7) + (-7) + (-3)
= 0 + (-3) [∵ (+7) + (-7) = 0]
= -3
(d) (+12) +(-7):
∵ (+12) = (+7) + (+5)
∴ (+12) + (-7) = (+7) + (+5) + (-7)
= 0 + (-3) [∵ (+7) + (-7) = 0]
= 5
NCERT In-text Question Page No. 127
Question 1.
Find the solution of the following additions using a number line.
(a) (-2)+ 6
(b) (-6)+ 2
Make two such questions and solve them using the number line.
Answer:
(a) (-2) + 6
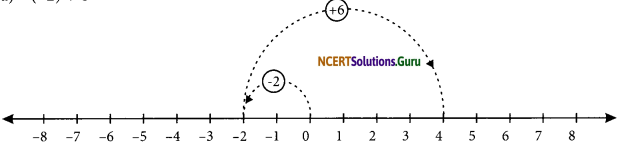
First move 2 steps to the left of 0 to reach at -2. From here, move 6 steps to the right of -2, to reach at 4.
(-2) + (+6) = +4
(b) (-6)+ 2
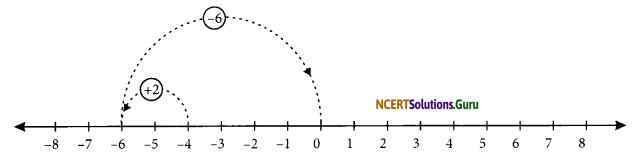
On the number line, we first move 6 equal steps (each of 1 unit) to the left of 0, to reach at (6). Now move 2 steps to the right of (-6) to reach at (-4).
∴ (-6) + (+2) = -4
Question 2.
Find the solution of the following without using number line:
(a) (+7)+ (-11)
(b) (-13)+ (+10)
(c) (-7) +(+9)
(d) (+10) +(-5)
Make five such questions and solve them.
Answer:
(a) (+7) + (-11)
∵ (-11) = (-7) +(-4)
∴ (+7) + (-11) = (+7) + (-7) + (-4) = 0 + (-4)
[∵ (+7) + (-7) = 0] = -4
Thus, (+7) + (-11) = -4
(b) (-13) + (+10):
∵ (-13)=(-10)+(-3)
∴ (-3) +(+10) = (-10) +(-3)+ (+10)
= (-10) + (+10) + (-3)
= 0 + (-3) = -3 [∵ (-10) + (+10) = 0]
Thus, (-13) + (+10) = -3
(c) (-7) + (+9):
∵ (+9) = (+7) + (+2)
∴ (-7) + (+9) = (-7) + (+2) = 0 + (+2)
[∵ (-7) + (+7) = 0]
= +2
Thus, ( – 7) + (+9) = +2
(d) (+10) +(-5):
∵ (+10) = (+5) + (+5)
∴ (+10) + (-5) = (+5) + (+5) + (5) = +5 + 0
[∵ (+5) + (-5) = 0]
= +5
Thus, (+10) +(-5) = (+5)