These NCERT Solutions for Class 6 Maths Chapter 14 Practical Geometry Ex 14.6 Questions and Answers are prepared by our highly skilled subject experts.
NCERT Solutions for Class 6 Maths Chapter 14 Practical Geometry Exercise 14.6
Question 1.
Draw ∠POQ of measure 75° and find its line of symmetry.
Answer:
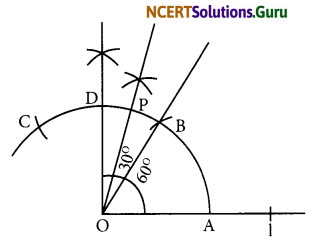
Steps of construction:
(a) Draw a line l and mark a point O on it.
(b) Place the pointer of the compasses at O and draw an arc of any radius which intersects the line l at A.
(c) Taking same radius, with centre A, cut the previous arc at B.
(d) Join OB, then ∠BOA = 60 .
(e) Taking same radius, with centre B, cut the previous arc at C.
(f) Draw bisector of ∠BOC. The angle is of 90 . Mark it at D. Thus, ∠DOA = 90°
(g) Draw \(\overline{\mathrm{OP}}\) as bisector of ∠DOB. Thus, ∠POA = 75°
![]()
Question 2.
Draw an angle of measure 147° and construct its bisector.
Answer:
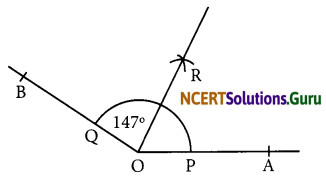
Steps of construction:
(a) Draw a ray \(\overline{\mathrm{OA}}\) .
(b) With the help of protractor, construct ∠AOB = 147°
(c) Taking centre O and any convenient radius, draw an arc which intersects the arms \(\overline{\mathrm{OA}}\) and \(\overline{\mathrm{OB}}\) at P and Q respectively.
(d) Taking P as centre and radius more than half of PQ, draw an arc.
(e) Taking Q as centre and with the same radius, draw another arc which intersects the previous at R.
(f) Join OR and produce it.
(g) Thus, \(\overline{\mathrm{OR}}\) is the required bisector of ∠AOB.
Question 3.
Draw a right angle and construct its bisector.
Answer:
Steps of construction:
(a) Draw a line PQ and take a point O on it.
(b) Taking O as centre and convenient radius, draw an arc which intersects PQ at A and B.
(c) Taking A and B as centres and radius more than half of AB, draw two arcs which intersect each other at C.
(d) Join OC. Thus, ∠COQ is the required right angle.
(e) Taking B and E as centre and radius more than half of BE, draw two arcs which intersect each other at the point D.
(f) Join OD. Thus, \(\overline{\mathrm{OD}}\) is the required bisector of ∠COQ.
![]()
Question 4.
Draw an angle of measure 153° and divide it into four equal parts.
Answer:
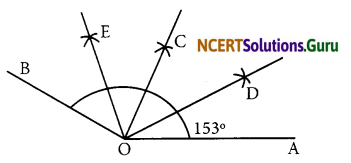
Steps of construction:
(a) Draw a ray \(\overline{\mathrm{OA}}\)
(b) At O, with the help of a protractor, construct ∠AOB = 153°.
(c) Draw \(\overline{\mathrm{OC}}\) as the bisector of ∠AOB.
(d) Again, draw \(\overline{\mathrm{OD}}\) as bisector of ∠AOC.
(e) Again, draw \(\overline{\mathrm{OE}}\) as bisector of ∠BOC.
(f) Thus, \(\overline{\mathrm{OC}}\), \(\overline{\mathrm{OD}}\) and \(\overline{\mathrm{OE}}\) divide ∠AOB in four equal arts.
Question 5.
Construct with ruler and compasses, angles of following measures:
(a) 60°
(b) 30°
(c) 90°
(d) 120°
(e) 45°
(f) 135°
Answer:
Steps of construction:
(a) 60°
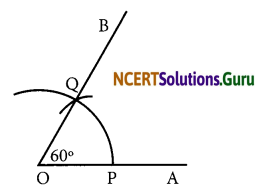
(i) Draw a ray \(\overline{\mathrm{OA}}\).
(ii) Taking O as centre and convenient radius, mark an arc, which intersects \(\overline{\mathrm{OA}}\) at P.
(iii) Taking P as centre and same radius, cut previous arc at Q.
(iv) Join OQ.
Thus, ∠BOA is required angle of 60°.
(b) 30°
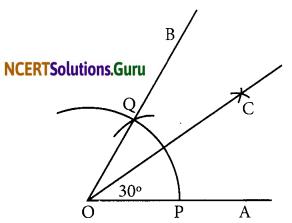
(i) Draw a ray \(\overline{\mathrm{OA}}\) .
(ii) Taking O as centre and convenient radius, mark an arc, which intersects \(\overline{\mathrm{OA}}\) at P.
(iii) Taking P as centre and same radius, cut previous arc at Q.
(iv) Join OQ. Thus, ∠BOA is required angle of 60°.
(v) Put the pointer on P and mark an arc.
(vi) Put the pointer on Q and with same radius, cut the previous arc at C. Thus, ∠COA is required angle of 30°.
(c) 90°
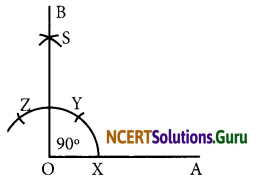
- Draw a ray \(\overline{\mathrm{OA}}\).
- Taking O as centre and convenient radius, mark an arc, which intersects \(\overline{\mathrm{OA}}\) at X.
- Taking X as centre and same radius, cut previous arc at Y.
- Taking Y as centre and same radius, draw another arc intersecting the same arc at Z.
- Taking Y and Z as centres and same radius, draw two arcs intersecting each other at S.
- Join OS and produce it to form a ray OB.
Thus, ∠BOA is required angle of 90.
![]()
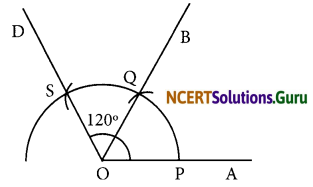
(d) 120°
- Draw a ray \(\overline{\mathrm{OA}}\).
- Taking O as centre and convenient radius, mark an arc, which intersects \(\overline{\mathrm{OA}}\) at P.
- Taking P as centre and same radius, cut previous arc at Q.
- Taking Q as centre and same radius cut the arc at S.
- Join OS.
Thus, ∠AOD is required angle of 120°.
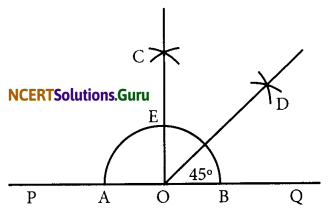
(e) 45°
- Draw a ray \(\overline{\mathrm{OA}}\) .
- Taking O as centre and convenient radius, mark an arc, which intersects \(\overline{\mathrm{OA}}\) at X.
- Taking X as centre and same radius, cut previous arc at Y.
- Taking Y as centre and same radius, draw another arc intersecting the same arc at Z.
- Taking Y and Z as centres and same radius, draw two arcs intersecting each other at S.
- Join OS and produce it to form a ray OB. Thus, ∠BOA is required angle of 90°.
- Draw the bisector of ∠BOA.
Thus, ∠MOA is required angle of 45°.
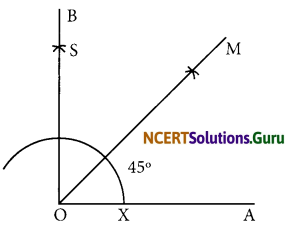
(f) 135°
- Draw a line PQ and take a point O on it.
- Taking O as centre and convenient radius, mark an arc, which intersects PQ at A and B.
- Taking A and B as centres and radius more than half of AB, draw two arcs intersecting each other at R.
- Join OR. Thus, ∠QOR = ∠POQ = 90° .
- Draw OD the bisector of ∠POR.
Thus, ∠QOD is required angle of 135°.
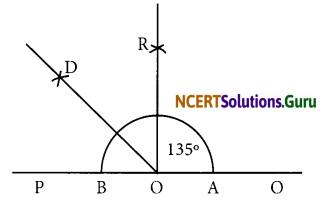
![]()
Question 6.
Draw an angle of measure 45° and bisect it.
Answer:
Steps of construction:
(a) Draw a line PQ and take a point O on it.
(b) Taking O as centre and a convenient radius, draw an arc which intersects PQ at two points A and B.
(c) Taking A and B as centres and radius more than half of AB, draw two arcs which intersect each other at C.
(d) Join OC. Then ∠COQ is an angle of 90.
(e) Draw \(\overline{\mathrm{OE}}\) as the bisector of ∠COE. Thus, ∠QOE = 45°
(f) Again draw \(\overline{\mathrm{OG}}\) as the bisector of ∠QOE.
Thus, ∠QOG = ∠EOG = 22\(\frac { 1 }{ 2 }\)°
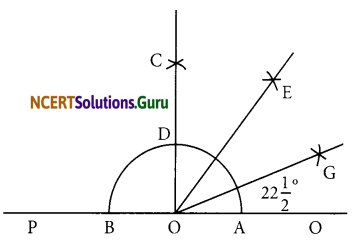
Question 7.
Draw an angle of measure 135° and bisect it.
Answer:
Steps of construction:
(a) Draw a line PQ and take a point O on it.
(b) Taking O as centre and convenient radius, mark an arc, which intersects PQ at A and B.
(c) Taking A and B as centres and radius more than half of AB, draw two arcs intersecting each other at R.
(d) Join OR. Thus, ∠QOR = ∠POQ = 90°.
(e) Draw \(\overline{\mathrm{OD}}\) the bisector of ∠POR.
Thus, ∠QOD is required angle of 135°.
(f) Now, draw \(\overline{\mathrm{OE}}\) as the bisector of ∠QOD.
Thus, ∠QOE = ∠DOE =67\(\frac { 1 }{ 2 }\)°
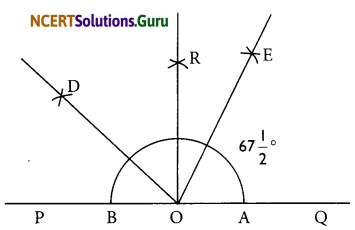
![]()
Question 8.
Draw an angle of 70°. Make a copy of it using only a straight edge and compasses.
Answer:
Steps of construction:
Step I: Draw a line 1 and mark a point O on it.
Step II: Using a protractor construct ∠AOB = 70°.
Step III: With centre O and a suitable radius, draw an arc which intersects \(\overline{\mathrm{OA}}\) and \(\overline{\mathrm{OB}}\) at E and F respectively.
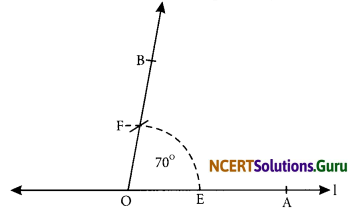
Step IV: Draw a ray \(\overline{\mathrm{PQ}}\).
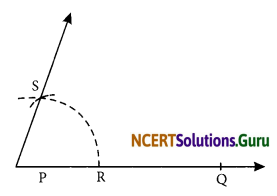
Step V: Keeping the same radius and centre P, draw an arc intersecting \(\overline{\mathrm{PQ}}\) at R.
Step VI: With centre R and radius equal to EF, draw an arc intersecting the previous arc at S.
Step VII: Join PS and produce it.
Question 9.
Draw an angle of 40° Copy its supplementary angle.
Answer:
Steps of construction:
Step I: (a) By using protractor draw ∠AOB = 40°
∠COF is the supplementary angle.
Step II: With centre O and a convenient radius, draw an arc which intersects \(\overline{\mathrm{OC}}\) and \(\overline{\mathrm{OB}}\) and E and F respectively.
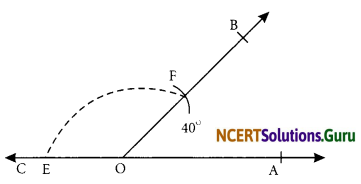
Step III: Draw a ray \(\overline{\mathrm{OC}}\).
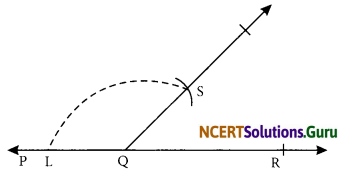
Step IV: With centre Q and same radius, draw an arc intersecting \(\overline{\mathrm{OC}}\) at L.
Step V: With centre L and radius equal to EF draw an arc which intersects the previous arc at S.
Step VI: Join QS and produce it.
Thus, ZPQS is the copy of the supplementary angle ZCOB.