These NCERT Solutions for Class 6 Maths Chapter 11 Algebra Ex 11.5 Questions and Answers are prepared by our highly skilled subject experts.
NCERT Solutions for Class 6 Maths Chapter 11 Algebra Exercise 11.5
Question 1.
State which of the following are equations (with a variable). Give reason for your answer. Identify the variable from the equations with a variable.
(a) 17 = x + 7
(b) (t – 7) > 5
(c) \(\frac{4}{2}\) = 2
(d) (7 × 3) – 19 = 8
(e) 5 × 4 – 8 = 2x
(f) x – 2 = 0
(g) 2m < 30
(h) 2n + 1 = 11
(i) 7 = (11 × 5) – (12 × 4)
(j) 7 = (11 × 2) + p
(k) 20 = 5y
(l) \(\frac{3 \mathrm{q}}{2}\) < 5
(m) z + 12 > 24
(n) 20 – (10 – 5) = 3 × 5
(o) 7 – x = 5
Answer:
(a) It is an equation of variable as both the sides are equal. The variable is x.
(b) It is not an equation as L.H.S. is greater than R.H.S.
(c) It is an equation with no variable. But it is a false equation.
(d) It is an equation with no variable. But it is a false equation.
(e) It is an equation of variable as both the sides are equal. The variable is x.
(f) It is an equation of variable x.
(g) It is not an equation as L.H.S. is less than R.H.S.
(h) It is an equation of variable as both the sides are equal. The variable is n.
(i) It is an equation with no variable as its both sides are equal.
(j) It is an equation of variable p.
(k) It is an equation of variable y.
(l) It is not an equation as L.H.S. is less than R.H.S.
(m) It is not an equation as L.H.S. is greater than R.H.S.
(n) It is an equation with no variable.
(o) It is an equation of variable x
![]()
Question 2.
Complete the entries in the third column of the table.
| Equation | Value of variable | Equation satisfied Yes/No |
| (a) 10y = 80 | y = 10 | – |
| (b) 10y = 80 | y = 8 | – |
| (c) 10y = 80 | y = 5 | – |
| (d) 4l = 20 | l = 20 | – |
| (e) 4l = 20 | l = 80 | – |
| (f) 4l = 20 | l = 5 | – |
| (g) b + 5 = 9 | b = 5 | – |
| (h) b + 5 = 9 | b = 9 | – |
| (i) b + 5 = 9 | b = 4 | – |
| (j) h – 8 = 5 | h = 13 | – |
| (k) h – 8 = 5 | h = 8 | – |
| (l) h – 8 = 5 | h = 0 | – |
| (m) p + 3 = 1 | P = 3 | – |
| (n) p + 3 = 1 | P = 1 | – |
| (o) p + 3 = 1 | P = 0 | – |
| (p) p + 3 = 1 | P = -1 | |
| (q) p + 3 = 1 | P = -2 | – |
Answer:
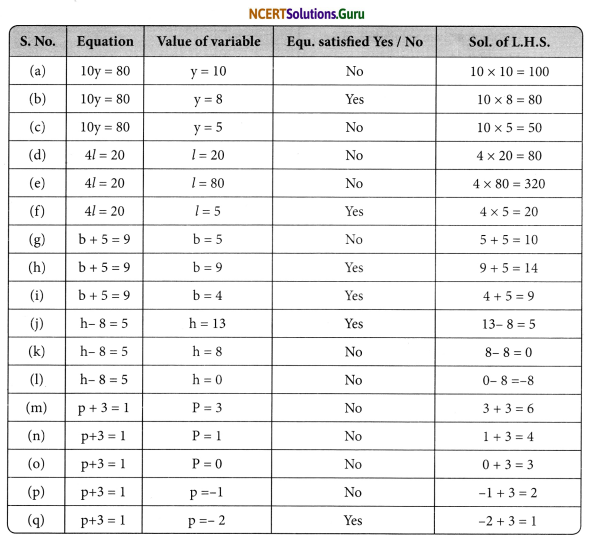
![]()
Question 3.
Pick out the solution from the values given in the bracket next to each equation. Show that the other values do not satisfy the equation.
(a) 5m = 60 (10,5,12,15)
(b) n + 12= 20(12,8,20,0)
(c) p – 5 = 5 (0, 10, 5,-5)
(d) \(\frac{\mathrm{q}}{2}\) = 7 (7, 2, 10, 14)
(e) r – 4 = 0 (4,-4, 8,0)
(f) x + 4 = 2 (-2, 0, 2, 4)
Answer:
(a) 5m = 60
Putting the given values in L.H.S.,
5 × 10 = 50
∵ L.H.S. ≠ R.H.S
∴ m = 10 is not the solution
5 × 5 = 25
∵ L.H.S. ≠ R.H.S
∴ m = 5 is not the solution
5 × 12 = 60
∵ L.H.S. = R.H.S
∴ m = 12 is a solution
5 × 15 = 75
∵ L.H.S. ≠ R.H.S
∴ m = 15 is not the solution
(b) n + 12 = 20
Putting the given values in L.H.S.,
12 + 12 = 24
∵ L.H.S. ≠ R.H.S
∴ n = 12 is not the solution
8 + 12 = 20
∵ L.H.S. = R.H.S
∴ n = 8 is a solution
20 + 12 = 32
∵ L.H.S. ≠ R.H.S
∴ n = 20 is not the solution
0 + 12 = 12
∵ L.H.S. ≠ R.H.S
∴ n = 0 is not the solution
(c) p – 5 = 5
Putting the given values in L.H.S.,
0 – 5 = -5
∵ L.H.S. ≠ R.H.S
∴ p = 0 is not the solution
10 – 5 = 5
∵ L.H.S. = R.H.S
∴ p = 10 is a solution
5 – 5 = 0
∵ L.H.S. ≠ R.H.S
∴ p = 5 is not the solution
-5 -5 = -10
∵ L.H.S. ≠ R.H.S
∴ p = -5 is not the solution
![]()
(d) \(\frac{\mathrm{q}}{2}\) = 7
Putting the given values in L.H.S.,
\(\frac{\mathrm{7}}{2}\)
∵ L.H.S. ≠ R.H.S
∴ q = 7 is not the solution
\(\frac{\mathrm{2}}{2}\) = 1
∵ L.H.S. ≠ R.H.S
∴ q = 2 is not the solution
\(\frac{\mathrm{10}}{2}\) = 5
∵ L.H.S. ≠ R.H.S
∴ q = 10 is not the solution
\(\frac{\mathrm{14}}{2}\) = 7
∵ L.H.S. = R.H.S
∴ q = 14 is a solution
(e) r – 4 = 0
Putting the given values in L.H.S.,
4 – 4 = 0
∵ L.H.S. = R.H.S
∴ r = 4 is a solution
– 4 -4 = -8
∵ L.H.S. ≠ R.H.S
∴ r = – 4 is not the solution
8 – 4 = 4
∵ L.H.S. ≠ R.H.S
∴ r = 8 is not the solution
0 – 4 = – 4
∵ L.H.S. ≠ R.H.S
∴ r = 0 is not the solution
(f) x + 4 = 2
Putting the given values in L.H.S.,
-2 + 4 = 2
∵ L.H.S. = R.H.S
∴ x = -2 is a solution
0 + 4 = 4
∵ L.H.S. ≠ R.H.S
∴ x = 0 is not the solution
2 + 4 = 6
∵ L.H.S. ≠ R.H.S
∴ x = 0 is not the solution
4 + 4 = 8
∵ L.H.S. ≠ R.H.S
∴ x = 4 is not the solution
![]()
Question 4.
(a) Complete the table and by inspection of the table, find the solution to the equation m + 10 = 16.

(b) Complete the table and by inspection of the table, find the solution to the equation 5t = 35.

(c) Complete the table and find the solution of the equation z/3 = 4 using the table.

(d) Complete the table and find the solution to the equation m – 7 = 3

Answer:
(a)

∵ At m = 6, m + 10 = 16 ∴ m = 6 is the solution.
(b)

∵ At t = 7, 5t = 35 ∴ t = 7 is the solution.
(c)

∵ At z = 12, z/3 = 4 ∴ z = 12 is the solution.
(d)

∵ At m = 10, m- 7= 3 ∴ m = 10 is the solution.
![]()
Question 5.
Solve the following riddles, you may yourself construct such riddles.
Who am I?
(i) Go round a square
Counting every corner
Thrice and no more!
Add the count to me
To get exactly thirty four!
(ii) For each day of the week
Make an upcount from me
If you make no mistake
You will get twenty three!
(iii) I am a special number
Take away from me a six!
A whole cricket team
You will still be able to fix!
(iv) Tell me who I am
I shall give a pretty clue!
You will get me back
If you take me out of twenty two!
Answer:
(i) According to the condition,
1 + 12 = 34 or × + 12 = 34
∴ By inspection, we have
22 + 12 = 34
So, I am 22.
(ii) Let I am ‘×’.
We know that there are 7 days in a week.
∴ up-counting from × for 7, the sum = 23
By inspections, we have
16 + 7 = 23
∴ × = 16
Thus I am 16.
(iii) Let the special number be x and there are 11 players in cricket team.
∴ Special Number -6 = 11
× – 6 = 11
By inspection, we get
17 – 6 = 11
∴ × = 17
Thus I am 17.
(iv) Suppose I am ‘×’
∴ 22 – 1 = 1
or 22 – × = ×
By inspection, we have
22 -11 = 11
∴ × = 11
Thus I am 11.