These NCERT Solutions for Class 10 Maths Chapter Ex 4.2 Questions and Answers are prepared by our highly skilled subject experts.
NCERT Solutions for Class 10 Maths Chapter 4 Quadratic Equations Exercise 4.2
![]()
Question 1.
Find the roots of the following quadratic equations by factorisation:
(i) x2 – 3x – 10 = 0
(ii) 2x2 + x – 6 = 0
(iii) √2x2 + 7x + 5√2 = 0
(iv) 2x2 – x + \(\frac { 1 }{ 8 }\) = 0 8
(v) 100x2 – 20 x + 1 = 0
Solution:
(i) We have,
x² – 3x – 10 = 0
or x² – 5x + 2x – 10 = 0
or x(x – 5) – 2(x – 5) = 0
or, (x – 5) (x + 2) = 0
∴ x – 5 = 0 or, x + 2 = 0
⇒ x = 5 or, x + 2 = 0
Therefore, the roots x² – 2x -10 = 0 are – 5 and
(ii) We have,
2x² + x – 6 = 0
or, 2x² + 4x – 3x – 6 = 0
or, 2x(x + 2) – 3(x + 2) = 0
or, (x + 2) (2x – 3) = 0
∴ (x + 2) = 0 or, (2x – 3) = 0
⇒ x = – 2 or, x = \(\frac { 3 }{ 2 }\)
Therefore, the roots of 2x² + x – 6 = 0 are – 2 and \(\frac { 3 }{ 2 }\)
(iii) We have,
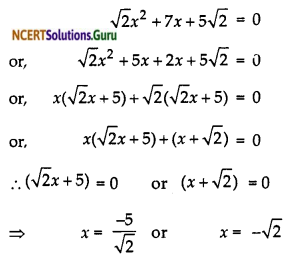
Therefore, the root of \(\sqrt{2}\)2x² + 7x + 5\(\sqrt{2}\) = o are \(\frac{-5}{\sqrt{2}}\) and \(\sqrt{2}\)
(iv) We have,

Therefore, the roots of 2x² – x + \(\frac { 1 }{ 8 }\) = 0 is \(\frac { 1 }{ 4 }\) ; \(\frac { 1 }{ 4 }\)
(v) We have,

Therefore, the roots of 100x² – 20x + 1 = 0 is \(\frac { 1 }{ 10 }\), \(\frac { 1 }{ 10 }\).
![]()
Question 2.
Solve the problems given in Example 1.
(i) John and Jivanti together have 45 marbles Both of them lost 5 marbles each, and the product of the number of marbles they now have is 124. We would like to find out how many marbles they had to start with.
(ii) A cottage industry produces a certain number of toys in a day. The cost of production of each toy in (in rupees) was found to be 55 minus the number of toys produced in a day. On a particular day, the total cost of production was ₹ 750. We would like to find out the number of toys produced on that day.
Solution:
(i) Let number of marbles John have be x
∴ Number of marbles Jivanti have = 45 – x
The number of marbles left with John when he lost 5 marbles = x – 5
The number of marbles left with Jivanti when she lost 5 marbles = 45x – x – 5 = 40 – x
According to question,
(x – 5) (40 – x) = 124
or 40x – x² – 200 + 5x = 124
or 45x – x² – 200 = 124
or x² – 45x + 324 = 0
or x² – 36x – 9x + 324 = 0
or x(x – 36) – 9(x – 36) = 0
or (x – 36) (x – 9) = 0
∴ (x – 36) =0 or (x – 9) = 0
⇒ x = 36 or x = 9
Therefore, if number of marbles John have be 36
Then number of marbles Jivanti have = 45 – x = 45 – 36 = 9
And, if number of marbles John have be 9
Then, number of marbles Jivanti have = 45 – x = 45 – 9 = 36
(ii) Let the number of toys produced on that day be x
Therefore; the cost of production (in rupees) of each toy that day = 55 – x
So, the total cost of production (in rupees) that day = x(55 – x)
According to question,
x(55 – x) = 750
or 55x – x² = 750
or x² – 55x + 750 = 0
or x² – 30x – 25x + 750 = 0
or x (x – 30) – 25 (x – 30) = 0
(x – 30) (x – 25) = 0
∴ (x – 30) = 0 or (x – 25) = 0
⇒ x = 30 or x = 25
Therefore, if the number of toys produced on that day is x = 30, then, the cost of production (in rupees) or each toy = 55 – x = 55 – 30 = ₹ 25.
And, if the number of toys produced is x = 25,
then, the cost of production = 55 – x = 55 – 25 = ₹ 30.
Question 3.
Find two numbers whose sum is 27, and product is 182.
Solution:
Let first number be x Second number be = 27 – x According to question,
x(27 – x) = 182 ‘
or 27x – x² = 182
or x² – 27x + 182 = 0
or x² – 14x – 13 + 182 = 0
or x (x – 14) – 13 (x – 14) = 0
or (x – 14) (x – 13) = 0
∴ (x – 14) = 0 or, (x – 13) = 0
⇒ x = 14 or x = 13
Therefore, if first number is 14 then second number is
27 – x = 27 – 14 = 13
And, if first number is 13 then second number is
27 – x = 27 – 13 = 14
![]()
Question 4.
Find two consecutive positive integers, sum of whose squares is 365.
Solution:
Let first consecutive positive integer be x
∴Second consecutive positive integer be x + 1
According to question,
x² + (x + 1)² = 365
or x² + x² + 2x + 1 = 365
or 2x² + 2x + 1 – 365 = 0
or 2x² + 2x – 364 = 0
or 2(x² + x – 182) = 0
or x² + x – 182 = 0
or x² + 14x – 13x – 182 = 0
or x(x + 14) – 13 (x + 14) = 0
or (x + 14) (x- 13) = 0
∴ (x + 14) = 0 or (x – 13) = 0
⇒ x = – 14 or x = 13
But, we has given that numbers are positive
∴ x = – 14 is neglected.
Therefore, x = 13
∴ First consecutive positive integer = x = 13
and second consecutive positive integer = 27 – x = 14
Question 5.
The altitude of a right traingle is 7 cm less than its base. If the hypotenuse is 13 cm, find the other two sides.
Solution:
Let the base of right angle triangle = x
∴ The height of right angle triangle = x – 7
And hypotenuse of right angle triangle = 13 cm
By Pythagoras theorem, we have,
(height)² + (base)² = (hypotenuse)²
∴ (x – 7)² + x² = (13)²
or x² – 14x + 49 + x² = 169
or 2x² – 14x + 49 – 169 = 0
or 2x² -14x – 120 = 0
or 2(x² – 7x – 60) = 0
or x² – 7x – 60 = 0
or x² – 12x + 5x – 60 = 0
or x (x – 12) + 5 (x – 12) = 0
or (x -12) (x + 5) = 0
∴ x – 12 = 0 or x + 5=0
⇒ x = 12 or x = – 5
But, length cannot be in negative
So, x = – 5 is neglected.
∴ x = 12
Therefore, base of the right angle triangle = x
∴ x = 12 cm
and height of the right angle triangle = x – 7 = 12 – 7 = 5 cm
![]()
Question 6.
A cottage industry produces a certain number of pottery articles in a day. It was observed on a particular day that the cost of production of each article (in rupees) was 3 more than twice the numbr of articles produced on that day. It the total cost of production on that was ₹ 90. Find the number of articles produced and the cost of each article.
Solution:
Let total number of articles produced = x
Cost of production = 2x + 3
According to question,
x (2x + 3) = 90
or 2x² + 3x = 90
or 2x² + 3x – 90 = 0
or 2x² + 15x – 12x – 90 = 0
or x(2x + 15) – 6 (2x + 15) = 0
or (2x +15) (x – 6) = 0
∴(2x + 15) = 0 or (x – 6) = 0
x = \(\frac { -15 }{ 2 }\) or x = 6
But, number of articles cannot be in negative.
So, x = \(\frac { -15 }{ 2 }\) is neglected.
∴ Total number of articles produced = x = 6
and cost of production = 2x + 3 = 2 x 6 + 3 = ₹ 15.