Do you need some help in preparing for your upcoming Maths exam? We’ve compiled a list of MCQ Questions for Class 12 Maths with Answers to get you started with the subject, Application of Integrals Class 12 MCQs Questions with Answers. You can download NCERT MCQ Questions for Class 12 Maths Chapter 8 Application of Integrals with Answers Pdf free download and learn how smart students improve problem-solving skills well ahead. So, ace up your preparation with Class 12 Maths Chapter 8 Application of Integrals Objective Questions.
Application of Integrals Class 12 MCQs Questions with Answers
Don’t forget to practice the multitude of MCQ Questions on Application of Integrals Class 12 with answers so you can apply your skills during the exam.
Question 1.
Area lying in the first quadrant and bounded by the circle x² + y² = 4 and the lines x = 0 and x = 2 is
(a) π
(b) \(\frac { π }{2}\)
(c) \(\frac { π }{3}\)
(d) \(\frac { π }{4}\)
Answer
Answer: (a) π
Question 2.
Area of the region bounded by the curve y² = 4x, y-axis and the line y = 3 is
(a) 2
(b) \(\frac { 9 }{4}\)
(c) \(\frac { 9 }{3}\)
(d) \(\frac { 9 }{2}\)
Answer
Answer: (a) 2
Question 3.
Smaller area enclosed by the circle x² + y² = 4 and the line x + y = 2 is
(a) 2 (π – 2)
(b) π – 2
(c) 2π – 1
(d) 2 (π + 2).
Answer
Answer: (b) π – 2
Question 4.
Area lying between the curves y² = 4x and y = 2 is:
(a) \(\frac { 2 }{3}\)
(b) \(\frac { 1 }{3}\)
(c) \(\frac { 1 }{4}\)
(d) \(\frac { 3 }{4}\)
Answer
Answer: (b) \(\frac { 1 }{3}\)
Question 5.
Area bounded by the curve y = x³, the x-axis and the ordinates x = -2 and x = 1 is
(a) -9
(b) –\(\frac { 15 }{4}\)
(c) \(\frac { 15 }{4}\)
(d) \(\frac { 17 }{4}\)
Answer
Answer: (b) –\(\frac { 15 }{4}\)
Question 6.
The area bounded by the curve y = x|x|, x-axis and the ordinates x = -1 and x = 1 is given by
(a) 0
(b) –\(\frac { 1 }{3}\)
(c) \(\frac { 2 }{3}\)
(d) \(\frac { 4 }{3}\)
Answer
Answer: (c) \(\frac { 2 }{3}\)
Question 7.
The area of the circle x² + y² = 16 exterior to the parabola y² = 6x is
(a) \(\frac { 4 }{3}\) (4π – √3)
(b) \(\frac { 1 }{3}\) (4π + √3)
(c) \(\frac { 2 }{3}\) (8π – √3)
(d) \(\frac { 4 }{3}\) (8π + √3)
Answer
Answer: (c) \(\frac { 2 }{3}\) (8π – √3)
Question 8.
The area enclosed by the circle x² + y² = 2 is equal to
(a) 4π sq. units
(b) 2√2 π sq. units
(c) 4π² sq. units
(d) 2π sq. units.
Answer
Answer: (d) 2π sq. units.
Question 9.
The area enclosed by the ellipse \(\frac { x^2 }{a^2}\) + \(\frac { y^2 }{b^2}\) = 1 is equal to
(a) π²ab
(b) πab
(c) πa²b
(d) πab².
Answer
Answer: (b) πab
Question 10.
The area of the region bounded by the curve y = x² and the line y = 16 is
(a) \(\frac { 32 }{3}\)
(b) \(\frac { 256 }{3}\)
(c) \(\frac { 64 }{3}\)
(d) \(\frac { 128 }{3}\)
Answer
Answer: (b) \(\frac { 256 }{3}\)
Question 11.
The area of the region bounded by the y-axis, y = cos x and y = sin x, 0 ≤ x ≤ \(\frac { π }{2}\) is
(a) √2 sq. units
(b) (√2 + 1) sq. units
(c) (√2 – 1) sq. units
(d) (2√2 – 1) sq. units.
Answer
Answer: (c) (√2 – 1) sq. units
Question 12.
The area of the region bounded by the curve x² = 4y and the straight line x = 4y – 2 is
(a) \(\frac { 3 }{8}\) sq. units
(b) \(\frac { 5 }{8}\) sq. units
(c) \(\frac { 7 }{8}\) sq. units
(d) \(\frac { 9 }{8}\) sq. units.
Answer
Answer: (d) \(\frac { 9 }{8}\) sq. units.
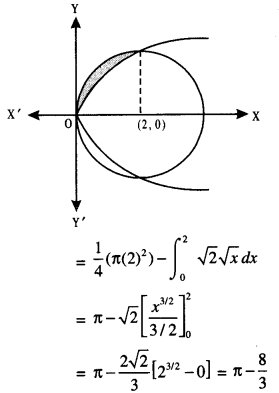
Question 13.
The area (in sq. units) of the region:
{(x, y) : y² ≥ 2x and x² + y2 ≤ 4x, x ≥ 0, y ≥ 0} is
(a) π – \(\frac { 8 }{3}\)
(b) π – \(\frac { 4√2 }{3}\)
(c) \(\frac { π }{2}\) – \(\frac { 2√2 }{3}\)
(d) π – \(\frac { 4 }{3}\)
Answer
Answer: (a) π – \(\frac { 8 }{3}\)
Hint:
y² = 2x is a parabola,
and x² + y² = 4x
⇒ (x – 2)² + y² = 4.
It is a circle having centre (2, 0) and radius 2 units.
∴ Reqd. area = Shaded region
Fill in the Blanks
Question 1.
The area of the quadrant of the circle x² + y² = 4 is …………….
Answer
Answer: π sq. units.
Question 2.
The area enclosed by the circle x² + y² = a² is ……………….
Answer
Answer: 2 π a² sq. units.
Question 3.
The area of the parabola y² = 4ax bounded by the latus-rectum is ………………
Answer
Answer: \(\frac { 8 }{3}\) a² sq. umts.
Question 4.
The area bounded by y = x², x = 0, x = 2 and x-axis is ……………….
Answer
Answer: \(\frac { 8 }{3}\) sq. units.
Question 5.
The area under the curve y = 2√x between x = 0 and x = 1 is ……………..
Answer
Answer: \(\frac { 4 }{3}\) sq. units.
We hope you found this NCERT MCQ Questions for Class 12 Maths Chapter 8 Application of Integrals with Answers Pdf free download helpful. If you have any questions about CBSE Class 12 Maths Application of Integrals MCQs Multiple Choice Questions with Answers, please share them in the comment box below and we will get back to you at the earliest possible time.