Do you need some help in preparing for your upcoming Maths exam? We’ve compiled a list of MCQ Questions for Class 12 Maths with Answers to get you started with the subject, Integrals Class 12 MCQs Questions with Answers. You can download NCERT MCQ Questions for Class 12 Maths Chapter 7 Integrals with Answers Pdf free download and learn how smart students improve problem-solving skills well ahead. So, ace up your preparation with Class 12 Maths Chapter 7 Integrals Objective Questions.
Integrals Class 12 MCQs Questions with Answers
Don’t forget to practice the multitude of MCQ Questions on Integrals Class 12 with answers so you can apply your skills during the exam.
Question 1.
The anti-derivative of (√x + \(\frac { 1 }{√x}\)) equals
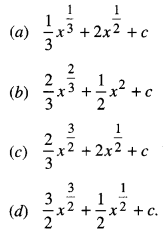
Answer
Answer: (c) \(\frac { 2 }{3}\) x\(\frac { 2 }{3}\) + 2x\(\frac { 1 }{2}\) + c
Question 2.
If \(\frac { 1 }{dx}\) (f(x)) = 4x³ – \(\frac { 3 }{x^4}\) such that f(2) = 0 then f(x) is ……………
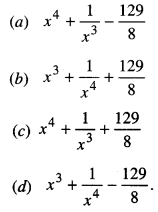
Answer
Answer: (a) x4 + \(\frac { 1 }{x^3}\) – \(\frac { 129 }{8}\)
Question 3.
∫\(\frac { 10x^9+10^x log_e 10 }{x^{10} + 10^x}\) dx equals
(a) 10x -x10 + c
(b) 10x + x10 + c
(c) (10x – x10)-1 + c
(d) log (10x + x10) + c.
Answer
Answer: (d) log (10x + x10) + c.
Question 4.
∫\(\frac { dx }{sin^2 x cos^2 x}\) equals
(a) tan x + cot x + c
(b) tan x – cot x + c
(c) tan x cot x + c
(d) tan x – cot 2x + c.
Answer
Answer: (b) tan x – cot x + c
Question 5.
∫\(\frac { sin^2 x – cos ^2 x }{sin^2 x cos^2 x}\) dx is equals to
(a) tan x + cot x + c
(b) tan x + cosec x + c
(c) -tan x + cot x + c
(d) tan x + sec x + c.
Answer
Answer: (a) tan x + cot x + c
Question 6.
∫\(\frac { e^x(1 + x) }{cos^2(xe^2)}\) dx is equals to
(a) -cot (xex) + c
(b) tan (xex) + c
(c) tan (ex) + c
(d) cot (ex) + c
Answer
Answer: (b) tan (xex) + c
Question 7.
∫\(\frac { dx }{x^2+2x+2}\) equals
(a) x tan-1 (x + 1) + c
(b) tan-1 (x + 1) + c
(c) (x + 1) tan-1 x + c
(d) tan-1 x + c.
Answer
Answer: (b) tan-1 (x + 1) + c
Question 8.
∫\(\frac { dx }{\sqrt{9-25x^2}}\) equals
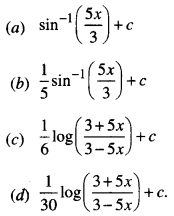
Answer
Answer: (b) \(\frac { 1 }{5}\) sin-1 (\(\frac { 5x }{3}\)) + c
Question 9.
∫\(\frac { x dx }{(x-1)(x-2)}\) equals
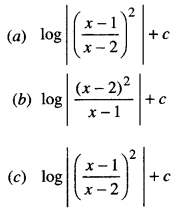
(d) log |(x – 1) (x – 2)| + c.
Answer
Answer: (b) log |\(\frac { (x-2)^2 }{x-1}\)| + c
Question 10.
∫\(\frac { dx }{x(x^2+1)}\) equals
(a) log |x| – \(\frac { 1 }{2}\) log (x² + 1) + c
(b) \(\frac { 1 }{2}\) log |x| + \(\frac { 1 }{2}\) log (x² + 1) + c
(c) -log |x| + \(\frac { 1 }{2}\) log (x² + 1) + c
(d) log |x| + log (x² + 1) + c
Answer
Answer: (a) log |x| – \(\frac { 1 }{2}\) log (x² + 1) + c
Question 11.
∫x² ex³ dx equals
(a) \(\frac { 1 }{3}\) ex³ + c
(b) \(\frac { 1 }{3}\) ex² + c
(c) \(\frac { 1 }{2}\) ex³ + c
(d) \(\frac { 1 }{2}\) ex² + c
Answer
Answer: (a) \(\frac { 1 }{3}\) ex³ + c
Question 12.
∫ex sec x (1 + tan x) dx equals
(a) ex cos x + c
(b) ex sec x + c
(c) ex sin x + c
(d) ex tan x + c.
Answer
Answer: (b) ex sec x + c
Question 13.
∫\(\sqrt { 1 + x^2}\) dx is equal to
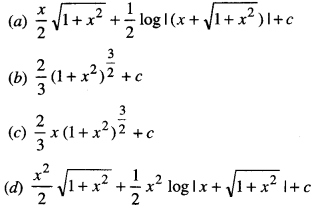
Answer
Answer:
![]()
Question 14.
∫\(\sqrt { x^2 – 8x + 7}\) dx is equal to
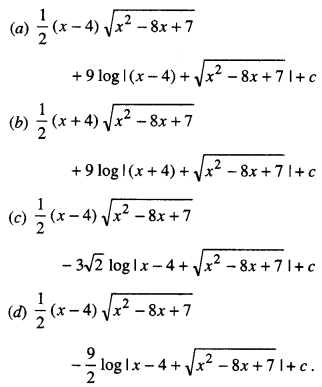
Answer
Answer:
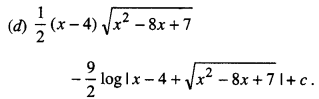
Question 15.
\(\int_{1}^{\sqrt{3}}\) \(\frac { dx }{1+x^2}\) equals
(a) \(\frac { π }{3}\)
(b) \(\frac { 2π }{3}\)
(c) \(\frac { π }{6}\)
(d) \(\frac { π }{112}\)
Answer
Answer: (d) \(\frac { π }{112}\)
Question 16.
\(\int_{1}^{2/3}\) \(\frac { dx }{4+9x^2}\) equals
(a) \(\frac { π }{6}\)
(b) \(\frac { π }{12}\)
(c) \(\frac { π }{24}\)
(d) \(\frac { π }{4}\)
Answer
Answer: (c) \(\frac { π }{24}\)
Question 17.
The value of the integral \(\int_{1}^{2/3}\) \(\frac { (x-x^3)^{1/3} }{x^4}\) dx is
(a) 6
(b) 0
(c) 3
(d) 4
Answer
Answer: (a) 6
Question 18.
If f(x) = \(\int_{0}^{x}\) t sin t dt, then f'(x) is
(a) cos x + x sin x
(b) x sin x
(c) x cos x
(d) sin x + x cos x.
Answer
Answer: (b) x sin x
Question 19.
The value of
\(\int_{-π/2}^{π/2}\) (x³ + x cos x + tan5 x + 1) dx is
(a) 0
(b) 2
(c) π
(d) 1
Answer
Answer: (c) π
Question 20.
The value of \(\int_{0}^{π/2}\) log (\(\frac { 4+3 sin x }{4+3 cos x}\)) dx is
(a) 2
(b) \(\frac { 3 }{4}\)
(c) 0
(d) -2
Answer
Answer: (c) 0
Question 21.
∫\(\frac { dx }{e^x+e{-x}}\) is equal to
(a) tan-1 (ex) + c
(b) tan-1 (e-x) + c
(c) log (ex – e-1) + c
(d) log (ex + e-x) + c.
Answer
Answer: (a) tan-1 (ex) + c
Question 22.
∫\(\frac { cos 2x }{(sin x + cos x)^2}\) dx is equal to
(a) \(\frac { -1 }{sin x + cos x}\) + c
(b) log |sin x + cos x| + c
(c) log |sin x – cos x| + c
(d) \(\frac { 1 }{(sin x + cos x)^2}\) + c
Answer
Answer: (b) log |sin x + cos x| + c
Question 23.
If f (a + b – x) = f(x), then \(\int_{a}^{b}\) x f(x) dx is equal to
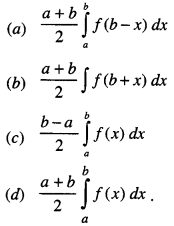
Answer
Answer: (d) \(\frac { a+b }{2}\) \(\int_{a}^{b}\) f(x) dx
Question 24.
∫ex(cos x – sin x)dx is equal to
(a) ex – cos x + c
(b) ex sin x + c
(c) -ex cos x + c
(d) -ex sin x + c.
Answer
Answer: (a) ex – cos x + c
Question 25.
∫\(\frac { dx }{sin^2 x cos^2 x}\) is equal to
(a) tan x + cot x + c
(b) (tan x + cot x)² + c
(c) tan x – cot x + c
(d) (tan x – cot x)² + c.
Answer
Answer: (c) tan x – cot x + c
Question 26.
If ∫ \(\frac { 3e^x-5e^{-x} }{4r^x+5e^{-x}}\) dx = ax + b log |4ex + 5e-x| + c then
(a) a = –\(\frac { 1 }{8}\), b = \(\frac { 7 }{8}\)
(b) a = \(\frac { 1 }{8}\), b = \(\frac { 7 }{8}\)
(c) a = \(\frac { -1 }{8}\), b = –\(\frac { 7 }{8}\)
(d) a = \(\frac { 1 }{8}\), b = –\(\frac { 7 }{8\)
Answer
Answer: (a) a = –\(\frac { 1 }{8}\), b = \(\frac { 7 }{8}\)
Question 27.
∫tan-1 √x dx is equal to
(a) (x + 1)tan-1 √x – √x + c
(b) x tan-1 √x – √x + c
(c) √x – x tan-1 √x + c
(d) -1x – (x + 1) tan-1 √x + c
Answer
Answer: (a) (x + 1)tan-1 √x – √x + c
Question 28.
∫ex(\(\frac { 1-x }{(1+x^2)}\))2 dx is equal to:
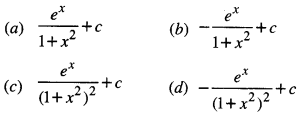
Answer
Answer: (c) \(\frac { e^x }{(1+x^2)^2}\) + c
Question 29.
\(\int_{a+c}^{b+c}\) f(x)dx is equal to :
(a) \(\int_{c}^{b}\) f(x – c)dx
(b) \(\int_{c}^{b}\) f(x + c)dx
(c) \(\int_{c}^{b}\) f(x)dx
(d) \(\int_{a-c}^{b-c}\)
Answer
Answer: (b) \(\int_{c}^{b}\) f(x + c)dx
Question 30.
\(\int_{-1}^{1}\) \(\frac { x^3+|x|+1 }{x^2+2|x|+1}\) is equal to
(a) log 2
(b) 2 log 2
(c) \(\frac { 1 }{2}\) log 2
(d) 4 log 2
Answer
Answer: (b) 2 log 2
Question 31.
\(\int_{c}^{b}\) |x cos πx|dx is equal to
(a) \(\frac { 8 }{π}\)
(b) \(\frac { 4 }{π}\)
(c) \(\frac { 2 }{π}\)
(d) \(\frac { 1 }{π}\)
Answer
Answer: (a) \(\frac { 8 }{π}\)
Question 32.
If \(\int_{0}^{1}\) \(\frac { e^t }{1+t}\) dt = a, then \(\int_{0}^{1}\) \(\frac { e^t }{(1+t)^2}\)
(a) a – 1 + \(\frac { e }{2}\)
(b) a + 1 – \(\frac { e }{2}\)
(c) a – 1 – \(\frac { e }{2}\)
(d) a + 1 + \(\frac { e }{2}\)
Answer
Answer: (b) a + 1 – \(\frac { e }{2}\)
Question 33.
If x = \(\int_{0}^{y}\) \(\frac { dt }{\sqrt{1+9t^2}}\) and \(\frac { d^y }{dx^2}\) = ay, then a is equal to
(a) 3
(b) 6
(c) 9
(d) 1.
Answer
Answer: (c) 9
Question 34.
Let I = \(\int_{0}^{1}\) \(\frac { sin x }{√x}\) dx and J = \(\int_{0}^{1}\) \(\frac { cos x }{√x}\) dx. Then which of the following is true?
(a) I > \(\frac { 2 }{3}\) and J < 2
(b) I > \(\frac { 2 }{3}\) and J > 2
(c) I < \(\frac { 2 }{3}\) and J < 2
(d) I < \(\frac { 2 }{3}\) and J > 2.
Answer
Answer: (c) I < \(\frac { 2 }{3}\) and J < 2
Hint:
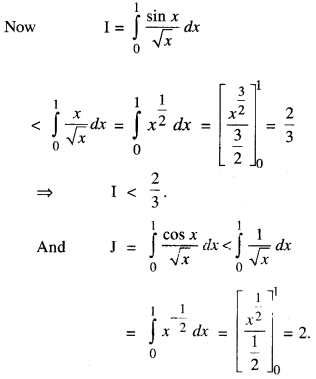
Question 35.
\(\int_{0}^{π}\) [cot x]dx, where [ . ] denotes the greatest integer function, is equal to
(a) \(\frac { π }{2}\)
(b) 2
(c) -1
(d) –\(\frac { π }{2}\)
Answer
Answer: (d) –\(\frac { π }{2}\)
Hint:
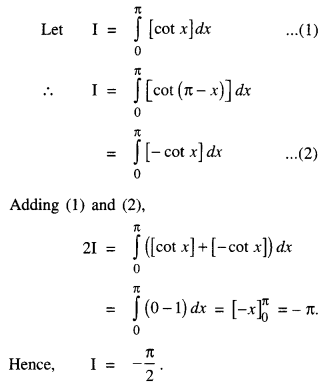
Question 36.
Let p (x) be a function defined on R such that p'(x) = p'(1 – x), for all x ∈ [0, 1], p(0) = 1 and p (1) = 41.
Then \(\int_{0}^{1}\) p(x) dx equals
(a) \(\sqrt { 41}\)
(b) 21
(c) 41
(d) 42
Answer
Answer: (b) 21
Hint:
Here p'(x) – p'(1 – x).
Integrating, p (x) = -p (1 – x) + c ………… (1)
At x = 0, p(0) = -p (1) + c
⇒ 1 = -41 + c ⇒ c = 42.
Putting in (1),
p (x) = -p(1 – x) + 42
∴ \(\int_{0}^{1}\) p(x) dx = –\(\int_{0}^{1}\) p(1 – x)dx + \(\int_{0}^{1}\) 42 dx
⇒ 21 = 42[x]\(_{ 0 }^{1}\)
⇒ 21 = 42
⇒ I = 21.
Question 37.
Let In = ∫tan” x dx, (n > 1).
If I4 + I6 = a tan5 x + bx5 + c, where c is a constant of integration, then the ordered pair (a, b) is equal to
(a) (\(\frac { 1}{5}\), -1)
(b) (-\(\frac { 1}{5}\), 0)
(c) (-\(\frac { 1}{5}\), 1)
(d) (\(\frac { 1}{5}\), 0)
Answer
Answer: (d) (\(\frac { 1}{5}\), 0)
Hint:
Here I4 + I6 = a tan5 x + bx5 + c
⇒ ∫tan4x dx + ∫tan6 x dx = a tan5 x + bx5 + c.
Diff. both sides,
tan4 x + tan6 x = 5a tan4 x sec² x + 5bx4
= 5 a tan4 x(1 + tan2 x) + 5 bx4
= 5a tan4 x + 5a tan6x + 5bx4.
Comparing, 1 = 5a and 5b = 0
⇒ a = \(\frac { 1 }{5}\) and b = 0.
Hence, (a, b) = (\(\frac { 1}{5}\), 0)
Question 38.
The integral
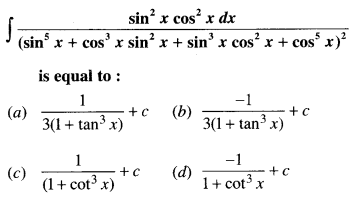
Answer
Answer: (b) \(\frac {-1}{3(1+tan^3 x)}\) + c
Hint:
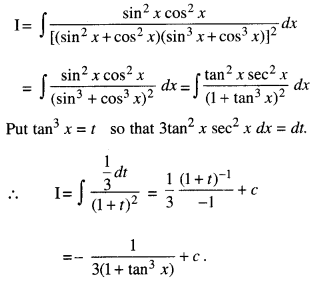
Question 39.
The value of \(\int_{-π/2}^{π/2}\) \(\frac { sin^2 x }{1 + 2^x}\) dx is
(a) \(\frac { π}{8}\)
(b) \(\frac {π}{2}\)
(c) 4π
(d) \(\frac {π}{4}\)
Answer
Answer: (d) \(\frac {π}{4}\)
Hint:
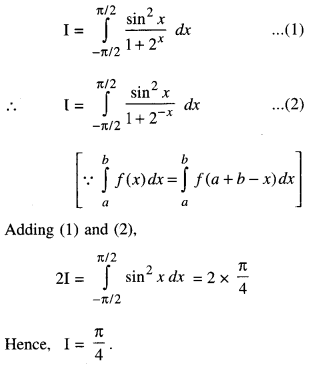
Fill in the blanks
Question 1.
∫(√x + \(\frac {1}{√x}\)) dx (x ≠ 0) = ………………
Answer
Answer: \(\frac { 2 }{3}\) x√x + 2√x
Question 2.
∫cot x dx = ………………….
Answer
Answer: log |sin x| + c
Question 3.
∫sec x dx = ………………
Answer
Answer: log |sec x + tan x| + c
Question 4.
∫ \(\frac { sin^2 x – cos^2 x }{sin x cos x}\) dx = ………………..
Answer
Answer: log |sec x| – log |sin x| + c
Question 5.
∫ \(\frac { x^3+5x^2+4 }{x^2}\) dx = ………………
Answer
Answer: \(\frac { x^2 }{2}\) + 5x – \(\frac { 4 }{x}\) + c
Question 6.
∫tan² x dx ………………..
Answer
Answer: tan x – x+ c
Question 7.
∫ \(\sqrt { a^2+x^2}\) dx = ………………..
Answer
Answer: \(\frac{x \sqrt{a^{2}+x^{2}}}{2}\) + \(\frac { a^2 }{2}\) log|x + \(\sqrt { a^2+x^2}\)| + c
Question 8.
∫ (2 – x) sin x dx = ……………..
Answer
Answer: -2 cos x + x cos x – sin x + c
Question 9.
If ∫ ex(tan x + 1) sec x dx = ex f(x) + c, then f(x) = ………………
Answer
Answer: sec x
Question 10.
∫ \(\frac { 1 }{9x^2-1}\) dx = …………….
Answer
Answer: \(\frac { 1 }{6}\) log |\(\frac { 3x-1 }{3x+1}\)| + c
Question 11.
\(\int_{2}^{3}\) 3x dx = …………………….
Answer
Answer: \(\frac { 18 }{log 3}\)
Question 12.
\(\int_{0}^{1}\) \(\frac { dx }{\sqrt{1+x^2}}\) = ……………..
Answer
Answer: log (1 + √2)
Question 13.
If \(\int_{0}^{1}\) (3x² + 2x + k) dx = 0, then the value of ‘k’ ………………..
Answer
Answer: -2
Question 14.
If f(x) = \(\int_{0}^{x}\) t sin t dt, then the value of f'(x) = ………………….
Answer
Answer: x sin x
Question 15.
\(\int_{0}^{1.5}\) [x] dx = ………………. where [x] is greatest integer function.
Answer
Answer: 0.5
We hope you found this NCERT MCQ Questions for Class 12 Maths Chapter 7 Integrals with Answers Pdf free download helpful. If you have any questions about CBSE Class 12 Maths Integrals MCQs Multiple Choice Questions with Answers, please share them in the comment box below and we will get back to you at the earliest possible time.