Do you need some help in preparing for your upcoming Maths exam? We’ve compiled a list of MCQ Questions for Class 12 Maths with Answers to get you started with the subject, Application of Derivatives Class 12 MCQs Questions with Answers. You can download NCERT MCQ Questions for Class 12 Maths Chapter 6 Application of Derivatives with Answers Pdf free download and learn how smart students improve problem-solving skills well ahead. So, ace up your preparation with Class 12 Maths Chapter 6 Application of Derivatives Objective Questions.
Application of Derivatives Class 12 MCQs Questions with Answers
Don’t forget to practice the multitude of MCQ questions on Application of Derivatives Class 12 with answers so you can apply your skills during the exam.
Question 1.
The rate of change of the area of a circle with respect to its radius r at r = 6 cm is:
(a) 10π
(b) 12π
(c) 8π
(d) 11π
Answer
Answer: (b) 12π
Question 2.
The total revenue received from the sale of x units of a product is given by R (x) = 3x² + 36x + 5. The marginal revenue, when x = 15 is:
(a) 116
(b) 96
(c) 90
(d) 126.
Answer
Answer: (d) 126.
Question 3.
The interval in which y = x² e-x is increasing with respect to x is:
(a) (-∞, ∞)
(b) (-2,0)
(c) (2, ∞)
(d) (0, 2).
Answer
Answer: (d) (0, 2).
Question 4.
The slope of the normal to the curve y = 2x² + 3 sin x at x = 0 is
(a) 3
(b) \(\frac { 1 }{3}\)
(c) -3
(d) –\(\frac { 1 }{3}\)
Answer
Answer: (d) –\(\frac { 1 }{3}\)
Question 5.
The line y = x + 1 is a tangent to the curve y² = 4x at the point:
(a) (1, 2)
(b) (2, 1)
(c) (1, -2)
(d) (-1, 2).
Answer
Answer: (a) (1, 2)
Question 6.
If f(x) = 3x² + 15x + 5, then the approximate value of f(3.02) is:
(a) 47.66
(b) 57.66
(c) 67.66
(d) 77.66.
Answer
Answer: (d) 77.66.
Question 7.
The approximate change in the volume of a cube of side x metres caused by increasing the side by 3% is:
(a) 0.06 x³ m³
(b) 0.6 x³ m³
(c) 0.09 x³m³
(d) 0.9 x³ m³
Answer
Answer: (c) 0.09 x³m³
Question 8.
The point on the curve x² = 2y, which is nearest to the point (0, 5), is:
(a) (2 √2, 4)
(b) (2 √2, 0)
(c) (0, 0)
(d) (2, 2).
Answer
Answer: (a) (2 √2, 4)
Question 9.
For all real values of x, the minimum value of \(\frac { 1-x+x^2 }{1+x+x^2}\) is
(a) 0
(b) 1
(c) 3
(d) \(\frac { 1 }{3}\)
Answer
Answer: (d) \(\frac { 1 }{3}\)
Question 10.
The maximum value of [x (x – 1) + 1]1/3, 0 ≤ x ≤ 1 is
(a) (\(\frac { 1 }{3}\))\(\frac { 1 }{3}\)
(b) \(\frac { 1 }{2}\)
(c) 1
(d) 0
Answer
Answer: (c) 1
Question 11.
A cylindrical tank of radius 10 mis being filled with wheat at the rate of 314 cubic m per minute. Then the depth of the wheat is increasing at the rate of:
(a) 1 m/minute
(b) 0 × 1 m/minute
(c) 1 × 1 m/minute
(d) 0 × 5 m/minute.
Answer
Answer: (a) 1 m/minute
Question 12.
The slope of the tangent to the curve x = t² + 3t – 8, y = 2 t² – 2t – 5 at the point (2, -1) is:
(a) \(\frac { 22 }{7}\)
(b) \(\frac { 6 }{7}\)
(c) \(\frac { 7 }{6}\)
(d) \(\frac { -6 }{7}\)
Answer
Answer: (b) \(\frac { 6 }{7}\)
Question 13.
The line y = mx + 1 is a tangent to the curve y² = 4x if the value of m is:
(a) 1
(b) 2
(c) 3
(d) \(\frac { 1 }{2}\)
Answer
Answer: (a) 1
Question 14.
The normal at the point (1, 1) on the curve 2y + x² = 3 is
(a) x + y = 0
(b) x – y = 0
(c) x + y + 1 = 0
(d) x – y + 1 = 0.
Answer
Answer: (b) x – y = 0
Question 15.
The normal to the curve x² = 4y passing through (2, 1) is:
(a) x + y = 3
(b) x – y = 3
(c) x + y = 1
(d) x – y = 1.
Answer
Answer: (a) x + y = 3
Question 16.
The points on the curve 9y² = x³, where the normal to the curve makes equal intercepts with the axes are
(a) (4, ±\(\frac { 8 }{3}\))
(b) (4, –\(\frac { 8 }{3}\))
(c) (4, ±\(\frac { 3 }{8}\))
(d) (±4, \(\frac { 3 }{8}\))
Answer
Answer: (a) (4, ±\(\frac { 8 }{3}\))
Question 17.
The abscissa of the point on the curve 3y = 6x – 5x³, the normal at which passes through origin is:
(a) 1
(b) \(\frac { 1 }{3}\)
(c) 2
(d) \(\frac { 1 }{2}\)
Answer
Answer: (a) 1
Question 18.
The two curves x³ – 3xy² + 2 = 0 and 3x²y – y³ = 2
(a) touch each other
(b) cut at right angle
(c) cut at an angle \(\frac { π }{3}\)
(d) cut at an angle \(\frac { π }{4}\)
Answer
Answer: (b) cut at right angle
Question 19.
The tangent to the curve given by:
x = et cos t, y = et sm t at t = \(\frac { π }{4}\) makes with x-axis an angle:
(a) 0
(b) \(\frac { π }{4}\)
(c) \(\frac { π }{3}\)
(d) \(\frac { π }{2}\)
Answer
Answer: (d) \(\frac { π }{2}\)
Question 20.
The equation of the normal to the curve y = sin x at (0, 0) is
(a) x = 0
(b) y = 0
(c) x + y = 0
(d) x – y = 0.
Answer
Answer: (c) x + y = 0
Question 21.
The point on the curve y² = x, where the tangent makes an angle of \(\frac { π }{4}\) with x-axis is:
(a) (\(\frac { 1 }{2}\), \(\frac { 1 }{4}\))
(b) (\(\frac { 1 }{4}\), \(\frac { 1 }{2}\))
(c) (4, 2)
(d) (1, 1).
Answer
Answer: (b) (\(\frac { 1 }{4}\), \(\frac { 1 }{2}\))
Question 22.
Let f: R → R be a positive increasing function with:
\( \lim _{x \rightarrow \infty}\) \(\frac { f(3x) }{f(x)}\) = 1. Then \( \lim _{x \rightarrow \infty}\) \(\frac { f(2x) }{f(x)}\) =
(a) 1
(b) \(\frac { 2 }{3}\)
(c) \(\frac { 3 }{2}\)
(d) 3.
Answer
Answer: (a) 1
Hint:
Since f(x) is a positive increasing function
∴ 0 < f(x) < f(2x) < f(3x)

Question 23.
The real number k for which the equation 2x³ + 3x + k = 0 has two distinct real roots in [0,1]:
(a) lies between 2 and 3
(b) lies between -1 and 0
(c) does not exist
(d) lies between 1 and 2.
Answer
Answer: (c) does not exist
Hint:
If 2x³ + 3x + k = 0 has two distinct real roots in [0, 1], then f'(x) will change sign.
But f'(x) = cx² + 3 > 0
Hence, no value of k exists.
Question 24.
If f and g are differentiable functions on [0, 1] satisfying f(0) = 2 = g(l), g(0) = 0 and f(1) = 6, then for some c ∈ ] 0, 1 [:
(a) 2f'(c) = 3g'(c)
(b) f'(c) = g'(c)
(c) f'(c) = 2g'(c)
(d) 2f'(c) = g'(c).
Answer
Answer: (c) f'(c) = 2g'(c)
Hint:
Let h(x) = f(x) – 2g(x).
∴ h'(x) =f'(x) – 2g'(x).
Here h(0) = h(1) = 2.
By Rolle’s Theorem, h’ (c) = 0
⇒ f'(c) = 2g'(c).
Question 25.
Twenty metres of wire is available for fencing off a flower-bed in the form of a circular sector. Then the maximum area (in sq. m) of the flower bed is:
(a) 25
(b) 30
(c) 12.5
(d) 10.
Answer
Answer: (a) 25
Hint:
Total length = r + r + rθ = 20
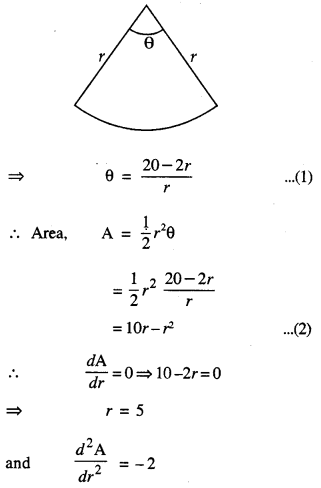
∴ r = 5 gives max-area.
Hence, from (2) maximum area,
A =10(5) – 25 = 25.
Question 26.
Let f (x) = x² – \(\frac { 1 }{x^2}\) and g(x) = x – \(\frac { 1 }{x}\), x ∈ R – {-1, 0, 1}. If h(x) = \(\frac { f(x) }{g(x)}\), then the local minimum value of h(x) is:
(a) 3
(b) -3
(c) -2√2
(d) 2√2.
Answer
Answer: (d) 2√2.
Hint:
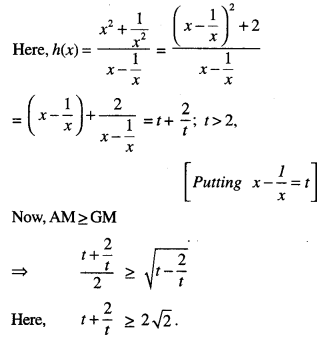
Fill in the blanks
Question 1.
Rate of change of the area of a circle with respect to its radius when r = 4 cm is ……………..
Answer
Answer: 8π cm²/m.
Question 2.
Rate of change of the volume of a ball with respect to its radius is ………………
Answer
Answer: 4πr²
Question 3.
The function f(x) = |x| is strictly ……………… in (0, ∞)
Answer
Answer: Increasing.
Question 4.
Logarithmic function is strictly ………………. in (0, ∞).
Answer
Answer: Increasing.
Question 5.
The value of ‘a’ for which f(x) = sin x – ax + b is decreasing function on R is ……………..
Answer
Answer: ≤ 1.
Question 6.
Slope of the tangent to the curve x = at², y = 2t at t = 2 is ……………..
Answer
Answer: \(\frac { 1 }{2}\)
Question 7.
If tangent to the curve y² + 3x – 7 = 0 at the point (h, k) is parallel to like x – y – 4, then the value of k is ……………….
Answer
Answer: –\(\frac { 3 }{2}\)
Question 8.
For the curve y = 5x – 2x³, if x increases at the tangents of 2 units/sec; then at x = 3 the slope of the curve is changes at ……………..
Answer
Answer: decreasing at the rate of 72 units/sec.
Question 9.
If x > 0, y > 0 and xy = 5, then the minimum value of x + y is ………………
Answer
Answer: 10.
Question 10.
Maximum value of:
f(x) = – (x – 1)² + 2 is ………………
Answer
Answer: 2.
We hope you found this NCERT MCQ Questions for Class 12 Maths Chapter 6 Application of Derivatives with Answers Pdf free download helpful. If you have any questions about CBSE Class 12 Maths Application of Derivatives MCQs Multiple Choice Questions with Answers, please share them in the comment box below and we will get back to you at the earliest possible time.