Do you need some help in preparing for your upcoming Maths exam? We’ve compiled a list of MCQ Questions for Class 12 Maths with Answers to get you started with the subject, Three Dimensional Geometry Class 12 MCQs Questions with Answers. You can download NCERT MCQ Questions for Class 12 Maths Chapter 11 Three Dimensional Geometry with Answers Pdf free download and learn how smart students improve problem-solving skills well ahead. So, ace up your preparation with Class 12 Maths Chapter 11 Three Dimensional Geometry Objective Questions.
Three Dimensional Geometry Class 12 MCQs Questions with Answers
Don’t forget to practice the multitude of MCQ Questions on Three Dimensional Geometry Class 12 with answersso you can apply your skills during the exam.
Question 1.
Distance between two planes:
2x + 3y + 4z = 5 and 4x + 6y + 8z = 12 is
(a) 2 units
(b) 4 units
(c) 8 units
(d) \(\frac { 1 }{\sqrt{29}}\) units.
Answer
Answer: (d) \(\frac { 1 }{\sqrt{29}}\) units.
Question 2.
The planes 2x – y + 4z = 3 and 5x – 2.5y +10 z = 6 are
(a) perpendicular
(b) parallel
(c) intersect along y-axis
(d) passes through (0, 0, \(\frac { 5 }{4}\))
Answer
Answer: (b) parallel
Question 3.
The co-ordinates of the foot of the perpendicular drawn from the point (2, 5, 7) on the x-axis are given by:
(a) (2, 0, 0)
(b) (0, 5, 0)
(c) (0, 0, 7)
(d) (0, 5, 7).
Answer
Answer: (a) (2, 0, 0)
Question 4.
If α, ß, γ are the angles that a line makes with the positive direction of x, y, z axis, respectively, then the direction-cosines of the line are:
(a) < sin α, sin ß, sin γ >
(b) < cos α, cos ß, cos γ >
(c) < tan α, tan ß, tan γ >
(d) < cos² α, cos² ß, cos² γ >.
Answer
Answer: (b) < cos α, cos ß, cos γ >
Question 5.
The distance of a point P(a, b, c) from x-axis is
(a) \(\sqrt { a^2+c^2}\)
(b) \(\sqrt { a^2+b^2}\)
(c) \(\sqrt { b^2+c^2}\)
(d) b² + c².
Answer
Answer: (c) \(\sqrt { b^2+c^2}\)
Question 6.
If the direction-cosines of a line are < k, k, k >, then
(a) k > 0
(b) 0 < k < 1
(c) k = 1
(d) k = \(\frac { 1 }{√3}\) or –\(\frac { 1 }{√3}\)
Answer
Answer: (c) k = 1
Question 7.
The reflection of the point (α, ß, γ) in the xy-plane is:
(a) (α, ß, 0)
(b) (0, 0, γ)
(c) (-α, -ß, γ)
(d) (α, ß, -γ).
Answer
Answer: (d) (α, ß, -γ).
Question 8.
What is the distance (in units) between two planes:
3x + 5y + 7z = 3 and 9x + 15y + 21z = 9?
(a) 0
(b) 3
(c) \(\frac { 6 }{\sqrt{83}}\)
(d) 6.
Answer
Answer: (a) 0
Hint:
The given planes are
3x + 5y + 7z = 3 ……(1)
and 9x + 15y + 21z = 9 …….(2)
Dividing (2) by 3, 3x + 5y + 7z = 3, which is (1)
Thus, the given planes are coincident and as such the distance between them = 0 (units).
Question 9.
The equation of the line in vector form passing through the point (-1, 3, 5) and parallel to line \(\frac { x-3 }{2}\) = \(\frac { y-4 }{3}\), z = 2 is
(a) \(\vec r\) = (-\(\hat i\) + 3\(\hat j\) + 5\(\hat k\)) + λ(2\(\hat i\) +3\(\hat j\) + \(\hat k\))
(b) \(\vec r\) = (-\(\hat i\)+ 3\(\hat j\) + 5\(\hat k\)) + λ(2\(\hat i\) + 3\(\hat j\))
(c) \(\vec r\) = (2\(\hat i\)+ 3\(\hat j\) – 2\(\hat k\)) + λ(-\(\hat i\) + 3\(\hat j\) + 5\(\hat k\))
(d) \(\vec r\) = (2\(\hat i\) + 3\(\hat j\)]) + λ(-\(\hat i\) + 3\(\hat j\) + 5\(\hat k\)).
Answer
Answer: (b) \(\vec r\) = (-\(\hat i\)+ 3\(\hat j\) + 5\(\hat k\)) + λ(2\(\hat i\) + 3\(\hat j\))
Hint:
The given line is
\(\frac { x-3 }{2}\) = \(\frac { y-4 }{3}\) = \(\frac { z-2 }{0}\)
∴ Reqd. equation of the line is:
\(\vec r\) = (-\(\hat i\)+ 3\(\hat j\) + 5\(\hat k\)) + λ(2\(\hat i\) + 3\(\hat j\))
Question 10.
Let the line \(\frac { x-2 }{3}\) = \(\frac { y-1 }{-5}\) = \(\frac { z-2 }{2}\) lie in the plane x + 3y – αz + ß = 0. Then (α, ß) equals:
(a) (-6, -17)
(b) (5, -15)
(c) (-5, 5)
(d) (6, -17).
Answer
Answer: (a) (-6, -17)
Hint:
The line = \(\frac { x-2 }{3}\) = \(\frac { y-1 }{-5}\) = \(\frac { z-2 }{2}\) lies in the plane x + 3y – αz + ß = 0,
∴ 2 + 3(1) – α(2) + ß = 0
⇒ 2α – ß = 5
and (1)(3) + (-5)(3) + (2) (-α) = 0
⇒ 3 – 15 – 2α = 0
⇒ 2α = -12α
⇒ α = -6.
Putting in (1),
2(-6) – ß = 5
⇒ ß = -12 – 5 = -17.
Hence, (α, ß) is (-6, -17).
Question 11.
The projections of a vector on the three co-ordinate axes are 6, -3, 2 respectively. The direction-cosines of the vector are:
(a) \(\frac { 6 }{5}\), –\(\frac { 3 }{5}\), \(\frac { 2 }{5}\)
(b) \(\frac { 6 }{7}\), –\(\frac { 3}{7}\), \(\frac { 2 }{7}\)
(c) \(\frac { -6 }{7}\), \(\frac { -3 }{7}\), \(\frac { 1 }{7}\)
(d) 6, -3, 2.
Answer
Answer: (b) \(\frac { 6 }{7}\), –\(\frac { 3}{7}\), \(\frac { 2 }{7}\)
Hint:
Direction-cosines are:
< \(\frac { 6 }{\sqrt{36+9+4}}\), \(\frac {-3}{\sqrt{36+9+4}}\), \(\frac { 2 }{\sqrt{36+9+4}}\) >
i.e., < \(\frac { 6 }{7}\), –\(\frac { 3}{7}\), \(\frac { 2 }{7}\) >.
Question 12.
A line AB in three-dimensional space makes angles 45° and 120° with the positive x-axis and the positive y-axis respectively. If AB makes an acute angle θ with the positive z-axis, then θ equals:
(a) 30°
(b) 45°
(c) 60°
(d) 15°.
Answer
Answer: (c) 60°
Hint:
cos² α + cos² ß + cos² γ = 1
Here α = 45°, ß = 120°, γ = 0.
∴ cos² 45° + cos² 120° + cos² θ = 1
⇒ \(\frac { 1 }{2}\) + \(\frac { 1 }{4}\) + cos² θ = 1
⇒ 1 – cos² θ = \(\frac { 3 }{4}\)
⇒sin² θ = \(\frac { 3 }{4}\) = sin² 60°
⇒ θ = 60°
Question 13.
If the angle between the line x = \(\frac { y-1 }{2}\) = \(\frac { z-3 }{λ}\) and the plane x + 2y + 3z = 4is cos-1 (\(\sqrt{\frac { 5}{14}}\)) then λ, equals:
(a) \(\frac { 2 }{3}\)
(b) \(\frac { 3 }{2}\)
(c) \(\frac { 2 }{5}\)
(d) \(\frac { 5 }{3}\)
Answer
Answer: (a) \(\frac { 2 }{3}\)
Hint:
The given line is \(\frac { x-0 }{1}[/latex = [latex]\frac { y-1 }{2}\) = \(\frac { z-3 }{λ}\) and the plane is x + 2y + 3z = 4.
∴ Angle between the line and the plane is:
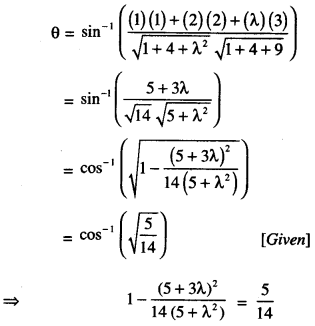
⇒ 14 (5 + λ²) – (25 + 9λ² + 30λ) = 5(5 + λ²)
⇒ 45 + 5λ² – 30λ = 25 + 5λ²
⇒ 30λ = 20
⇒ λ = \(\frac { 2 }{3}\)
Question 14.
The length of the perpendicular drawn from the point (3, -1, 11) to the line \(\frac { x }{2}\) = \(\frac { y-2 }{3}\) = \(\frac { z-3 }{4}\) is
(a) \(\sqrt { 29}\)
(b) \(\sqrt { 33}\)
(c) \(\sqrt { 53}\)
(d) \(\sqrt { 65}\)
Answer
Answer: (c) \(\sqrt { 53}\)
Hint:
Let any point on the line
\(\frac { x }{2}\) = \(\frac { y-2 }{3}\) = \(\frac { z-3 }{4}\) be P (2k, 2 + 3k, 3 + 4k).
If P be the foot of perpendicular,then direction ratios of the perpendicular are
< 2k – 3, 2 + 3k + 1, 3 + 4k – 11 >
i.e.< 2k -3, 3k + 3, 4k – 8 >.
And direction-ratios of the line are < 2, 3, 4 >.
∴ 2 (2k – 3) + 3 (3k + 3) + 4(4k – 8) = 0
⇒ 29k – 29 = 0
⇒ k = 1.
∴ P is (2, 2 + 3, 3 + 4) i.e. (2, 5, 7).
Also Q is (3, -1, 11).
∴ Length of perpendicular
= \(\sqrt {(2 – 3)^2 + (5 + 1)^2 + (7 – 11)^2}\)
= \(\sqrt {1 + 36 + 16}\)
= \(\sqrt {53}\)
Question 15.
The distance of the point (1, -5, 9) from the plane x – y + z = 5, measured along a straight line x = y = z is:
(a) 10√3
(b) 5√3
(c) 3\(\sqrt {10}\)
(d) 3√5
Answer
Answer: (a) 10√3
Hint:
The line through P (1, -5, 9) parallel to x = y = z is
\(\frac { x-1 }{1}\) = \(\frac { y+5 }{1}\) = \(\frac { z-9 }{1}\) …….. (1)
Any point on (1) is Q (1 + λ, -5 + λ, 9 + λ).
This lies on x – y + z = 5
⇒ 1 + λ + 5 – λ + 9 + λ = 5
⇒ λ = -10.
Q is (-9, -15, -1).
∴ |PQ| = \(\sqrt {(-9 – 1)^2 + (-15 + 5)^2 + (-1 – 9)^2}\)
= \(\sqrt {100+100+100}\)
= 10√3
Question 16.
An equation of a plane parallel to the plane x – 2y + 2z – 5 = 0 and at a unit distance from the origin is:
(a) x – 2y + 2z – 3 = 0
(b) x – 2y + 2z + 1 = 0
(c) x – 2y + 2z – 1 = 0
(d) x – 2y + 2z + 5 = 0.
Answer
Answer: (a) x – 2y + 2z – 3 = 0
Hint:
Any plane parallel to x – 2y + 2z – 5 = 0 is
x – 2y + 2z + k = 0 …….(1)
Its distance from the origin = 1
⇒ \(\frac { |0-0+0+k| }{\sqrt{1+4+4}}\) = 1
⇒ |k| = 3
⇒ k = ±3
Putting in (1), x – 2y + 2z – 3 = 0.
Question 17.
If the lines: \(\frac { x-2 }{1}\) = \(\frac { y-3 }{1}\) = \(\frac { z-4 }{-k}\) and \(\frac { x-1 }{k}\) = \(\frac { y-4 }{2}\) = \(\frac { z-5 }{1}\) are coplanar, then k can have:
(a) exactly one value
(b) exactly two values
(c) exactly three values
(d) any value.
Answer
Answer: (b) exactly two values
Hint:
The given parallel planes are:
\(\left|\begin{array}{rrr}
1 & -1 & -1 \\
1 & 1 & -k \\
k & 2 & 1
\end{array}\right|\) = 0
if (1)(1 + 2k) + (1)(1 + k²) + (-1)(2 – k) = 0
if 1 + 2k + 1 + k² – 2 + k = 0
if k² + 3k = 0 if k(k + 3) = 0
if k = 0, -3.
Hence, k can have exactly two values.
Question 18.
Distance between two parallel planes:
2x + y + 2z = 8 and 4x + 2y + 4z + 5 = 0 is
(a) \(\frac { 5 }{2}\)
(b) \(\frac { 7 }{2}\)
(c) \(\frac { 9 }{2}\)
(d) \(\frac { 3 }{2}\)
Answer
Answer: (b) \(\frac { 7 }{2}\)
Hint:
The given parallel planes are:
2x + y + 2z – 8 = 0
and 2x + y + 2z + \(\frac { 5 }{2}\) = 0.
∴ Distance between the planes
\(\frac { |8+5/2| }{\sqrt{4+1+4}}\) = \(\frac { 21 }{6}\) = \(\frac { 7 }{2}\)
Question 19.
The image of the line \(\frac { x-1 }{3}\) = \(\frac { y-3 }{1}\) = \(\frac { z-4 }{-5}\) in the plane:
2x – y + z + 3 = 0 is the line:
(a) \(\frac { x+3 }{-3}\) = \(\frac { y-5 }{-1}\) = \(\frac { z+2 }{5}\)
(b) \(\frac { x-3 }{3}\) = \(\frac { y+5 }{1}\) = \(\frac { z-2 }{-5}\)
(c) \(\frac { x-3 }{-3}\) = \(\frac { y+5 }{-1}\) = \(\frac { z-2 }{5}\)
(d) \(\frac { x+3 }{3}\) = \(\frac { y-5 }{1}\) = \(\frac { z-2 }{-5}\)
Answer
Answer: (d) \(\frac { x+3 }{3}\) = \(\frac { y-5 }{1}\) = \(\frac { z-2 }{-5}\)
Hint:
Since (3) (2) + (1) (-1) + (-5) (1) = 0
∴ the line is parallel to the plane.
Image of (1, 3, 4) is (-3, 5, 2).
∴ The required, image is
\(\frac { x+3 }{3}\) = \(\frac { y-5 }{1}\) = \(\frac { z-2 }{-5}\)
Question 20.
The distance of the point (1, 0, 2) from the point of intersection of the line
\(\frac { x-2 }{3}\) = \(\frac { y+1 }{4}\) = \(\frac { z-2 }{12}\) and flie plane x – y + z = 16 is
(a) 2\(\sqrt { 14 }\)
(b) 8
(c) 3\(\sqrt { 21 }\)
(d) 13.
Answer
Answer: (d) 13.
Hint:
Any point on the line is
(3k + 2, 4k – 1, 12k + 2).
This lies on the plane
⇒ 3k + 2 – 4k + 1 + 12k + 2 = 16
⇒ 11k = 11
⇒ k = 1.
∴ Point of intersection is (5, 3, 14).
∴ Its distance from (1, 0, 2)
\(\sqrt {(5 – 1)^2 + (3 – 0)^2 + (14 – 2)^2}\)
= \(\sqrt {16+9+144}\)
= \(\sqrt {169}\)
= 13
Question 21.
The equation of the plane containing the line: 2x – 5y + z = 3; x + y + 4z = 5 and parallel to the plane: x + 3y + 6z = 1 is:
(a) 2x + 6y+ 12z = 13
(b) x + 3y + 6z = – 7
(c) x + 3y + 6z = 7
(d) 2x + 6y – 12z = -13.
Answer
Answer: (c) x + 3y + 6z = 7
Hint:
Putting z = 0, 2x – 5y = 3 and x + y = 5.
Solving, x = 4, y = 1.
Let x + 3y + 6z = k be a plane parallel to given plane.
∴ 4 + 3 + 0 = k
⇒ k = 7
∴ Required, equation of the plane is x + 3y + 6z = 7
Question 22.
If the line \(\frac { x-3 }{2}\) = \(\frac { y+2 }{-1}\) = \(\frac { z+4 }{3}\) lies in the plane lx + my – z = 9,then l² + m² is equal to
(a) 18
(b) 5
(c) 2
(d) 26.
Answer
Answer: (c) 2
Hint:
Since the line \(\frac { x-3 }{2}\) = \(\frac { y+2 }{-1}\) = \(\frac { z+4 }{3}\) lies in the plane lx + my – z = 9,
∴ 3l – 2m + 4 = 9 and 2l – m – 3 = 0
Solving for l and m, we get:
l = 1 and m = -1
∴ l² + m² = 1 + 1 = 2.
Fill in the blanks
Question 1.
Direction-cosines of x-axis are ………………
Answer
Answer: < 1, 0, 0 >
Question 2.
Direction-cosines of y-axis are ………………
Answer
Answer: < 0, 1, 0 >.
Question 3.
Direction-cosines of z-axis are ………………..
Answer
Answer: < 0, 0, 1 >.
Question 4.
If a line makes angles 90°, 60° and θ with x, y and z-axis respectively, then acute θ = …………………
Answer
Answer: 30°.
Question 5.
Direction-cosines of the vector -2\(\hat i\) + \(\hat j\) – 5\(\hat k\) are …………………
Answer
Answer: < \(\frac { -2 }{\sqrt{30}}\), \(\frac { 1 }{\sqrt{30}}\), \(\frac { 5 }{\sqrt{30}}\) >
Question 6.
The points (1, 2, 7); (2, 6, 3); (3, 10, -1) are ………………..
Answer
Answer: collinear.
Question 7.
The value of ‘λ’ so that the lines
\(\frac { 1-x }{3}\) = \(\frac { 7y-14 }{λ}\) = \(\frac { z-3 }{2}\) and \(\frac { 7-7x }{3λ}\) = \(\frac { y-5 }{1}\) = \(\frac { 6-z }{5}\) are at right-angles is ………………..
Answer
Answer: 7
Question 8.
The sum of the intercepts cut off by the plane
\(\vec r\)(2\(\hat i\) + \(\hat j\) – \(\hat k\)) – 5 = 0 on the three axes is …………………..
Answer
Answer: 5/2
Question 9.
If α, ß, γ are direction-angles of a line, then:
cos 2α + cos 2ß + cos 2γ = ……………….
Answer
Answer: -1.
Question 10.
The equation of the plane with intercepts 2, 3 and 4 on the x, y and z-axis respectively is …………………..
Answer
Answer: \(\frac { x }{2}\) + \(\frac { y }{3}\) + \(\frac { z }{4}\) = 1
We hope you found this NCERT MCQ Questions for Class 12 Maths Chapter 11 Three Dimensional Geometry with Answers Pdf free download helpful. If you have any questions about CBSE Class 12 Maths Three Dimensional Geometry MCQs Multiple Choice Questions with Answers, please share them in the comment box below and we will get back to you at the earliest possible time.