Do you need some help in preparing for your upcoming Maths exam? We’ve compiled a list of MCQ Questions for Class 12 Maths with Answers to get you started with the subject, Vector Algebra Class 12 MCQs Questions with Answers. You can download NCERT MCQ Questions for Class 12 Maths Chapter 10 Vector Algebra with Answers Pdf free download and learn how smart students improve problem-solving skills well ahead. So, ace up your preparation with Class 12 Maths Chapter 10 Vector Algebra Objective Questions.
Vector Algebra Class 12 MCQs Questions with Answers
Don’t forget to practice the multitude of MCQ Questions on Vector Algebra Class 12 with answers so you can apply your skills during the exam.
Question 1.
In ΔABC, which of the following is not true?
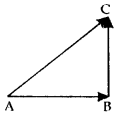
(a) \(\vec { AB}\) + \(\vec { BC}\) + \(\vec { CA}\) = \(\vec { 0}\)
(b) \(\vec { AB}\) + \(\vec { BC}\) – \(\vec { AC}\) = \(\vec { 0}\)
(c) \(\vec { AB}\) + \(\vec { BC}\) – \(\vec { CA}\) = \(\vec { 0}\)
(d) \(\vec { AB}\) – \(\vec { CB}\) + \(\vec { CA}\) = \(\vec { 0}\)
Answer
Answer: (c) \(\vec { AB}\) + \(\vec { BC}\) – \(\vec { CA}\) = \(\vec { 0}\)
Question 2.
If \(\vec a\) and \(\vec b\) are two collinear vectors, then which of the following are incorrect:
(a) \(\vec b\) = λ\(\vec a\) tor some scalar λ.
(b) \(\vec a\) = ±\(\vec b\)
(c) the respective components of \(\vec a\) and \(\vec b\) are proportional
(d) both the vectors \(\vec a\) and \(\vec b\) have the same direction, but different magnitudes.
Answer
Answer: (d) both the vectors \(\vec a\) and \(\vec b\) have the same direction, but different magnitudes.
Question 3.
If a is a non-zero vector of magnitude ‘a’ and λa non-zero scalar, then λ\(\vec a\) is unit vector if:
(a) λ = 1
(b) λ = -1
(c) a = |λ|
(d) a = \(\frac { 1 }{|λ|}\)
Answer
Answer: (d) a = \(\frac { 1 }{|λ|}\)
Question 4.
Let λ be any non-zero scalar. Then for what possible values of x, y and z given below, the vectors 2\(\hat i\) – 3\(\hat j\) + 4\(\hat k\) and x\(\hat i\) – y\(\hat j\) + z\(\hat k\) are perpendicular:
(a) x = 2λ. y = λ, z = λ
(b) x = λ, y = 2λ, z = -λ
(c) x = -λ, y = 2λ, z = λ
(d) x = -λ, y = -2λ, z = λ.
Answer
Answer: (c) x = -λ, y = 2λ, z = λ
Question 5.
Let the vectors \(\vec a\) and \(\vec b\) be such that |\(\vec a\)| = 3 and |\(\vec b\)| = \(\frac { √2 }{3}\), then \(\vec a\) × \(\vec b\) is a unit vector if the angle between \(\vec a\) and \(\vec b\) is:
(a) \(\frac { π }{6}\)
(b) \(\frac { π }{4}\)
(c) \(\frac { π }{3}\)
(d) \(\frac { π }{2}\)
Answer
Answer: (b) \(\frac { π }{4}\)
Question 6.
Area of a rectangle having vertices
A(-\(\hat i\) + \(\frac { 1 }{2}\) \(\hat j\) + 4\(\hat k\)),
B(\(\hat i\) + \(\frac { 1 }{2}\) \(\hat j\) + 4\(\hat k\)),
C(\(\hat i\) – \(\frac { 1 }{2}\) \(\hat j\) + 4\(\hat k\)),
D(-\(\hat i\) – \(\frac { 1 }{2}\) \(\hat j\) + 4\(\hat k\)) is
(a) \(\frac { 1 }{2}\) square unit
(b) 1 square unit
(c) 2 square units
(d) 4 square units.
Answer
Answer: (c) 2 square units
Question 7.
If θ is the angle between two vectors \(\vec a\), \(\vec b\), then \(\vec a\).\(\vec b\) ≥ 0 only when
(a) 0 < θ < \(\frac { π }{2}\)
(b) 0 ≤ θ ≤ \(\frac { π }{2}\)
(c) 0 < θ < π
(d) 0 ≤ θ ≤ π
Answer
Answer: (b) 0 ≤ θ ≤ \(\frac { π }{2}\)
Question 8.
Let \(\vec a\) and \(\vec b\) be two unit vectors and 6 is the angle between them. Then \(\vec a\) + \(\vec b\) is a unit vector if:
(a) θ = \(\frac { π }{4}\)
(b) θ = \(\frac { π }{3}\)
(c) θ = \(\frac { π }{2}\)
(d) θ = \(\frac { 2π }{3}\)
Answer
Answer: (d) θ = \(\frac { 2π }{3}\)
Question 9.
If {\(\hat i\), \(\hat j\), \(\hat k\)} are the usual three perpendicular unit vectors, then the value of:
\(\hat i\).(\(\hat j\) × \(\hat k\)) + \(\hat j\).(\(\hat i\) × \(\hat k\)) + \(\hat k\).(\(\hat i\) × \(\hat j\)) is
(a) 0
(b) -1
(c) 1
(d) 3
Answer
Answer: (d) 3
Question 10.
If θ is the angle between two vectors \(\vec a\) and \(\vec b\), then |\(\vec a\).\(\vec b\)| = |\(\vec a\) × \(\vec b\)| when θ is equal to:
(a) 0
(b) \(\frac { π }{4}\)
(c) \(\frac { π }{2}\)
(d) π
Answer
Answer: (b) \(\frac { π }{4}\)
Question 11.
The area of the triangle whose adjacent sides are
\(\vec a\) = 3\(\hat i\) + \(\hat j\) + 4\(\hat k\) and \(\vec b\) = \(\hat i\) – \(\hat j\) + \(\hat k\) is
(a) \(\frac { 1 }{2}\) \(\sqrt{ 42 }\)
(b) 42
(c) \(\sqrt{ 42 }\)
(d) \(\sqrt{ 21 }\)
Answer
Answer: (a) \(\frac { 1 }{2}\) \(\sqrt{ 42 }\)
Question 12.
The magnitude of the vector 6\(\hat i\) + 2\(\hat j\) + 3\(\hat k\) is
(a) 5
(b) 7
(c) 12
(d) 1.
Answer
Answer: (b) 7
Question 13.
The vector with initial point P (2, -3, 5) and terminal point Q (3, -4, 7) is
(a) \(\hat i\) – \(\hat j\) + 2\(\hat k\)
(b) 5\(\hat i\) – 7\(\hat j\) + 12\(\hat k\)
(c) –\(\hat i\) + \(\hat j\) – 2\(\hat k\)
(d) None of these.
Answer
Answer: (a) \(\hat i\) – \(\hat j\) + 2\(\hat k\)
Question 14.
The angle between the vectors \(\hat i\) – \(\hat j\) and \(\hat j\) – \(\hat k\) is
(a) \(\frac { π }{3}\)
(b) \(\frac { 2π }{3}\)
(c) –\(\frac { π }{3}\)
(d) \(\frac { 5π }{6}\)
Answer
Answer: (b) \(\frac { 2π }{3}\)
Question 15.
The value of ‘λ’ for which the two vectors:
2\(\hat i\) – \(\hat j\) + 2\(\hat k\) and 3\(\hat i\) + λ\(\hat j\) + \(\hat k\) are perpendicular is
(a) 2
(b) 4
(c) 6
(d) 8.
Answer
Answer: (d) 8.
Question 16.
If |\(\vec a\)| = 8, |\(\vec b\)| = 3 and |\(\vec a\) × \(\vec b\)|= 12, then value of \(\vec a\).\(\vec b\) is
(a) 6√3
(b) 8√3
(c) 12√3
(d) None of these.
Answer
Answer: (c) 12√3
Question 17.
The non-zero vectors \(\vec a\), \(\vec b\) and \(\vec c\) are related by \(\vec a\) = 8\(\vec b\) and \(\vec c\) = -7\(\vec b\). Then the angle between \(\vec a\) and \(\vec c\) is
(a) π
(b) 0
(c) \(\frac { π }{4}\)
(d) \(\frac { π }{2}\)
Answer
Answer: (a) π
Hint:
\(\vec a\) = 8\(\vec b\) and \(\vec c\) = -7\(\vec b\)
Clearly \(\vec a\) and \(\vec b\) are parallel and \(\vec b\) and \(\vec c\) are anti-parallel.
∴ \(\vec a\) and \(\vec c\) are anti-parallel.
Hence, angle between \(\vec a\) and \(\vec c\) is π.
Question 18.
If the vectors \(\vec a\) = \(\hat i\) – \(\hat j\) + 2\(\hat k\), \(\vec b\) = 2\(\hat i\) + 4\(\hat j\) + \(\hat k\) and \(\vec c\) = λ\(\hat i\) + \(\hat j\) + µ\(\hat k\) are mutually orthogonal, then (λ, µ) =
(a) (-3, 2)
(b) (2, -3)
(c) (-2, 3)
(d)(3, -2).
Answer
Answer: (a) (-3, 2)
Hint:
\(\vec a\), \(\vec b\) and \(\vec c\) are mutually orthogonal
⇒ \(\vec b\).\(\vec c\) = 0 and \(\vec a\).\(\vec c\) = 0
⇒ (2\(\hat i\) + 4\(\hat j\) + \(\hat k\)). (λ\(\hat i\) + \(\hat j\) + µ\(\hat i\)) = 0
⇒ 2λ + 4 + µ = 0
⇒ 2λ + µ = -4 …………(1)
and (\(\hat i\) – \(\hat j\) + 2\(\hat k\)).(λ\(\hat i\) + \(\hat j\) + µ\(\hat k\)) = 0
⇒ λ – 1 + 2µ = 0
⇒ λ + 2µ = 1 ………….. (2)
Solving (1) and (2),
λ = -3 and µ = 2.
Question 19.
If (2\(\hat i\) + 6\(\hat j\) + 27\(\hat k\)) × (\(\hat i\) + p\(\hat j\) + q\(\hat k\)) = \(\vec 0\), then the values ofp and q are?
(a) p = 6, q = 27
(b) p = 3, q = \(\frac { 27 }{2}\)
(c) p = 6, q = \(\frac { 27 }{2}\)
(d) p = 3, q = 27.
Answer
Answer: (b) p = 3, q = \(\frac { 27 }{2}\)
Hint:
(2\(\hat i\) + 6\(\hat j\) + 27\(\hat k\)) × (\(\hat i\) + p\(\hat j\) + q\(\hat k\))
\(\left[\begin{array}{ccc}
\hat{i} & \hat{j} & \hat{k} \\
2 & 6 & 27 \\
1 & p & q
\end{array}\right]\)
By the question,
\(\hat i\) (6q – 27p) –\(\hat j\) (2q – 27) +\(\hat k\) (2p – 6) = \(\vec 0\)
⇒ 6q – 27p = 0 ⇒ 2q – 9p = 0
2q – 27 = 0 ⇒ q = \(\frac { 27 }{2}\)
and 2p – 6 = 0 ⇒ p = 3.
Hence, p = 3 and q = \(\frac { 27 }{2}\).
Question 20.
If the vectors \(\bar { AB }\) = 3\(\hat i\) + 4\(\hat k\) and \(\bar { AC }\) = 5\(\hat i\) – 2\(\hat j\) + 4\(\hat k\) are the sides ofa triangle ABC, then the length of the median through A is
(a) \(\sqrt {72}\)
(b) \(\sqrt {33}\)
(c) \(\sqrt {45}\)
(d) \(\sqrt {18}\)
Answer
Answer: (b) \(\sqrt {33}\)
Hint:
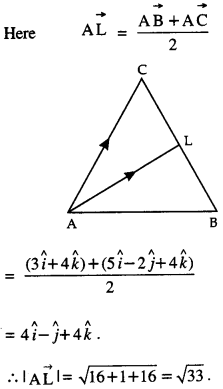
Question 21.
If [\(\vec a\) × \(\vec b\) \(\vec b\) × \(\vec c\) \(\vec c\) × \(\vec a\)] = λ [\(\vec a\) \(\vec b\) \(\vec c\)]², then λ is equal to
(a) 3
(b) 0
(c) 1
(d) 2.
Answer
Answer: (c) 1
Hint:
As usual, we will have:
[\(\vec a\) × \(\vec b\) \(\vec b\) × \(\vec c\) \(\vec c\) × \(\vec a\)] = [\(\vec a\) \(\vec b\) \(\vec c\)]²
Given:
[\(\vec a\) × \(\vec b\) \(\vec b\) × \(\vec c\) \(\vec c\) × \(\vec a\)] = [\(\vec a\) \(\vec b\) \(\vec c\)]²
Hence, λ = 1.
Question 22.
Let \(\vec a\), \(\vec b\) and \(\vec c\) be three unit vectors such that:
\(\vec a\) × (\(\vec b\) × \(\vec c\)) = \(\frac { √3 }{2}\) (\(\vec b\) + \(\vec c\))
If \(\vec b\) is not parallel to \(\vec c\), then the angle between \(\vec a\) and \(\vec b\) is:
(a) \(\frac { π }{2}\)
(b) \(\frac { 2π }{3}\)
(c) \(\frac { 5π }{6}\)
(d) \(\frac { 3π }{4}\)
Answer
Answer: (c) \(\frac { 5π }{6}\)
Hint:
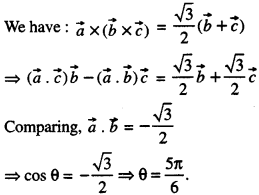
Fill in the blanks
Question 1.
The magnitude of projection of (2\(\hat i\) – \(\hat j\) + \(\hat k\))
on (\(\hat i\) – 2\(\hat j\) + 2\(\hat k\)) is ……………….
Answer
Answer: 2 units.
Question 2.
Vector of magnitude 5 units and in the direction opposite to 2\(\hat i\) + 3\(\hat j\) – 6\(\hat k\) is ……………..
Answer
Answer: \(\frac { 5 }{7}\) (-2\(\hat i\) – 3\(\hat j\) + 6\(\hat k\))
Question 3.
The sum of the vectors
\(\vec a\) = \(\hat i\) – 2\(\hat j\) + \(\hat k\), \(\vec b\) = -2\(\hat i\) + 4\(\hat j\) + 5\(\hat k\) and \(\vec c\) = \(\hat i\) – 6\(\hat j\) – 7\(\hat k\) is ……………….
Answer
Answer: -4\(\hat i\) – \(\hat k\)
Question 4.
The value of ‘a’ when the vectors:
2\(\hat i\) – 3\(\hat j\) + 4\(\hat k\) and a\(\hat i\) + b\(\hat j\) – 8\(\hat k\) are collinear is ……………….
Answer
Answer: -4
Question 5.
If \(\vec a\) = 2\(\hat i\) + \(\hat j\) – 2\(\hat k\), then |\(\vec a\)| = ……………….
Answer
Answer: 3.
Question 6.
If \(\vec a\) is a unit vector and (\(\vec x\) – \(\vec a\)).(\(\vec x\) + \(\vec a\)) = 8, then |\(\vec x\)| = …………….
Answer
Answer: 3.
Question 7.
(\(\hat i\) × \(\hat j\)).\(\hat k\) + \(\hat i\).\(\hat j\) = ……………..
Answer
Answer: 1.
Question 8.
The value of ‘λ’ of (2\(\hat i\) + 6\(\hat j\) + 14\(\hat k\)) × (\(\hat i\) – λ\(\hat j\) + 7\(\hat k\)) = \(\vec 0\) is ……………….
Answer
Answer: -3
Question 9.
If any two vectors \(\vec a\), \(\vec b\), \(\vec c\) are parallel, then [\(\vec a\). \(\vec b\). \(\vec c\)] = …………………
Answer
Answer: 0.
Question 10.
The value of ‘λ’ such that the vectors:
3\(\hat i\) + \(\hat j\) + 5\(\hat k\), \(\hat i\) + 2\(\hat j\) – 3\(\hat k\) and 2\(\hat i\) – \(\hat j\) + \(\hat k\) are coplanar is ………………..
Answer
Answer: -4.
We hope you found this NCERT MCQ Questions for Class 12 Maths Chapter 10 Vector Algebra with Answers Pdf free download helpful. If you have any questions about CBSE Class 12 Maths Vector Algebra MCQs Multiple Choice Questions with Answers, please share them in the comment box below and we will get back to you at the earliest possible time.